文本去重之MinHash算法
1.概述
Jaccard index是用来计算相似性,也就是距离的一种度量标准。假如有集合A、B,那么,
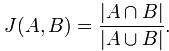
那么对集合A、B,hmin(A) = hmin(B)成立的条件是A ∪ B 中具有最小哈希值的元素也在 ∩ B中。这里
有一个假设,h(x)是一个良好的哈希函数,它具有很好的均匀性,能够把不同元素映射成不同的整数。
所以有,Pr[hmin(A) = hmin(B)] = J(A,B),即集合A和B的相似度为集合A、B经过hash后最小哈希值相
等的概率。
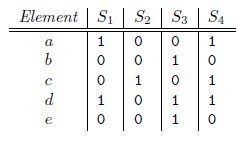
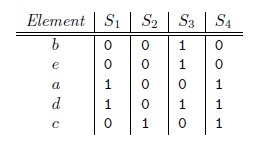
文本去重之MinHash算法的更多相关文章
- 文本去重之MinHash算法——就是多个hash函数对items计算特征值,然后取最小的计算相似度
来源:http://my.oschina.net/pathenon/blog/65210 1.概述 跟SimHash一样,MinHash也是LSH的一种,可以用来快速估算两个集合的相似度.Mi ...
- 文本去重之SimHash算法
文本去重之SimHash算法 - pathenon的个人页面 - 开源中国社区 文本去重之SimHash算法
- 文本相似性计算--MinHash和LSH算法
给定N个集合,从中找到相似的集合对,如何实现呢?直观的方法是比较任意两个集合.那么可以十分精确的找到每一对相似的集合,但是时间复杂度是O(n2).此外,假如,N个集合中只有少数几对集合相似,绝大多数集 ...
- [Algorithm] 使用SimHash进行海量文本去重
在之前的两篇博文分别介绍了常用的hash方法([Data Structure & Algorithm] Hash那点事儿)以及局部敏感hash算法([Algorithm] 局部敏感哈希算法(L ...
- 使用SimHash进行海量文本去重[转载]
阅读目录 1. SimHash与传统hash函数的区别 2. SimHash算法思想 3. SimHash流程实现 4. SimHash签名距离计算 5. SimHash存储和索引 6. SimHas ...
- 使用SimHash进行海量文本去重[转]
阅读目录 1. SimHash与传统hash函数的区别 2. SimHash算法思想 3. SimHash流程实现 4. SimHash签名距离计算 5. SimHash存储和索引 6. SimHas ...
- 使用SimHash进行海量文本去重
阅读目录 1. SimHash与传统hash函数的区别 2. SimHash算法思想 3. SimHash流程实现 4. SimHash签名距离计算 5. SimHash存储和索引 6. SimHas ...
- 海量数据去重之SimHash算法简介和应用
SimHash是什么 SimHash是Google在2007年发表的论文<Detecting Near-Duplicates for Web Crawling >中提到的一种指纹生成算法或 ...
- 初识【Windows API】--文本去重
最近学习操作系统中,老师布置了一个作业,运用系统调用函数删除文件夹下两个重复文本类文件,Linux玩不动,于是就只能在Windows下进行了. 看了一下介绍Windows API的博客: 点击打开 基 ...
随机推荐
- MQ集群测试环境搭建(多节点负载均衡,共享一个kahaDB文件(nas方式))
1. os ubuntu12.04 基础环境准备 干掉不好用的vim重新装 sudo apt-get remove vim-common sudo apt-get install vim 如果需要使用 ...
- [原创]java WEB学习笔记77:Hibernate学习之路---Hibernate 版本 helloword 与 解析,.环境搭建,hibernate.cfg.xml文件及参数说明,持久化类,对象-关系映射文件.hbm.xml,Hibernate API (Configuration 类,SessionFactory 接口,Session 接口,Transaction(事务))
本博客的目的:①总结自己的学习过程,相当于学习笔记 ②将自己的经验分享给大家,相互学习,互相交流,不可商用 内容难免出现问题,欢迎指正,交流,探讨,可以留言,也可以通过以下方式联系. 本人互联网技术爱 ...
- [原创]java WEB学习笔记72:Struts2 学习之路-- 文件的上传下载,及上传下载相关问题
本博客的目的:①总结自己的学习过程,相当于学习笔记 ②将自己的经验分享给大家,相互学习,互相交流,不可商用 内容难免出现问题,欢迎指正,交流,探讨,可以留言,也可以通过以下方式联系. 本人互联网技术爱 ...
- UML: 协作图
摘自http://www.umlonline.org/school/thread-38-1-1.html UML1.1时,协作图英文名字叫:Collaboration Diagram,UML2.0时, ...
- javaapi中的排序
有的时候需要对数组里的element进行排序.当然可以自己编写合适的排序方法,但既然java包里有自带的Arrays.sort排序方法,在 数组元素比较少的时候为何不用? Sorting an Arr ...
- bzoj4448 [Scoi2015]情报传递
第一问不解释,对于第二问的处理,可以使用cdq分治,假设分治的询问区间是[L,R],那么我们对于标号在[L,mid]的修改操作赋予一个权值,因为在当前[L,R]中[L,mid]的修改操作只会对[mid ...
- CCF真题之网络延时
201503-4 问题描述 给定一个公司的网络,由n台交换机和m台终端电脑组成,交换机与交换机.交换机与电脑之间使用网络连接.交换机按层级设置,编号为1的交换机为根交换机,层级为1.其他的交换机都连接 ...
- fackbook的Fresco的多种图片加载方法以及解码过程
上篇文章中我们提到了图片加载其实是用了三条线程,如果没看过的同学可以先了解下这里. fackbook的Fresco的Image Pipeline以及自身的缓存机制 那么今天我们就来探索一下如何在代码中 ...
- paper 76:膨胀、腐蚀、开、闭运算——数字图像处理中的形态学
膨胀.腐蚀.开.闭运算是数学形态学最基本的变换.本文主要针对二值图像的形态学膨胀:把二值图像各1像素连接成分的边界扩大一层(填充边缘或0像素内部的孔):腐蚀:把二值图像各1像素连接成分的边界点去掉从而 ...
- paper 17 : 机器学习算法思想简单梳理
前言: 本文总结的常见机器学习算法(主要是一些常规分类器)大概流程和主要思想. 朴素贝叶斯: 有以下几个地方需要注意: 1. 如果给出的特征向量长度可能不同,这是需要归一化为通长度的向量(这里以文本分 ...
