使用kd-tree加速k-means

0.目录

• 前置知识
• 思路介绍
• 详述
  • 1 确定h的中心点
  • 2 算法步骤
• java实现

1.前置知识

本文内容基于《Accelerating exact k-means algorithms with geometric reasoning》
KDTree
k-means

2.思路介绍

k-means算法在初始化中心点后C通过以下迭代步骤得到局部最优解：

  a.将数据集D中的点x赋给距离最近的中心点

  b.在每个聚类中，重新计算中心点

传统算法中，a步需要计算n*k个距离（n为D的大小，k为聚类个数），b步需要相加n个数据点

而在KDTree中，每个非叶子节点，都存储了其包含的数据的数据范围信息h。

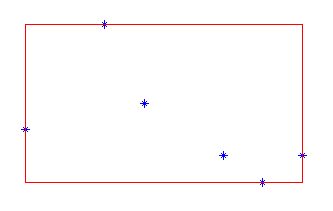二维空间中的h可以使用矩形来表示 图中*为点，红色矩形为数据范围h

a.
如果通过范围信息，能判断节点中数据都属于中心点c，则能省去节点中数据到中心点距离的计算

    
如果能判断h中数据都不属于某中心点c，则能省去节点中数据到中心点c距离的计算

  b.
当知道节点中数据全部属于c，能将h中事先加好的统计量直接加到c的统计量中

3.详述

3.1
确定h的中心点（h中所有数据都离这个中心点近而离其他中心点远）

KDTree的节点中存储的Max(各维度上的最大值)和Min(各维度上的最小值)确定了节点中数据的范围

中心点有(c1,c2,...,ck)

a.
判断是否可能存在

  计算各中心点到h的最小距离（参考KDTree最近邻查找，第5步） d(ci,h)

  如果存在一个最小距离，则这个ci可能是h的中心点（还需要进一步判断）

  若存在不止一个最小距离，则h的中心点不存在，需要将h分割为更小（在h的左右树上）后查找

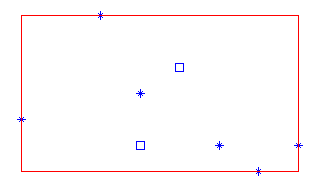正方形表示的点都在h的内部 所以他们到h的最小距离相同，都为0 此h不存在中心点

b.
进一步判断，ci是否为中心点

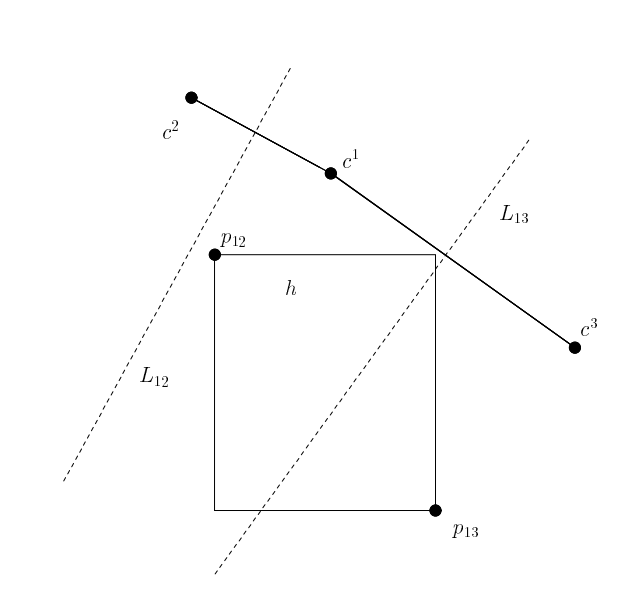	L12为c1和c2连线的中位线，h全部落在c1一边, 所以h中的全部点离c1比离c2近，称c1优于c2 而对于c1和c3来说，h有一部分落在c1，有一部分落在c3 c1不优于c3
判断c1是否优于c3: 取向量v=(c3-c1),找到点p属于h，使<v,p>内积最大 v各维度正负情况(+,-)，则p在x轴上尽可能大，y轴上尽可能小，取到p13 p13离c3近，所以c1不优于c3

如果ci在优于其他点，则可以判定ci即为h的中心点；否则ci不是h的中心点;
  虽然ci不是h的中心点，但是得到的信息，如ci优于c2，能将c2从h的子树的中心点候选列表中排除

3.2
算法步骤

KDTree中每个非叶子节点特殊属性：
sumOfPoints：m维向量（m是数据的维度），其i维度的值为节点中数据第i维的和
n：节点中数据的个数

输入：KDTree,C 包括中心点(c1,c2,...,ck)

输出：CNEW 新的k个中心点

node=KDTree.root
centers=k*m的数组//每行存储属于这个中心点的数据的和
datacount=k*1的数组//存储属于这个中心点的数据个数

UPDATE(node,C)：
IF node为叶子节点
  遍历计算得到离node最近的节点ct
  centers[t]+=node.value;
  datacount[t]+=1;
  RETURN;

FOR(ci in C)  计算d(ci,node.h)
IF 有多个最小的d(ci,node.h)
  UPDATE(node.left,C);
  UPDATE(node.right,C);
  RETURN;
//假设d(ci,node.h)最小的是ct
CTOVER=[]//存储劣于ct的
FOR(ci in C(除了ct))  IF(ct 优于 ci) CTOVER.ADD(ci)
IF(LEN(CTOVER)=LEN(C)-1)//ct优于其他的中心点
  centers[t]+=node.sumOfPoints;
  datacount[t]+=node.n;
  RETURN;
CT=(ci in C 且 ci not in CTOVER)//排除比ct差的中心点
UPDATE(node.left,CT);
UPDATE(node.right,CT);
RETURN;

4.java实现

a.用下列matlab方法生成测试数据

#centers为中心点个数，dimention为数据维度，persize为每个中心点包含的数据量
function cdata(centers,dimention,persize)

d=zeros(centers*persize,dimention);
sigma=eye(dimention);
for i=1:centers
    mu=randi(20,1,dimention);
    d(((i-1)*persize+1):i*persize,:)=mvnrnd(mu,sigma,persize);
end
dlmwrite('d.txt',d,'delimiter','\t','precision','%10.4f')
end

b.kdtree

package cc;
import java.util.ArrayList;
import java.util.HashMap;

public class MRKDTree {

    private Node mrkdtree;

    private class Node{
        //分割的维度
        int partitionDimention;
        //分割的值
        double partitionValue;
        //如果为非叶子节点，该属性为空
        //否则为数据
        double[] value;
        //是否为叶子
        boolean isLeaf=false;
        //左树
        Node left;
        //右树
        Node right;
        //每个维度的最小值
        double[] min;
        //每个维度的最大值
        double[] max;

        double[] sumOfPoints;
        int n;
    }

    private static class UtilZ{
        /**
         * 计算给定维度的方差
         * @param data 数据
         * @param dimention 维度
         * @return 方差
         */
        static double variance(ArrayList<double[]> data,int dimention){
            double vsum = 0;
            double sum = 0;
            for(double[] d:data){
                sum+=d[dimention];
                vsum+=d[dimention]*d[dimention];
            }
            int n = data.size();
            return vsum/n-Math.pow(sum/n, 2);
        }
        /**
         * 取排序后的中间位置数值
         * @param data 数据
         * @param dimention 维度
         * @return
         */
        static double median(ArrayList<double[]> data,int dimention){
            double[] d =new double[data.size()];
            int i=0;
            for(double[] k:data){
                d[i++]=k[dimention];
            }
            return median(d);
        }

        private static double median(double[] a){
            int n=a.length;
            int L = 0;
            int R = n - 1;
            int k = n / 2;
            int i;
            int j;
            while (L < R) {
                double x = a[k];
                i = L;
                j = R;
                do {
                    while (a[i] < x)
                        i++;
                    while (x < a[j])
                        j--;
                    if (i <= j) {
                        double t = a[i];
                        a[i] = a[j];
                        a[j] = t;
                        i++;
                        j--;
                    }
                } while (i <= j);
                if (j < k)
                    L = i;
                if (k < i)
                    R = j;
            }
            return a[k];
        }

        static double[][] maxmin(ArrayList<double[]> data,int dimentions){
            double[][] mm = new double[2][dimentions];
            //初始化 第一行为min，第二行为max
            for(int i=0;i<dimentions;i++){
                mm[0][i]=mm[1][i]=data.get(0)[i];
                for(int j=1;j<data.size();j++){
                    double[] d = data.get(j);
                    if(d[i]<mm[0][i]){
                        mm[0][i]=d[i];
                    }else if(d[i]>mm[1][i]){
                        mm[1][i]=d[i];
                    }
                }
            }
            return mm;
        }

        static double distance(double[] a,double[] b){
            double sum = 0;
            for(int i=0;i<a.length;i++){
                sum+=Math.pow(a[i]-b[i], 2);
            }
            return sum;
        }

        /**
         * 在max和min表示的超矩形中的点和点a的最小距离
         * @param a 点a
         * @param max 超矩形各个维度的最大值
         * @param min 超矩形各个维度的最小值
         * @return 超矩形中的点和点a的最小距离
         */
        static double mindistance(double[] a,double[] max,double[] min){
            double sum = 0;
            for(int i=0;i<a.length;i++){
                if(a[i]>max[i])
                    sum += Math.pow(a[i]-max[i], 2);
                else if (a[i]<min[i]) {
                    sum += Math.pow(min[i]-a[i], 2);
                }
            }

            return sum;
        }

        public static double[] sumOfPoints(ArrayList<double[]> data,
                int dimentions) {
            double[] res = new double[dimentions];
            for(double[] d:data){
                for(int i=0;i<dimentions;i++){
                    res[i]+=d[i];
                }
            }
            return res;
        }
        /**
         * 判断centerd是否在h上优于c
         * @param centerd
         * @param c
         * @param max
         * @param min
         * @return
         */
        public static boolean isOver(double[] center, double[] c,
                double[] max, double[] min) {
            double discenter = 0;
            double disc = 0;
            for(int i=0;i<c.length;i++){
                if(c[i]-center[i]>0){
                    disc+=Math.pow(max[i]-c[i],2);
                    discenter+=Math.pow(max[i]-center[i],2);
                }else if(c[i]-center[i]<0) {
                    disc+=Math.pow(min[i]-c[i],2);
                    discenter+=Math.pow(min[i]-center[i],2);
                }

            }
            return discenter<disc;
        }
    }

    private MRKDTree() {}
    /**
     * 构建树
     * @param input 输入
     * @return KDTree树
     */
    public static MRKDTree build(double[][] input){
        int n = input.length;
        int m = input[0].length;

        ArrayList<double[]> data =new ArrayList<double[]>(n);
        for(int i=0;i<n;i++){
            double[] d = new double[m];
            for(int j=0;j<m;j++)
                d[j]=input[i][j];
            data.add(d);
        }

        MRKDTree tree = new MRKDTree();
        tree.mrkdtree = tree.new Node();
        tree.buildDetail(tree.mrkdtree, data, m,0);

        return tree;
    }
    /**
     * 循环构建树
     * @param node 节点
     * @param data 数据
     * @param dimentions 数据的维度
     */
    private void buildDetail(Node node,ArrayList<double[]> data,int dimentions,int lv){
        if(data.size()==1){
            node.isLeaf=true;
            node.value=data.get(0);
            return;
        }

        //选择方差最大的维度
        /*
        node.partitionDimention=-1;
        double var = -1;
        double tmpvar;
        for(int i=0;i<dimentions;i++){
            tmpvar=UtilZ.variance(data, i);
            if (tmpvar>var){
                var = tmpvar;
                node.partitionDimention = i;
            }
        }
        //如果方差=0，表示所有数据都相同，判定为叶子节点
        if(var<1e-10){
            node.isLeaf=true;
            node.value=data.get(0);
            return;
        }
        */
        double[][] maxmin=UtilZ.maxmin(data, dimentions);

        node.min = maxmin[0];
        node.max = maxmin[1];

        //选取方差大的维度，会需要很长时间
        //改成使用选取数据范围最大的维度
        //这样构建kdtree的速度会变快，但是在kmean更新中心点会变慢
        boolean isleaf = true;
        for(int i=0;i<node.min.length;i++)
            if(node.min[i]!=node.max[i]){
                isleaf=false;
                break;
            }

        if(isleaf){
            node.isLeaf=true;
            node.value=data.get(0);
            return;
        }

        node.partitionDimention=-1;
        double diff = -1;
        double tmpdiff;
        for(int i=0;i<dimentions;i++){
            tmpdiff=node.max[i]-node.min[i];
            if (tmpdiff>diff){
                diff = tmpdiff;
                node.partitionDimention = i;
            }
        }

        node.sumOfPoints = UtilZ.sumOfPoints(data,dimentions);
        node.n = data.size();

        //选择分割的值
        node.partitionValue=UtilZ.median(data, node.partitionDimention);
        if(node.partitionValue==node.min[node.partitionDimention]){
            node.partitionValue+=1e-5;
        }

        int size = (int)(data.size()*0.55);
        ArrayList<double[]> left = new ArrayList<double[]>(size);
        ArrayList<double[]> right = new ArrayList<double[]>(size);

        for(double[] d:data){
            if (d[node.partitionDimention]<node.partitionValue) {
                left.add(d);
            }else {
                right.add(d);
            }
        }

        Node leftnode = new Node();
        Node rightnode = new Node();
        node.left=leftnode;
        node.right=rightnode;
        buildDetail(leftnode, left, dimentions,lv+1);
        buildDetail(rightnode, right, dimentions,lv+1);
    }

    public double[][] updateCentroids(double[][] cs){
        int k = cs.length;
        int m = cs[0].length;
        double[][] entroids = new double[k][m];
        int[] datacount = new int[k];
        HashMap<Integer, double[]> cscopy = new HashMap<Integer, double[]>();
        for(int i=0;i<k;i++)
            cscopy.put(i, cs[i]);

        updateCentroidsDetail(mrkdtree,cscopy,entroids,datacount,k,m);
        double[][] csnew = new double[k][m];
        for(int i=0;i<k;i++){
            for(int j=0;j<m;j++){
                csnew[i][j]=entroids[i][j]/datacount[i];
            }
        }

        return csnew;
    }

    private void updateCentroidsDetail(Node node,
            HashMap<Integer, double[]> cs, double[][] entroids,
            int[] datacount,int k,int m) {
        //如果是叶子节点
        if(node.isLeaf){
            double[] v=node.value;
            double dis=Double.MAX_VALUE;
            double tdis;
            int index = -1;
            //找到所属的中心点
            for(Integer i: cs.keySet()){
                double[] c = cs.get(i);
                tdis = UtilZ.distance(c, v);
                if(tdis<dis){
                    dis=tdis;
                    index=i;
                }
            }

            //更新统计信息
            datacount[index]++;
            for(int i=0;i<m;i++){
                entroids[index][i]+=v[i];
            }
            return;
        }

        double[] stack = new double[k];
        int stackpoint = 0;
        int center=0;
        double tdis;
        for(Integer i: cs.keySet()){
            double[] c = cs.get(i);
            tdis = UtilZ.mindistance(c, node.max, node.min);
            if(stackpoint==0){
                stack[stackpoint++]=tdis;
                center=i;
            }else if (tdis<stack[stackpoint-1]) {
                stackpoint=1;
                stack[0]=tdis;
                center=i;
            }else if (tdis==stack[stackpoint-1]) {
                stack[stackpoint++]=tdis;
            }

        }
        //stackpoint>1，说明有多个最小值，不存在中心点
        if(stackpoint!=1){
            updateCentroidsDetail(node.left, cs, entroids, datacount, k, m);
            updateCentroidsDetail(node.right, cs, entroids, datacount, k, m);
            return;
        }

        HashMap<Integer, Boolean> ctover = new HashMap<Integer, Boolean>();
        double[] centerd = cs.get(center);
        for(Integer i: cs.keySet()){
            if(i==center) continue;
            double[] c = cs.get(i);
            if(UtilZ.isOver(centerd,c,node.max,node.min)){
                ctover.put(i, true);
            }
        }

        if(ctover.size()==cs.size()-1){
            //此时中心点即为center，更新信息
            datacount[center]+=node.n;
            for(int i=0;i<m;i++){
                entroids[center][i]+=node.sumOfPoints[i];
            }
            return;
        }

        //将其比center差的中心点排除
        HashMap<Integer, double[]> csnew = new HashMap<Integer, double[]>();
        for(Integer i:cs.keySet()){
            if(!ctover.containsKey(i))
                csnew.put(i, cs.get(i));
        }

        updateCentroidsDetail(node.left, csnew, entroids, datacount, k, m);
        updateCentroidsDetail(node.right, csnew, entroids, datacount, k, m);
    }
}

c.kmeans

import cc.MRKDTree;

public class KMeans {
    private double[][] centroids;

    private KMeans(){}

    public static class UtilZ{
        static double[][] randomCentroids(double[][] data,int k){
            double[][] res = new double[k][];
            for(int i=0;i<k;i++){
                res[i] = data[(int)(Math.random()*data.length)];
            }
            return res;
        }

        static boolean converged(double[][] c1,double[][] c2,double c){
            for(int i=0;i<c1.length;i++){
                if(changed(c1[i],c2[i])>c){
                    return false;
                }
            }
            return true;
        }
        private static double changed(double[] c1,double[] c2){
            double change=0;
            double total=0;
            for(int i=0;i<c1.length;i++){
                total+=Math.pow(c1[i], 2);
                change+=Math.pow(c1[i]-c2[i], 2);
            }
            return Math.sqrt(change/total);
        }

        static double distance(double[] c1,double[] c2){
            double sum = 0;
            for(int i=0;i<c1.length;i++){
                sum+=Math.pow(c1[i]-c2[i], 2);
            }
            return sum;
        }
    }
    public static KMeans build(double[][] input,int k,double c,double[][] cs){
        long start = System.currentTimeMillis();
        MRKDTree tree = MRKDTree.build(input);
        System.out.println("treeConstruct:"+(System.currentTimeMillis()-start));

        double[][] csnew = tree.updateCentroids(cs);
        while(!UtilZ.converged(cs, csnew, c)){
            cs=csnew;
            csnew=tree.updateCentroids(cs);
        }
        KMeans km = new KMeans();
        km.centroids=csnew;
        return km;
    }

    public static KMeans buildOri(double[][] input,int k,double c,double[][] cs){

        double[][] csnew = updateOri(input,cs);
        while(!UtilZ.converged(cs, csnew, c)){
            cs=csnew;
            csnew=updateOri(input,cs);
        }
        KMeans km = new KMeans();
        km.centroids=csnew;
        return km;
    }

    private static double[][] updateOri(double[][] input,double[][] cs){
        int[] center = new int[input.length];
        for(int i=0;i<input.length;i++){
            double dismin = Double.MAX_VALUE;
            for(int j=0;j<cs.length;j++){
                double dis = UtilZ.distance(input[i], cs[j]);
                if(dis<dismin){
                    dismin=dis;
                    center[i]=j;
                }
            }
        }

        double[][] nct =new double[cs.length][cs[0].length];
        int[] datacount = new int[cs.length];
        for(int i=0;i<input.length;i++){
            double[] n = input[i];
            int belong = center[i];
            for(int j=0;j<cs[0].length;j++){
                nct[belong][j]+=n[j];
            }
            datacount[belong]++;
        }

        for(int i=0;i<nct.length;i++){
            for(int j=0;j<nct[0].length;j++){
                nct[i][j]/=datacount[i];
            }
        }
        return nct;
    }

    public void printCentroids(){
        java.text.DecimalFormat df=new java.text.DecimalFormat("0.00");
        for(int i=0;i<centroids.length;i++){
            for(int j=0;j<centroids[i].length;j++)
                System.out.print(df.format(centroids[i][j])+",");
            System.out.println();
        }
    }
}

d.调用

import java.io.BufferedReader;
import java.io.FileReader;

public class Test {
    static void compare(double[][] input){
        double[][] cs = KMeans.UtilZ.randomCentroids(input, 20);
        int t=1;
        long start = System.currentTimeMillis();
        while(t-->0)
            KMeans.build(input, 20, 0.001,cs);
        long kdtree = System.currentTimeMillis()-start;
        t=1;
        start = System.currentTimeMillis();
        while(t-->0)
            KMeans.buildOri(input, 20, 0.001,cs);
        long ori = System.currentTimeMillis()-start;

        System.out.println("kdtree:"+kdtree);
        System.out.println("linear:"+ori);
        System.out.println(ori*1.0/kdtree);
    }

    public static void main(String[] args) throws Exception{
        BufferedReader reader = new BufferedReader(new FileReader("d.txt"));
        String line=null;
        double[][] input = new double[600000][10];
        int i=0;
        while((line=reader.readLine())!=null){
            String[] numstrs=line.split("\t");
            for(int j=0;j<10;j++)
                input[i][j] = Double.parseDouble(numstrs[j]);
            i++;
        }

        compare(input);
    }
}

5.总结

对于数据量较小、中心点较少、维度不多的情景中，使用kd-tree并不能加速，反而比原始的算法更慢，因为kd-tree的构建花费了很长时间；

此时在选择分割维度的时候不用方差，而用数据范围，能加快kd-tree 的构建，但会下降一定的kd-tree查询性能；

当数据量大，中心点多，维度大的情况下或者在x-mean算法中，应该使用方差作为选择分割维度，此时查询性能的提升能弥补kd-tee构建的耗时