C#使用cplex求解简单线性规划问题（Cplex系列-教程二）

若还未在项目中添加cplex的引用，可以参阅上一篇文章。本文主要介绍利用C#求解线性规划的步骤，对线性规划模型进行数据填充的两种方法，以及一些cplex函数的功能和用法。包括以下几个步骤：

描述

先花时间理清问题。明确决策变量及其取值范围，目标函数，约束条件，已知的数据。后面代码的编写也是沿着这个思路，先理清问题后面的工作会更有效率。以如下问题为例：

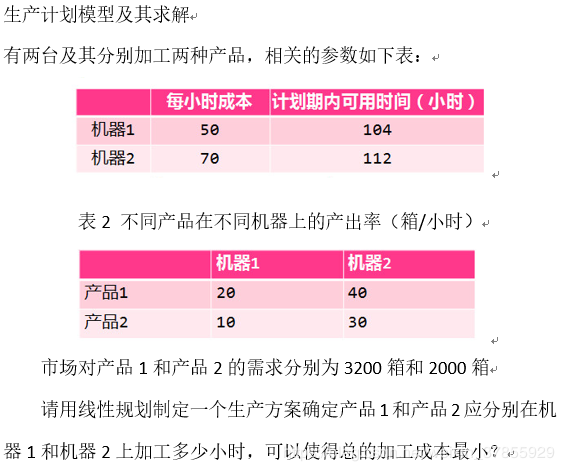
先建立数学模型：
令：i产品在j机器上加工的小时数为xij
决策变量：x11,x12,x21,x22
目标函数：Min(z)=50x11+70x12+50x21+70x22
约束条件：
x₁₂+x₂₂<=112,
x₁₁+x₂₁<=104,
20x₁₁+40x₁₂=3200,
10x21+30x22=2000,
x_ij>=0(i=1,2;j=1,2)

模型

创建模型对象

//实例化一个空模型
Cplex cplexModel = new Cplex();

方法1：使用行方法填充模型

//生成决策变量并约束范围

 INumVar[][] deVar=new INumVar[1][];//交叉数组用于存储决策变量
 double[]lb= {0.0, 0.0, 0.0,0.0}; //lb(low bound)与ub定义决策变量的上下界
 double[]ub={double.MaxValue,double.MaxValue,double.MaxValue,double.MaxValue};
 string []deVarName={"x11","x12","x21","x22"};//决策变量名
 INumVar[]x=cplexModel.NumVarArray(4,lb,ub,deVarName);//生成决策变量
 deVar[0]=x;

//生成目标函数

 double[]objCoef={50.0,70.0,50.0,70.0};//目标函数系数(object coefficient)
 cplexModel.AddMinimize(cplexModel.ScalProd(x, objCoef));//数量相乘（scalar product）

//生成约束条件
IRange[][] rng = new IRange[1][];//存放约束
rng[0] = new IRange[4];
//AddLe为<=，AddGe为>=,AddEq为=
rng[0][0] = cplexModel.AddLe(
cplexModel.Sum(cplexModel.Prod(1.0, x[3]),
               cplexModel.Prod( 1.0, x[1])), 112.0, "c1");
rng[0][1] = cplexModel.AddLe(
cplexModel.Sum(cplexModel.Prod(1.0, x[0]),
               cplexModel.Prod( 1.0, x[2])), 104.0, "c2");
rng[0][2] = cplexModel.AddEq(
cplexModel.Sum(cplexModel.Prod(20.0, x[0]),
               cplexModel.Prod( 40.0, x[1])), 3200.0, "c3");
rng[0][3] = cplexModel.AddEq(
cplexModel.Sum(cplexModel.Prod(10.0, x[2]),
               cplexModel.Prod( 30.0, x[3])), 2000.0, "c4");

方法2：使用列方法填充模型　　

 IObjective obj =cplexModel.AddMinimize();//目标函数，此时是空的
 //约束
 IRange[][] rng=new IRange[1][];
 rng[0]=new IRange[4];
 rng[0][0] = cplexModel.AddRange(-double.MaxValue, 112.0, "c1");//<=112
 rng[0][1] = cplexModel.AddRange(-double.MaxValue, 104.0, "c2");
 rng[0][2] = cplexModel.AddRange(3200.0,3200.0, "c3");//=3200
 rng[0][3] = cplexModel.AddRange(2000.0,2000.0, "c4");
 //简化引用的书写
 IRange r0 = rng[0][0];
 IRange r1 = rng[0][1];
 IRange r2 = rng[0][2];
 IRange r3 = rng[0][3];
 //决策变量
 INumVar[][]deVar=new INumVar[1][];
 deVar[0]=new INumVar[4];//4个决策变量
 deVar[0][0] = cplexModel.NumVar(cplexModel.Column(obj, 50.0).And(
                               cplexModel.Column(r1,  1.0).And(
                               cplexModel.Column(r2,   20.0))),
                               0.0, double.MaxValue, "x11");//最后一行为取值和名称
deVar[0][1] = cplexModel.NumVar(cplexModel.Column(obj, 70.0).And(
                               cplexModel.Column(r0,  1.0).And(
                               cplexModel.Column(r2,   40.0))),
                               0.0, double.MaxValue, "x12");
deVar[0][2] = cplexModel.NumVar(cplexModel.Column(obj, 50.0).And(
                               cplexModel.Column(r1,  1.0).And(
                               cplexModel.Column(r3,   10.0))),
                               0.0, double.MaxValue, "x21");
deVar[0][3] = cplexModel.NumVar(cplexModel.Column(obj, 70.0).And(
                               cplexModel.Column(r0,  1.0).And(
                               cplexModel.Column(r3,   30.0))),
                               0.0, double.MaxValue, "x22");

求解模型并展示　　

if (cplexModel.Solve())
            {
                int nvars = cplexModel.GetValues(deVar[0]).Length;
                for (int j = 0; j < nvars; ++j)
                {
                    cplexModel.Output().WriteLine("Variable   " + j +": Value = " + cplexModel.GetValues(deVar[0])[j] );
                }
            }

导出模型　　

cplexModel.ExportModel("lpex1.lp");

文件在“你的项目\bin\debug”显示如下图：

　　

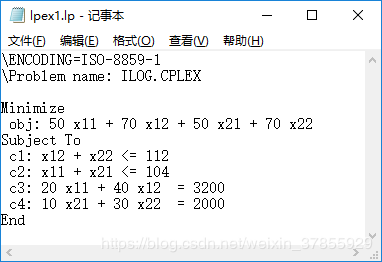
完整代码和求解结果

using ILOG.Concert;
using ILOG.CPLEX;
using System;

public class LPex1
{
    public static void Main(string[] args)
    {
        try
        {
            //实例化一个空模型
            Cplex cplexModel = new Cplex();
            //生成决策变量并赋值
            INumVar[][] deVar = new INumVar[1][];
            double[] lb = { 0.0, 0.0, 0.0, 0.0 };
            double[] ub = { double.MaxValue, double.MaxValue, double.MaxValue, double.MaxValue };
            string[] deVarName = { "x11", "x12", "x21", "x22" };
            INumVar[] x = cplexModel.NumVarArray(4, lb, ub, deVarName);
            deVar[0] = x;
            //目标函数
            double[] objCoef = { 50.0, 70.0, 50.0, 70.0 };//目标函数系数(object coefficient)
            cplexModel.AddMinimize(cplexModel.ScalProd(x, objCoef));
            //约束条件
            IRange[][] rng = new IRange[1][];
            rng[0] = new IRange[4];
            rng[0][0] = cplexModel.AddLe(cplexModel.Sum(cplexModel.Prod(1.0, x[3]),
                                                       cplexModel.Prod(1.0, x[1])), 112, "c1");
            rng[0][1] = cplexModel.AddLe(cplexModel.Sum(cplexModel.Prod(1.0, x[0]),
                                                         cplexModel.Prod(1.0, x[2])), 104.0, "c2");
            rng[0][2] = cplexModel.AddEq(cplexModel.Sum(cplexModel.Prod(20.0, x[0]),
                                                         cplexModel.Prod(40.0, x[1])), 3200.0, "c3");
            rng[0][3] = cplexModel.AddEq(cplexModel.Sum(cplexModel.Prod(10.0, x[2]),
                                                        cplexModel.Prod(30.0, x[3])), 2000.0, "c4");
            cplexModel.ExportModel("lpex1.lp");

            if (cplexModel.Solve())
            {
                int nvars = cplexModel.GetValues(deVar[0]).Length;
                for (int j = 0; j < nvars; ++j)
                {
                    cplexModel.Output().WriteLine("Variable   " + j +": Value = " + cplexModel.GetValues(deVar[0])[j] );
                }
            }
            cplexModel.End();
        }
        catch (ILOG.Concert.Exception e)
        {
            System.Console.WriteLine("Concert exception '" + e + "' caught");
        }
        Console.ReadKey();
    }
}

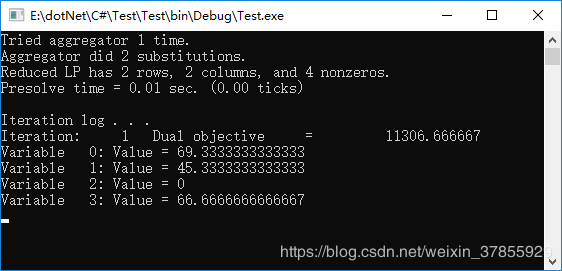
决策变量较多时，请使用循环。本文重在入门和对cplex库中一些概念的理解。