EOJ Monthly 2019.2 (based on February Selection) F.方差

题目链接：

　　https://acm.ecnu.edu.cn/contest/140/problem/F/

题目：

思路：

　　

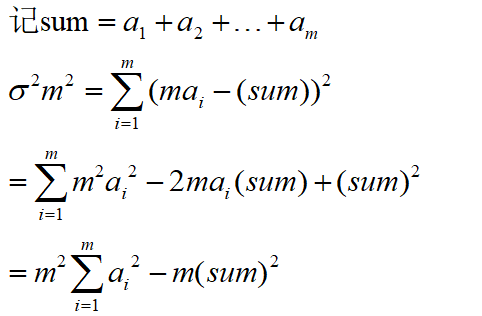
　　因为方差是用来评估数据的离散程度的，因此最优的m个数一定是排序后连续的，所以我们可以先排序然后对每m个连续的数取个min。

代码实现如下：

 #include <set>
 #include <map>
 #include <deque>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <ctime>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pLL;
 typedef pair<LL, int> pLi;
 typedef pair<int, LL> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson rt<<1
 #define rson rt<<1|1
 #define lowbit(x) x&(-x)
 #define name2str(name) (#name)
 #define bug printf("*********\n")
 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
 #define FIN freopen("D://code//in.txt","r",stdin)
 #define IO ios::sync_with_stdio(false),cin.tie(0)

 const double eps = 1e-;
 const int mod = ;
 const int maxn = 1e6 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const LL INF = 0x3f3f3f3f3f3f3f3fLL;

 int n, m;
 int a[maxn];
 LL sum1[maxn], sum2[maxn];

 int main(){
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; i++) {
         scanf("%d", &a[i]);
     }
     sort(a + , a + n + );
     for(int i = ; i <= n; i++) {
         sum1[i] = sum1[i-] + a[i];
         sum2[i] = sum2[i-] + a[i] * a[i];
     }
     LL ans = INF;
     for(int i = ; i <= n - m + ; i++) {
         ans = min(ans, m * (sum2[i+m-] - sum2[i-]) - (sum1[i+m-] - sum1[i-]) * (sum1[i+m-] - sum1[i-]));
     }
     printf("%lld\n", ans);
     return ;
 }