c语言数字图像处理(十):阈值处理
定义
全局阈值处理
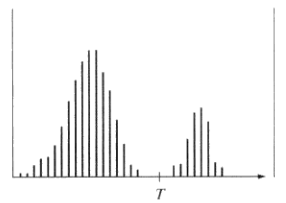
假设某一副灰度图有如下的直方图,该图像由暗色背景下的较亮物体组成,从背景中提取这一物体时,将阈值T作为分割点,分割后的图像g(x, y)由下述公式给出,称为全局阈值处理
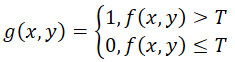
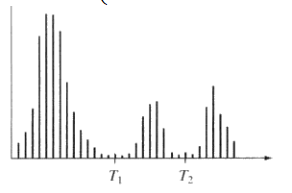
多阈值处理
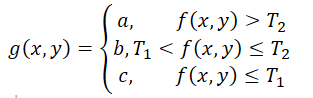
本文仅完成全局阈值处理的算法实现
基本全局阈值处理方法
1. 为全局阈值T选择一个初始的估计值
2. 用T分割图像,产生两组像素:G1由大于T的像素组成,G2由小于T的像素组成
3. 对G1和G2的像素分别计算平均灰度值m1和m2
4. 计算新的阈值T = 1/2 * (m1 + m2)
5. 重复步骤2-4,直到连续迭代中的T值差小于一个预定义的参数ΔT
算法实现
void threshold(short** in_array, short** out_array, long height, long width, int delt_t)
{
double T = 0xff / 2.0;
double m1 = 0.0, m2 = 0.0;
int m1_num = , m2_num = ; while(dabs(T, 0.5*(m1 + m2)) > delt_t){
T = 0.5 * (m1 + m2);
m1 = 0.0;
m2 = 0.0;
m1_num = ;
m2_num = ; for (int i = ; i < height; i++){
for (int j = ; j < width; j++){
if (in_array[i][j] <= T){
m1 += in_array[i][j];
m1_num++;
}
else{
m2 += in_array[i][j];
m2_num++;
}
}
}
if (m1_num != )
m1 /= m1_num;
if (m2_num != )
m2 /= m2_num;
printf("%lf\n", T);
}
for (int i = ; i < height; i++){
for (int j = ; j < width; j++){
if (in_array[i][j] <= T)
out_array[i][j] = 0xff;
else
out_array[i][j] = 0x00;
}
}
}
测试结果

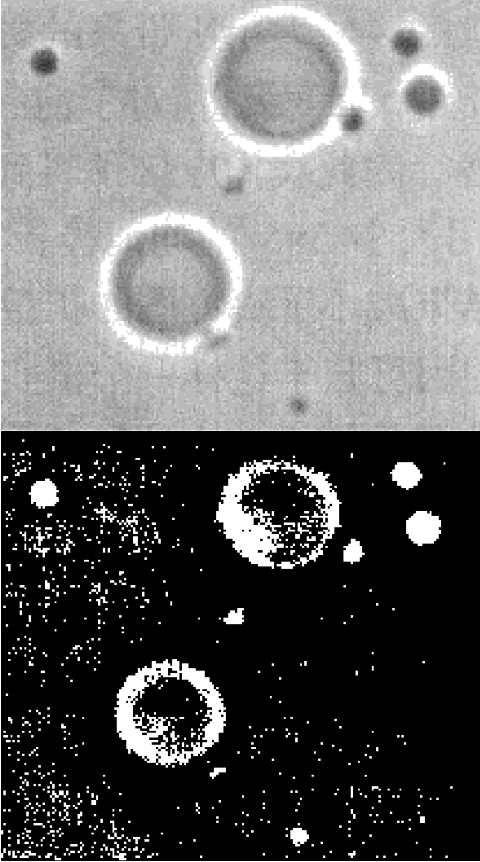
从实验结果看出,第二组阈值处理的效果并不好,因此考虑更优的算法实现
Otsu方法进行最佳全局阈值处理
阈值处理可视为一种统计决策理论问题,其目的是在把像素分配给两个或多个组的过程中引入的平均误差最小。这一问题有个闭合形式的解,称为贝叶斯决策规则。
Otsu方法在类间方差最大的情况下是最佳的
算法执行流程

代码实现
double dabs(double a, double b)
{
if (a < b)
return b-a;
else
return a-b;
} void calculate_histogram(long height, long width, short **image, unsigned long histogram[])
{
short k;
for(int i=; i < height; i++){
for(int j=; j < width; j++){
k = image[i][j];
histogram[k] = histogram[k] + ;
}
}
} void calculate_pi(long height, long width, unsigned long histogram[], double pi[])
{
for (int i = ; i < GRAY_LEVELS; ++i){
pi[i] = (double)histogram[i] / (double)(height * width);
}
} double p1(int k, double pi[])
{
double sum = 0.0; for (int i = ; i <= k; i++){
sum += pi[i];
} return sum;
} double m(int k, double pi[])
{
double sum = 0.0; for (int i = ; i <= k; i++){
sum += i * pi[i];
} return sum;
} double calculate_sigma(int k, double mg, double pi[])
{
double p1k = p1(k, pi);
double mk = m(k, pi); if (p1k < 1e- || ( - p1k) < 1e-)
return 0.0;
else
return pow(mg * p1k - mk, ) / (p1k * ( - p1k));
} void otsu(short** in_array, short** out_array, long height, long width)
{
unsigned long histogram[GRAY_LEVELS] = {};
double pi[GRAY_LEVELS] = {};
double sigma[GRAY_LEVELS] = {};
double mg;
short max_count = ;
short k = ;
double max_value = 0.0;
double k_star; calculate_histogram(height, width, in_array, histogram);
calculate_pi(height, width, histogram, pi);
mg = m(GRAY_LEVELS-, pi); for (int i = ; i < GRAY_LEVELS; i++)
sigma[i] = calculate_sigma(i, mg, pi); max_value = sigma[];
max_count = ;
k = ;
for (int i = ; i < GRAY_LEVELS; i++){
if (dabs(sigma[i], max_value) < 1e-){
k += i;
max_count++;
}
else if (sigma[i] > max_value){
max_value = sigma[i];
max_count = ;
k = i;
}
}
k_star = k / max_count; printf("%lf\n", k_star);
for (int i = ; i < height; i++){
for (int j = ; j < width; j++){
if (in_array[i][j] <= k_star)
out_array[i][j] = 0x00;
else
out_array[i][j] = 0xff;
}
}
}
结果
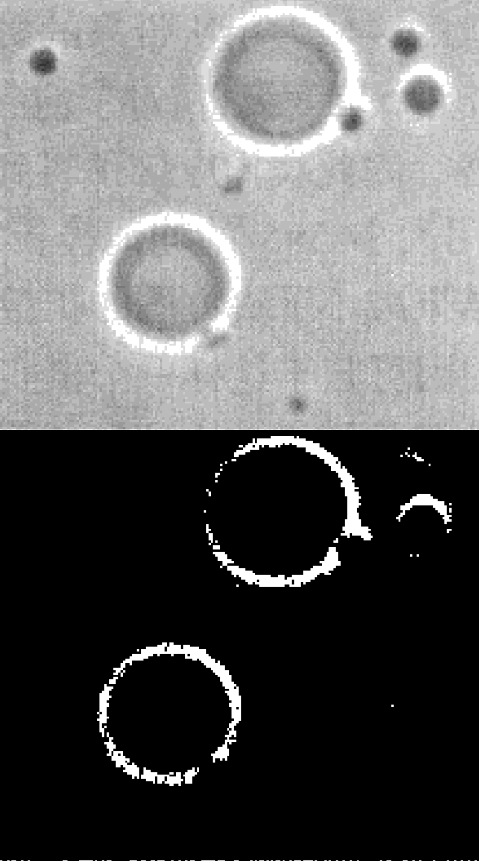
c语言数字图像处理(十):阈值处理的更多相关文章
- c语言数字图像处理(三):仿射变换
仿射变换及坐标变换公式 几何变换改进图像中像素间的空间关系.这些变换通常称为橡皮模变换,因为它们可看成是在一块橡皮模上印刷一幅图像,然后根据预定的一组规则拉伸该薄膜.在数字图像处理中,几何变换由两个基 ...
- c语言数字图像处理(九):边缘检测
背景知识 边缘像素是图像中灰度突变的像素,而边缘是连接边缘像素的集合.边缘检测是设计用来检测边缘像素的局部图像处理方法. 孤立点检测 使用<https://www.cnblogs.com/Gol ...
- c语言数字图像处理(五):空间滤波
空间滤波原理 使用大小为m*n的滤波器对大小为M*N的图像进行线性空间滤波,将滤波器模板乘以图像中对应灰度值,相加得模板中心灰度值 a = (m-1)/2, b = (n-1)/2 若f(x+s, y ...
- c语言数字图像处理(二):图片放大与缩小-双线性内插法
图像内插 假设一幅大小为500 * 500的图像扩大1.5倍到750 * 750,创建一个750 * 750 的网格,使其与原图像间隔相同,然后缩小至原图大小,在原图中寻找最接近的像素(或周围的像素) ...
- c语言数字图像处理(一):bmp图片格式及灰度图片转换
本篇文章首先介绍了bmp图片格式,主要参考wiki上的内容,包括bmp文件的存储方式,对于一些常见的bmp文件格式都给了例子,并且对8位 16位RGB555 16位RGB565格式的bmp文件进行了简 ...
- c语言数字图像处理(八):噪声模型及均值滤波器
图像退化/复原过程模型 高斯噪声 PDF(概率密度函数) 生成高斯随机数序列 算法可参考<http://www.doc.ic.ac.uk/~wl/papers/07/csur07dt.pdf&g ...
- c语言数字图像处理(七):频率域滤波
代码运行了两个小时才出的结果,懒得测试了,这一部分先鸽了,等对DFT算法进行优化后再更
- c语言数字图像处理(六):二维离散傅里叶变换
基础知识 复数表示 C = R + jI 极坐标:C = |C|(cosθ + jsinθ) 欧拉公式:C = |C|ejθ 有关更多的时域与复频域的知识可以学习复变函数与积分变换,本篇文章只给出DF ...
- c语言数字图像处理(四):灰度变换
灰度变换 灰度变换函数 s = T(r) 其中r为输入图像在(x, y)点处的灰度值,s为输出图像在(x, y)点处的灰度值 灰度变换的作用 上图所示的两幅T(s)函数的图像曲线,第一幅图可以增强 ...
随机推荐
- 在web.xml中配置404错误拦截
<error-page> <error-code>404</error-code> <location>/home.do</location> ...
- 【原创】python内存泄漏以及python flask框架莫名coredump
1.python内存泄漏 今天在看服务器上的进程时,用top查的时候,发现一个一直跑的脚本程序内存竟然达到了1.6G,这个脚本我有印象,一开始仅占用20M左右,显然是内存泄漏了. 用gc和objgra ...
- UVa 1363 - Joseph's Problem(数论)
链接: https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem& ...
- 【bzoj 3252】攻略
题意 我们想到一个贪心,就是每次找到根路径前缀和最大的一个点,取走这条路径,同时把这条路径上的点权变成\(0\) 正确性显然 进一步发现我们需要从树上选择\(m\)条链使得链的总和最大 于是我们考虑换 ...
- 20145203盖泽双 《Java程序设计》第十周学习总结
20145203盖泽双 <Java程序设计>第十周学习总结 教材学习内容总结 一.网络概述 1.网络编程就是两个或多个设备(程序)之间的数据交换. 2.识别网络上的每个设备:①IP地址②域 ...
- Oracle 表单的创建
1.-- 连接 conn hu/aaa; -- 创建表空间 Create tablespace computer2005 nologging datafile 'd:/Oracle/product/1 ...
- SEGGER RTT STOP/SLEEP 模式下使用
1.问题详述, M3/M4内核在sleep 或者 STOP模式 下,内核是不工作的,因此需要 以下 几步操作 第一步: 开启 低功耗模式下,debug 的连接 DBGMCU_Config(DBGMCU ...
- iOS如何在一个包上切换正式环境和测试环境
最近项目处于测试阶段,所以免不了每天都得打包给测试人员,由于我们公司规模比较大,项目环境也分为了三种:测试环境.预上线(预生产)环境.上线(生产)环境.所以每到了测试后期,每天打包的时间也占了不少,遇 ...
- 【js】走近小程序
一.什么是小程序? 基于微信的可以为用户提供一些服务的web项目,利用微信提供的接口可以让所有开发者使用到微信的原生能力,去完成一些之前做不到或者难以做到的事情. 二.小程序开发工具以及语言? 小程序 ...
- Tarjan算法初探 (1):Tarjan如何求有向图的强连通分量
在此大概讲一下初学Tarjan算法的领悟( QwQ) Tarjan算法 是图论的非常经典的算法 可以用来寻找有向图中的强连通分量 与此同时也可以通过寻找图中的强连通分量来进行缩点 首先给出强连通分量的 ...
