浅谈kmp

简介:

一种由Knuth(D.E.Knuth)、Morris(J.H.Morris）和Pratt(V.R.Pratt）三人设计的线性时间字符串匹配算法。这个算法不用计算变迁函数δ，匹配时间为Θ（n），只用到辅助函数π[1，m]，它是在Θ（m）时间内，根据模式预先计算出来的。数组π使得我们可以按需要，“现场”有效的计算（在平摊意义上来说）变迁函数δ。粗略地说，对任意状态q=0，1，…，m和任意字符a∈Σ，π[q]的值包含了与a无关但在计算δ（q，a）时需要的信息。由于数组π只有m个元素，而δ有Θ（m∣Σ∣）个值，所以通过预先计算π而不是δ，使得时间减少了一个Σ因子

以上摘自百度百科。。。

简单的来说，kmp就是一种高效的字符串匹配算法，它能够快速的处理出模式串与文本串的匹配

步骤:

预处理出nxt数组

首先，我们要明确数组的概念，我们定义nxt数组为最长真前后缀

即 \(nxt[i]=\{max(j)|s[1\,to\,j]=s[i-j+1\,to\,i]\}\)

这有什么用呢？

在传统的O(n^2)字符串匹配算法里，我们每次匹配失败时，就要重新跳到初始点匹配，然而事实上我们是不需要去这样匹配的

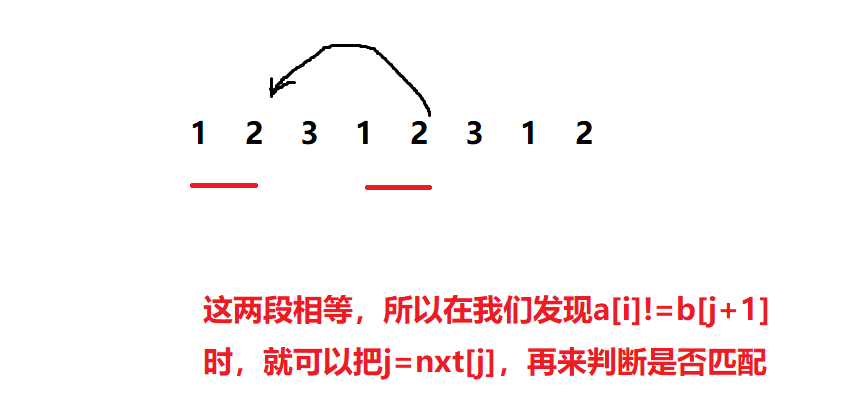
假设我们已经匹配到了模式串b的第j个字符，文本串a的第i-1个字符，发现\(b[j+1]\ne a[i]\)，但我们可以知道\(b[1\,to\,j]=a[i-j\,to\,i-1]\)，这个条件显然是可以利用的。

假如前面有一段，和我们匹配完的这一段是相等的，那么我们显然不需要再到\(b[1]\)去逐字匹配，我们可以直接跳到那一段的末尾，再来跟\(a[i]\)匹配，看是否相等

\(nxt\)数组就是来提供每次失配后跳的位置的，我们来看一下\(nxt\)数组

1 2 3 1 2 3 2

0 0 0 1 2 3 0

上面是模式串，下面是\(nxt\)数组，可以看图理解一下,以\(b[5]\)为例

那么，如何去得出\(nxt\)数组呢？

显然，是不能用暴力枚举的，否则时间复杂度还是O(n^2)，就与我们的初衷相悖，所以我们要找到一种快速的处理出nxt数组的方式

假设我们已经求出了\(nxt[1\,to\,i-1]\)，现在我们要求\(nxt[i]\)，怎么快速的得到它的\(nxt\)值呢？

设\(j=nxt[i-1]\)，即\(b[1\,to\,j]=b[i-j\,to\,j]\)，那么只要\(b[j+1]=b[i]\)，显然就可以得知\(nxt[i]=j+1\)，否则，我们就令\(j=nxt[j]\)，再来判断(因为这时nxt[j]~j之间的值都肯定不是，没理解的话可以自己画图理解)

代码实现：

void getnxt(){
    nxt[1]=0;//数组下标从1开始,nxt[1]显然等于0
    for(int i=2,j=0;i<=len;i++){
        while(j>0&&b[i]!=b[j+1])j=nxt[j];
        if(b[i]==b[j+1])j++;
        nxt[i]=j;
    }
}

例题:

Hdu1711 Number Sequence

显然，这道题只需要先把\(nxt\)数组处理出来，匹配的时候，如果匹配到模式串的末尾，就return

Code:

#include<bits/stdc++.h>
using namespace std;
#define N 1000100
int n,m,nxt[N],a[N],b[N];
void getnxt(){
    nxt[1]=0;
    for(int i=2,j=0;i<=m;i++){
        while(j&&b[i]!=b[j+1]) j=nxt[j];
        if(b[i]==b[j+1]) j++;
        nxt[i]=j;
    }
}
int kmp(){
    int i=1,j=0;
    while(i<=n){
        while(j&&a[i]!=b[j+1]) j=nxt[j];
        if(a[i]==b[j+1]) j++;
        if(j==m) return i-m+1;
        i++;
    }
    return -1;
}
int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-f;ch=getchar();}
    while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
    return x*f;
}
int main(){
    int Case=read();
    begin:Case--;
    if(Case<0)return 0;
    n=read();m=read();
    for(int i=1;i<=n;i++)a[i]=read();
    for(int i=1;i<=m;i++)b[i]=read();
    getnxt();printf("%d\n",kmp());
    goto begin;
}