HMM算法

HMM的应用

HMM是生成模型

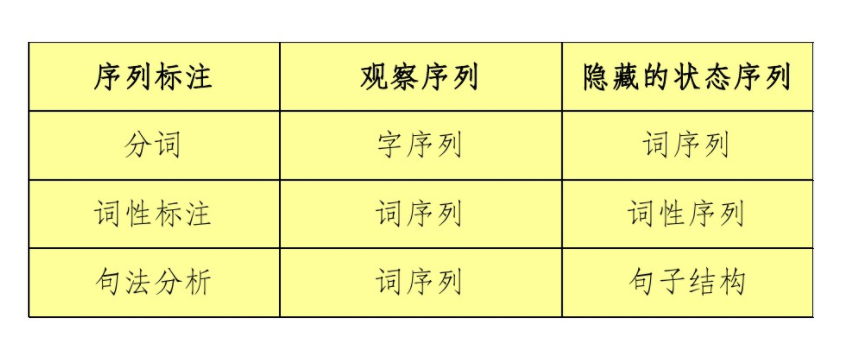
• 词性标注：给定一个词的序列（也就是句子），找出最可能的词性序列（标签是词性）。如ansj分词和ICTCLAS分词等。

• 分词：给定一个字的序列，找出最可能的标签序列（断句符号：[词尾]或[非词尾]构成的序列）。结巴分词目前就是利用BMES标签来分词的，B（开头）,M（中间),E(结尾),S(独立成词）

• 命名实体识别：给定一个词的序列，找出最可能的标签序列（内外符号：[内]表示词属于命名实体，[外]表示不属于）。如ICTCLAS实现的人名识别、翻译人名识别、地名识别都是用同一个Tagger实现的。

HMM的三种问题：

1）知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。

2）还是知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。

3）知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）。