Solution -「LOCAL」大括号树

\(\mathcal{Description}\)

  OurTeam & OurOJ.

  给定一棵 \(n\) 个顶点的树，每个顶点标有字符 ( 或 )。将从 \(u\) 到 \(v\) 的简单有向路径上的字符串成括号序列，记其正则匹配的子串个数为 \(\operatorname{ans}(u,v)\)。求：

\[\sum_{u=1}^n\sum_{v=1}^n\operatorname{ans}(u,v)\bmod998244353
\]

  \(n\le2\times10^5\)。

\(\mathcal{Solution}\)

  可以先回忆一下括号树嗷。

  来看看链怎么做 owo，现有结点按 \(1\sim n\) 从左到右编号，记 \(s(i,j)\) 表示从 \(i\) 到 \(j\) 串成的括号序列。令 \(\operatorname{match}(i)\) 为最大的 \(j<i\)，满足 \(s(j,i)\) 正则匹配。定义状态 \(f(i)\) 表示 \(s(1,i)\) 中，以 \(i\) 结尾的正则子串贡献。那么：

\[f(i)=f(\operatorname{match}(i)-1)+\operatorname{match}(i)
\]

  即，先保证最短的以 \(i\) 结尾的正则，起点就可以在前面任选了。而事实上，终点也能任选，那么答案为：

\[\sum_{i=1}^nf(i)(n-i+1)
\]

  需要正反分别做一次嗷。

---

  那么，搬到树上，一个正则会贡献多少次呢？如图（混V的请告诉我背景是谁吖~）：

  

  不难发现，\((u,v)\)（或 \((v,u)\)）若正则匹配，则它对答案的贡献为 \(siz_u\times siz_v\)。

  好啦，开始 \(\text{DSU on Tree}\) 吧！

  注意到我们只关心一些子树大小的信息，所以这样设计状态：

• \(f(u,i)\) 表示 \(u\) 子树内某一点 \(v\) 到 \(u\)，构成的串有 \(i\) 个 ( 失配，且所有 ) 被匹配的 \(siz_v\) 之和。
• \(g(u,i)\) 表示 \(u\) 到其子树内某一点 \(v\)，构成的串有 \(i\) 个 ) 失配，且所有 ( 被匹配的 \(siz_v\) 之和。

  好奇怪的定义 qwq，该怎样理解呢？

  考虑一条 \(v-u-w\) 的有向树链，其中 \(u\) 是 \(v\) 与 \(w\) 的 \(\text{LCA}\)。若 \(v-u\) 长成 (...((...(，\(u-w\) 长成 ...)...)...))，其中 ... 是已匹配的括号。可见 \(v-u-w\) 是正则匹配的，而这正对应了我们的状态 \(f(u,4)\) 和 \(g(u,4)\)！

  接着考虑轻重儿子信息对答案的贡献，如图：

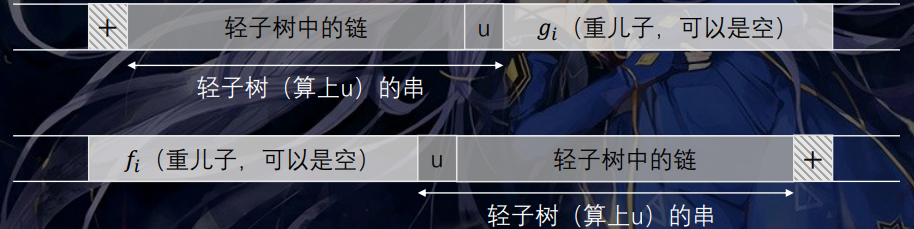
  \(\text{DFS}\) 轻儿子的时候，用线段树动态维护前缀的 )，后缀的 ( 是否出现失配的情况，若一个点加入后不存在失配，则用 DP 信息更新答案。合并信息时类似，但加入最后一个点 \(u\) 时：

• \(s_u=\texttt{'('}\)，\(f(u,i+1)=f(v,i)\)，\(g(u,i-1)=f(v,i)\)。

• \(s_u=\texttt{')'}\)，\(f(u,i-1)=f(v,i)\)，\(g(u,i+1)=f(v,i)\)。

  这……总不可能 \(\mathcal O(siz)\) 地遍历第二维吧 qwq。事实上，发现这只是一个单纯的数组位移，初始时开两倍数组，用一个指针指向数组实际的 \(0\) 号为即可 \(\mathcal O(1)\) 实现了。

  以上两幅配图来自 Lucky_Glass 的题解。

\(\mathcal{Code}\)

#include <cstdio>

const int MAXN = 2e5, MOD = 998244353;
int n, ecnt, head[MAXN + 5], siz[MAXN + 5], son[MAXN + 5];
int ans, aryf[MAXN * 2 + 5], aryg[MAXN * 2 + 5], *f, *g;
char s[MAXN + 5];

inline int add ( int a, const int b ) { return ( a += b ) < MOD ? a : a - MOD; }
inline int sub ( int a, const int b ) { return ( a -= b ) < 0 ? a + MOD : a; }
inline int mul ( long long a, const int b ) { return ( a *= b ) < MOD ? a : a % MOD; }

inline int rint () {
	int x = 0; char s = getchar ();
	for ( ; s < '0' || '9' < s; s = getchar () );
	for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
	return x;
}

struct Edge { int to, nxt; } graph[MAXN + 5];

inline void link ( const int s, const int t ) {
	graph[++ ecnt] = { t, head[s] };
	head[s] = ecnt;
}

struct SegmentTree {
	int mn[MAXN * 2 + 5], tag[MAXN * 2 + 5];

	inline int id ( const int l, const int r ) { return ( l + r ) | ( l != r ); }
	inline void pushad ( const int l, const int r, const int v ) {
		int rt = id ( l, r );
		mn[rt] += v, tag[rt] += v;
	}
	inline void pushdn ( const int l, const int r ) {
		int rt = id ( l, r ), mid = l + r >> 1;
		if ( ! tag[rt] ) return ;
		pushad ( l, mid, tag[rt] ), pushad ( mid + 1, r, tag[rt] );
		tag[rt] = 0;
	}
	inline void pushup ( const int l, const int r ) {
		int rt = id ( l, r ), mid = l + r >> 1, lc = id ( l, mid ), rc = id ( mid + 1, r );
		mn[rt] = mn[lc] < mn[rc] ? mn[lc] : mn[rc];
	}
	inline void update ( const int l, const int r, const int ul, const int ur, const int v ) {
		if ( ul <= l && r <= ur ) return pushad ( l, r, v );
		int mid = l + r >> 1; pushdn ( l, r );
		if ( ul <= mid ) update ( l, mid, ul, ur, v );
		if ( mid < ur ) update ( mid + 1, r, ul, ur, v );
		pushup ( l, r );
	}
	inline bool check () { return mn[id ( 1, n )] >= 0; }
} preT, sufT; // ((... and ...)), preT->g, sufT->f.

inline void init ( const int u ) {
	siz[u] = 1;
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		init ( v = graph[i].to ), siz[u] += siz[v];
		if ( siz[son[u]] < siz[v] ) son[u] = v;
	}
}

inline void update ( const int u, const int dep, const int k ) {
	preT.update ( 1, n, 1, dep, s[u] == '(' ? k : -k );
	sufT.update ( 1, n, 1, dep, s[u] == ')' ? k : -k );
}

inline void calc ( const int u, int cnt, const int dep ) {
	cnt += s[u] == ')' ? 1 : -1, update ( u, dep, 1 );
	if ( sufT.check () ) ans = add ( ans, mul ( siz[u], f[cnt] ) );
	if ( preT.check () ) ans = add ( ans, mul ( siz[u], g[-cnt] ) );
	for ( int i = head[u]; i; i = graph[i].nxt ) calc ( graph[i].to, cnt, dep + 1 );
	update ( u, dep, -1 );
}

inline void coll ( const int u, int cnt, const int dep ) {
	cnt += s[u] == '(' ? 1 : -1, update ( u, dep, -1 );
	if ( sufT.check () ) f[cnt] = add ( f[cnt], siz[u] );
	if ( preT.check () ) g[-cnt] = add ( g[-cnt], siz[u] );
	for ( int i = head[u]; i; i = graph[i].nxt ) coll ( graph[i].to, cnt, dep + 1 );
	update ( u, dep, 1 );
}

inline void solve ( const int u, const bool keep ) {
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( ( v = graph[i].to ) ^ son[u] ) {
			solve ( v, false );
		}
	}
	if ( son[u] ) solve ( son[u], true );
	if ( s[u] == '(' ) ans = add ( ans, mul ( g[1], n - siz[son[u]] ) );
	if ( s[u] == ')' ) ans = add ( ans, mul ( f[1], n - siz[son[u]] ) );
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( ( v = graph[i].to ) ^ son[u] ) {
			*f = add ( *f, n - siz[v] ), g[0] = add ( *g, n - siz[v] );
			update ( u, 1, 1 );
			calc ( v, s[u] == ')' ? 1 : -1, 2 );
			*f = sub ( *f, n - siz[v] ), g[0] = sub ( *g, n - siz[v] );
			update ( u, 1, -1 );
			coll ( v, 0, 1 );
		}
	}
	if ( s[u] == '(' ) *f = add ( *f, siz[u] ), -- f, *g ++ = 0;
	if ( s[u] == ')' ) *g = add ( *g, siz[u] ), -- g, *f ++ = 0;
	if ( ! keep ) {
		for ( int i = 0; i <= siz[u]; ++ i ) f[i] = g[i] = 0;
		f = aryf + n, g = aryg + n;
	}
}

int main () {
	scanf ( "%d %s", &n, s + 1 );
	for ( int i = 2; i <= n; ++ i ) link ( rint (), i );
	init ( 1 );
	f = aryf + n, g = aryg + n;
	solve ( 1, true );
	printf ( "%d\n", ans );
	return 0;
}

\(\mathcal{Update}\)

  然后你就发现……只需要维护前缀、后缀最大值，与当前前缀、后缀和比较就砍掉 \(\log\) 了 owo！

#include <cstdio>

const int MAXN = 2e5, MOD = 998244353;
int n, ecnt, head[MAXN + 5], siz[MAXN + 5], son[MAXN + 5];
int ans, aryf[MAXN * 2 + 5], aryg[MAXN * 2 + 5], *f, *g;
char s[MAXN + 5];

inline int add ( int a, const int b ) { return ( a += b ) < MOD ? a : a - MOD; }
inline int sub ( int a, const int b ) { return ( a -= b ) < 0 ? a + MOD : a; }
inline int mul ( long long a, const int b ) { return ( a *= b ) < MOD ? a : a % MOD; }
inline void chkmax ( int& a, const int b ) { if ( a < b ) a = b; }

inline int rint () {
	int x = 0; char s = getchar ();
	for ( ; s < '0' || '9' < s; s = getchar () );
	for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
	return x;
}

struct Edge { int to, nxt; } graph[MAXN + 5];

inline void link ( const int s, const int t ) {
	graph[++ ecnt] = { t, head[s] };
	head[s] = ecnt;
}

inline void init ( const int u ) {
	siz[u] = 1;
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		init ( v = graph[i].to ), siz[u] += siz[v];
		if ( siz[son[u]] < siz[v] ) son[u] = v;
	}
}

inline void calc ( const int u, int cnt, int pre, int suf ) {
	cnt += s[u] == ')' ? 1 : -1;
	chkmax ( pre, -cnt ), chkmax ( suf, cnt );
	if ( suf == cnt ) ans = add ( ans, mul ( siz[u], f[cnt] ) );
	if ( pre == -cnt ) ans = add ( ans, mul ( siz[u], g[-cnt] ) );
	for ( int i = head[u]; i; i = graph[i].nxt ) calc ( graph[i].to, cnt, pre, suf );
}

inline void coll ( const int u, int cnt, int pre, int suf ) {
	cnt += s[u] == '(' ? 1 : -1;
	chkmax ( pre, -cnt ), chkmax ( suf, cnt );
	if ( suf == cnt ) f[cnt] = add ( f[cnt], siz[u] );
	if ( pre == -cnt ) g[-cnt] = add ( g[-cnt], siz[u] );
	for ( int i = head[u]; i; i = graph[i].nxt ) coll ( graph[i].to, cnt, pre, suf );
}

inline void solve ( const int u, const bool keep ) {
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( ( v = graph[i].to ) ^ son[u] ) {
			solve ( v, false );
		}
	}
	if ( son[u] ) solve ( son[u], true );
	if ( s[u] == '(' ) ans = add ( ans, mul ( g[1], n - siz[son[u]] ) );
	if ( s[u] == ')' ) ans = add ( ans, mul ( f[1], n - siz[son[u]] ) );
	int pre = s[u] == '(' ? 1 : -1, suf = s[u] == ')' ? 1 : -1;
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( ( v = graph[i].to ) ^ son[u] ) {
			*f = add ( *f, n - siz[v] ), g[0] = add ( *g, n - siz[v] );
			calc ( v, s[u] == ')' ? 1 : -1, pre, suf );
			*f = sub ( *f, n - siz[v] ), g[0] = sub ( *g, n - siz[v] );
			coll ( v, 0, 0, 0 );
		}
	}
	if ( s[u] == '(' ) *f = add ( *f, siz[u] ), -- f, *g ++ = 0;
	if ( s[u] == ')' ) *g = add ( *g, siz[u] ), -- g, *f ++ = 0;
	if ( ! keep ) {
		for ( int i = 0; i <= siz[u]; ++ i ) f[i] = g[i] = 0;
		f = aryf + n, g = aryg + n;
	}
}

int main () {
	scanf ( "%d %s", &n, s + 1 );
	for ( int i = 2; i <= n; ++ i ) link ( rint (), i );
	init ( 1 );
	f = aryf + n, g = aryg + n;
	solve ( 1, true );
	printf ( "%d\n", ans );
	return 0;
}