（精）题解 guP2860 [USACO06JAN]冗余路径Redundant Paths

（写题解不容易，来我的博客玩玩咯qwq~）

该题考察的知识点是边双连通分量

边双连通分量即一个无向图中，去掉一条边后仍互相连通的极大子图。（单独的一个点也可能是一个边双连通分量）

换言之，一个边双连通分量中不包含桥。

例如下图（样例）中的边双连通分量有(1)，(2,3,5,6)，(4)，(7)

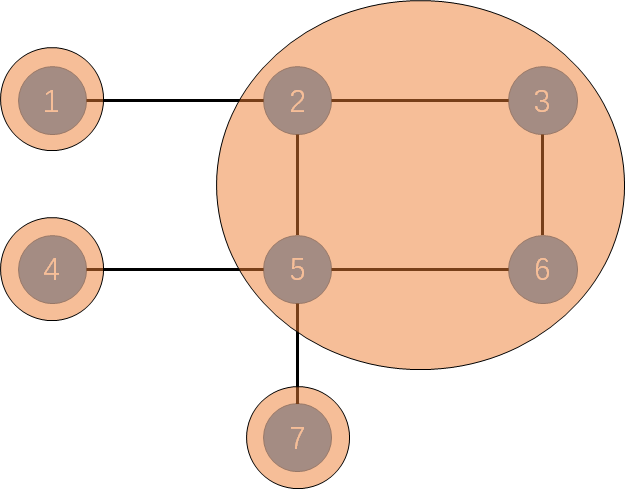
不难发现，在一个边双连通分量中，任意两点都存在至少两条互相分离的路径；（如1->2与1->3->2）

如若不在一个边双连通分量中，则可能经过桥（甚至不联通）如：2->4。

由于桥是必须通过的，所以不存在两条互相分离的路径（或没有路径）。我们要做的，就是连边将整张图变成一张边双连通图。

（正文好像才开始）

首先是找出所有边双连通分量。不难发现，边双连通分量不包含桥，因此我们只需将桥无视掉，每一个连通的子图就是一个边双连通分量。（桥的公式大家都知道吧）代码如下：

void tarjan(int u,int edge)
{
    dfn[u]=low[u]=++num;
    for(int i=fst[u];i!=0;i=nex[i])
    {
        int v=to[i];
        if(!dfn[v])
        {
            tarjan(v,i);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<low[v])	//桥的公式qwq
            {
                bridg[i]=bridg[i^1]=1;
            }
        }
        else if(i!=(edge^1))
            low[u]=min(low[u],dfn[v]);
    }
}

因为在一个边双连通分量中，任意两点都存在至少两条互相分离的路径，所以我们可以将其缩为一个点。缩完点之后，我们可以把它转换成一棵树。

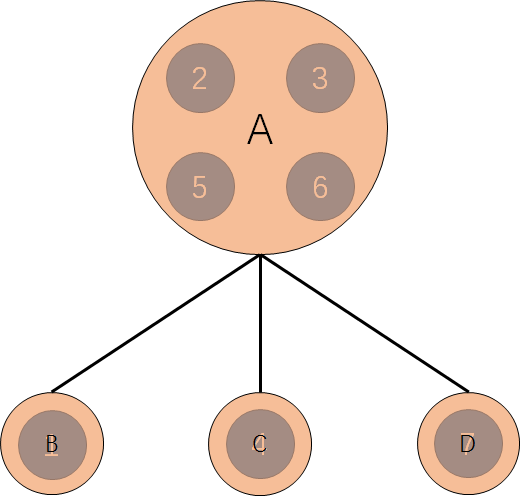
我们会发现，去掉一条边后可能会与原树不连通的，是只连有一条边的边，即叶结点（设其数量为leaf）。为令原图 边双连通（我不知道这么说对不对），我们把两个叶结点为一组用新边将其连接起来。这么看，答案似乎是leaf/2了。

且慢！！让我们看看上图。上图leaf=3，而leaf/2=1。事实上，我们需要2条边。所以最终公式为(leaf+1)/2。（终于完了qwq）

最后捋一捋思路：

• 找边双连通分量

• 缩点

• 建树，找leaf

• ans=(leaf+1)/2

完结撒花qwqwqwqwqwq

code：

//Author:夏目贵志
#include<bits/stdc++.h>
using namespace std;
int qwwq,fst[10100],nex[10100],to[10100],a,b,cnt,num,cutn,bridg[10100],br,u[10100];
int dfn[10100],low[10100],ans,f[10100],root,pl,n,m,size,t,dcc,c[10100],du[10100];
void add(int a,int b)
{
    nex[++t]=fst[a];
    u[t]=a;
    to[t]=b;
    fst[a]=t;
    return ;
}
void tarjan(int u,int edge)
{
    dfn[u]=low[u]=++num;
    for(int i=fst[u];i!=0;i=nex[i])
    {
        int v=to[i];
        if(!dfn[v])
        {
            tarjan(v,i);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<low[v])
            {
                bridg[i]=bridg[i^1]=1;
            }
        }
        else if(i!=(edge^1))
            low[u]=min(low[u],dfn[v]);
    }
}
void dfs(int u)
{
    c[u]=dcc;
    for(int i=fst[u];i!=0;i=nex[i])
    {
        int v=to[i];
        if(c[v]!=0||bridg[i]==1)
        continue;
        dfs(v);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    t=1;
    for(int i=1;i<=m;i++)
    {
     	scanf("%d%d",&a,&b);
     	add(a,b);add(b,a);
    }
    tarjan(1,0);
    for(int i=1;i<=n;i++)
    {
        if(!c[i])
        {
            dcc++;
            dfs(i);
        }
    }
    for(int i=1;i<=m;i++)
    {
     	if(c[u[i*2]]!=c[to[i*2]])
     	{
     		du[c[u[i*2]]]++;
     		du[c[to[i*2]]]++;
     	}
    }
    for(int i=1;i<=dcc;i++)
    {
    	if(du[i]==1)
    	br++;
    }
    cout<<(br+1)/2;

    return 0;
}