Noip模拟51 2021.9.12

T1 茅山道术

考场上卡在了一个恶心的地方，

当时以为每次施法都会产生新的可以施法的区间，然后想都没细想，

认为不可做，甚至$dfs$也无法打，考后一问发现是自己想多了。。

新产生的区间对答案根本没有贡献，还是可以按照原来的相同的颜色搞，

于是无论是$dfs$也好，$dp$也罢，都不用考虑新产生区间的后效性问题

那么我们设$dp_i$表示处理到第$i$个宝石，然后判断一下他的前面有无与他同色的宝石

转移维护前缀和即可。

 1 #include<bits/stdc++.h>//分治+dp?
 2 #define int long long
 3 using namespace std;
 4 namespace AE86{
 5     inline int read(){
 6         int x=0,f=1;char ch=getchar();
 7         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 8         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 9     }inline void write(int x,char opt='\n'){
10         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
11         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
12         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
13 }using namespace AE86;
14
15 const int NN=1e6+5,mod=1e9+7;
16 int n,tot,a[NN],pre[NN];
17 namespace tree_array{
18     int tr[NN];
19     inline int lowbit(int x){return x&(-x);}
20     inline void update(int x,int v){for(int i=x;i<NN;i+=lowbit(i))(tr[i]+=v)%=mod;}
21     inline int query(int x){int ans=0;for(int i=x;i;i-=lowbit(i))(ans+=tr[i])%=mod;return ans;}
22 }using namespace tree_array;
23
24 namespace WSN{
25     inline short main(){
26         freopen("magic.in","r",stdin);
27         freopen("magic.out","w",stdout);
28         n=read();
29         for(int i=1;i<=n;i++) a[i]=read();
30         for(int i=1;i<=n;i++)
31             if(a[i]!=a[i-1]) a[++tot]=a[i];
32         n=tot;update(1,1);
33         for(int i=1;i<=n;i++){
34             if(pre[a[i]]) update(i,query(pre[a[i]]));
35             pre[a[i]]=i;
36         }
37         write(query(n));
38         return 0;
39     }
40 }
41 signed main(){return WSN::main();}

T2 泰拳警告

本场考试最大失误点

考场：

　　$woc$概率题，好像是$dp$，跳了跳了。。。

考后：

　　（看题解），啥？数学？？？？

然后自己五分钟推柿子敲对了就$A$了

还是太弱，无法看出题型。。。太弱了。。。。

不难得出：

$ans= \sum_{i=0}^{n-1} (\frac{1}{p+2})^{n-i} *(\frac{p}{p+2})^i *(n+1) *\sum_{j=0}^{j=\frac{n-i}{2}} C_{n-i}^{j}$

然后发现后面的组合数加和可以轻松的使用杨辉三角每一行的对称性给它搞掉，就注意一下奇偶的细节即可

剩下的都能预处理，不预处理也可以卡过，只不过会拿最劣解（比如我）

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int mod=998244353,NN=3e6+5;
 5 namespace AE86{
 6     inline int read(){
 7         int x=0,f=1;char ch=getchar();
 8         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 9         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
10     }inline void write(int x,char opt='\n'){
11         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
12         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
13         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
14     inline int qmo(int a,int b){
15         if(!a) return 1;
16         int ans=1,c=mod; a%=c;
17         while(b){
18             if(b&1) ans=ans*a%c;
19             b>>=1; a=a*a%c;
20         }
21         return ans;
22     }
23 }using namespace AE86;
24
25 int n,p,inv,ans,v2,tmp,res;
26 int h[NN],v[NN],mi[NN],p1[NN],p2[NN];
27 inline void pre(){
28     h[0]=h[1]=1; v[0]=v[1]=1; mi[0]=p1[0]=p2[0]=1;
29     for(int i=2;i<NN;i++) h[i]=h[i-1]*i%mod;
30     v[NN-1]=qmo(h[NN-1],mod-2);
31     for(int i=NN-2;i>=2;i--) v[i]=v[i+1]*(i+1)%mod;
32     for(int i=1;i<=n;i++){
33         mi[i]=mi[i-1]*2%mod;
34         p1[i]=p1[i-1]*p%mod*inv%mod;
35         p2[i]=p2[i-1]*inv%mod;
36     }
37 }
38 inline int C(int n,int m){
39     if(n<m||n<0||m<0) return 0;
40     return h[n]*v[n-m]%mod*v[m]%mod;
41 }
42
43 namespace WSN{
44     inline short main(){
45         freopen("fight.in","r",stdin);
46         freopen("fight.out","w",stdout);
47         n=read(); p=read(); inv=qmo(p+2,mod-2); v2=qmo(2,mod-2);
48         pre();
49         for(int i=0;i<n;++i){
50             tmp=p1[i]*(i+1)%mod*p2[n-i]%mod*C(n,i)%mod;
51             if((n-i)&1){
52                 res=mi[n-i]*v2%mod;
53                 ans=(ans+tmp*res%mod)%mod;
54             }
55             else{
56                 res=(mi[n-i]-C(n-i,(n-i)/2)+mod)%mod*v2%mod;
57                 ans=(ans+tmp*res%mod)%mod;
58             }
59         }
60         write(ans);
61         return 0;
62     }
63 }
64 signed main(){return WSN::main();}

T3 万猪拱塔

$sb$细节题

考虑枚举权值$[l,r]$的一段区间，将编号在这一段的格子染黑，然后判断黑色是否可以构成一个矩形

我们可以搞出来$(n+1)*(m+1)$ 个$2*2$的小方块覆盖整个矩阵（在边缘外的也算），可以发现：

能够成一个矩形，当且仅当  有$4$个小方块只覆盖$1$个黑格子，没有小方块覆盖恰好$3$个黑格子

要维护$2*2$的小方块：

记$kua[i][5]$为编号为$i$的小方块里面四个格子的权值，因为枚举权值区间的过程是单调递增的

所以将块内的权值排序，这就是他们被染色的顺序，然后按照顺序依次在线段树上$+1，-1$操作即可

设$f(l)$表示在$[l,r]$区间内有多少个小方块包含$1$个或$3$个黑格子，

线段树上维护： $f(l)$的最小值，最小值数目，以及造成最小值的$l$的和。

刚才维护小方块所说的操作就是对最小值的操作

那么最后的答案可以通过维护的值算出。

  1 #include<bits/stdc++.h>
  2 #define int long long
  3 using namespace std;
  4 namespace AE86{
  5     inline int read(){
  6         int x=0,f=1;char ch=getchar();
  7         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
  8         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
  9     }inline void write(int x,char opt='\n'){
 10         char ch[20];int len=0;if(x<0)x=~x+1,putchar('-');
 11         do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
 12         for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);}
 13     inline int max(int a,int b){return a>b?a:b;}
 14     inline int min(int a,int b){return a<b?a:b;}
 15     inline void swap(int &a,int &b){a^=b^=a^=b;}
 16     inline int abs(int x){return x>0?x:-x;}
 17 }using namespace AE86;
 18
 19 const int NN=6e5+5,inf=0x3fffffff,mod=998244353;
 20 int n,m,w[NN],pos[NN],kua[NN][5],pai[5],ans;
 21 struct SNOWtree{
 22     #define lid (id<<1)
 23     #define rid (id<<1|1)
 24     #define mid ((ll[id]+rr[id])>>1)
 25     int ll[NN<<2],rr[NN<<2],laz[NN<<2];
 26     int mss[NN<<2],num[NN<<2],sum[NN<<2];
 27     inline void print(){
 28         for(int i=1;i<=n*m*4;i++) if(ll[i])
 29             printf("l=%lld r=%lld min=%lld num=%lld sum=%lld\n",ll[i],rr[i],mss[i],num[i],sum[i]);
 30     }
 31     inline void pushup(int id){
 32         if(ll[id]==rr[id]) return;
 33         if(mss[lid]==0&&mss[rid]==0) return;
 34         if(mss[lid]==0){mss[id]=mss[rid]; num[id]=num[rid]; sum[id]=sum[rid];return;}
 35         if(mss[rid]==0){mss[id]=mss[lid]; num[id]=num[lid]; sum[id]=sum[lid];return;}
 36         if(mss[rid]==mss[lid]){
 37             mss[id]=mss[lid];
 38             num[id]=num[lid]+num[rid];
 39             sum[id]=sum[lid]+sum[rid];
 40             return;
 41         }
 42         mss[id]=min(mss[lid],mss[rid]);
 43         num[id]=mss[lid]<mss[rid]?num[lid]:num[rid];
 44         sum[id]=mss[lid]<mss[rid]?sum[lid]:sum[rid];
 45         return;
 46     }
 47     inline void pushdown(int id){
 48         if(ll[id]==rr[id]||laz[id]==0) return;
 49         laz[lid]+=laz[id]; laz[rid]+=laz[id];
 50         mss[lid]+=laz[id]; mss[rid]+=laz[id];
 51         laz[id]=0;
 52     }
 53     inline void build(int id,int l,int r){
 54         ll[id]=l; rr[id]=r;
 55         if(l==r){
 56             sum[id]=l; num[id]=1;return;
 57         } int Mid=(l+r)>>1;
 58         build(lid,l,Mid); build(rid,Mid+1,r);
 59     }
 60     inline void update(int id,int l,int r,int v){
 61         if(l<=ll[id]&&rr[id]<=r){
 62             mss[id]+=v; laz[id]+=v;return;
 63         } pushdown(id);
 64         if(l<=mid) update(lid,l,r,v);
 65         if(r>mid) update(rid,l,r,v);
 66         pushup(id);
 67     }
 68     inline void final(int id,int pos){
 69         if(ll[id]==rr[id]) return;
 70         pushdown(id);
 71         if(pos<=mid) final(lid,pos);
 72         else final(rid,pos);
 73         pushup(id);
 74     }
 75     #undef lid
 76     #undef rid
 77     #undef mid
 78 }tr;
 79
 80 inline void update(int r,int pos){
 81     if(kua[pos][1]==inf) return;
 82     if(kua[pos][1]==r){
 83         tr.update(1,1,r,1);
 84     }
 85     if(kua[pos][2]==inf) return;
 86     if(kua[pos][2]==r){
 87         tr.update(1,1,kua[pos][1],-1);
 88         tr.update(1,kua[pos][1]+1,kua[pos][2],1);
 89     }
 90     if(kua[pos][3]==inf) return;
 91     if(kua[pos][3]==r){
 92         tr.update(1,1,kua[pos][1],1);
 93         tr.update(1,kua[pos][1]+1,kua[pos][2],-1);
 94         tr.update(1,kua[pos][2]+1,kua[pos][3],1);
 95     }
 96     if(kua[pos][4]==inf) return;
 97     if(kua[pos][4]==r){
 98         tr.update(1,1,kua[pos][1],-1);
 99         tr.update(1,kua[pos][1]+1,kua[pos][2],1);
100         tr.update(1,kua[pos][2]+1,kua[pos][3],-1);
101         tr.update(1,kua[pos][3]+1,kua[pos][4],1);
102     }
103 }
104 inline int Id(int x,int y){return x*(m+2)+y;}
105 namespace WSN{
106     inline short main(){
107         freopen("pig.in","r",stdin);
108         freopen("pig.out","w",stdout);
109         n=read();m=read(); tr.build(1,1,n*m);
110         for(register int i=1;i<=n;++i) for(register int j=1;j<=m;++j)
111             w[Id(i,j)]=read(),pos[w[Id(i,j)]]=Id(i,j);
112         for(register int i=0;i<=n;++i) for(register int j=0;j<=m;++j){
113             int I1=Id(i,j),I2=Id(i,j+1),I3=Id(i+1,j),I4=Id(i+1,j+1);
114             // cout<<i<<" "<<j<<" "<<I1<<endl;
115             pai[1]=w[I1]; pai[2]=w[I2]; pai[3]=w[I3]; pai[4]=w[I4];
116             for(int k=1;k<=4;k++) if(!pai[k]) pai[k]=inf; sort(pai+1,pai+5);
117             kua[I1][1]=pai[1]; kua[I1][2]=pai[2]; kua[I1][3]=pai[3]; kua[I1][4]=pai[4];
118             // cout<<kua[I1][1]<<" "<<kua[I1][2]<<" "<<kua[I1][3]<<" "<<kua[I1][4]<<endl;
119         }
120         for(register int i=1;i<=n*m;i++){
121             update(i,pos[i]-(m+2)-1);update(i,pos[i]-(m+2));
122             update(i,pos[i]-1);  update(i,pos[i]);
123             tr.final(1,i);
124             // cout<<tr.mss[1]<<" "<<tr.num[1]<<" "<<tr.sum[1]<<endl;
125             if(tr.mss[1]==4) ans=(ans+tr.num[1]*i%mod-tr.sum[1]+tr.num[1]+mod)%mod;
126         }
127         write(ans);
128         return 0;
129     }
130 }
131 signed main(){return WSN::main();}

T4 抑郁刀法

神题，太神了

完全靠数据给出的$m<=n+5$来状压

第一步：删去度数为$1$的点。

发现每次删除一个答案会乘$k-1$，因为他只要和他所链接的那个点颜色不同就行

第二步：转化题意。

题目说是不能让先链接的两个点颜色相同，那么我们在建边的时候每个边新加两个权值$f,g$

表示两个点颜色相同的系数，不同的系数

那么我们输入时所建的边$f=0,g=1$，这样就不用管什么颜色一致与否了。

给出新的题意：

定义一个函数$val(c_i)$表示在第i种合法的染色情况下贡献。那么有：

$val(c_i)=\prod_{e \in \textit{all edge}} \left\{\begin{matrix}f_e (col_i=col_j)\\ g_e (col_i\neq col_j)\end{matrix}\right.$

需要求出$\sum c_i$

第三步：删去度数为$2$的点。

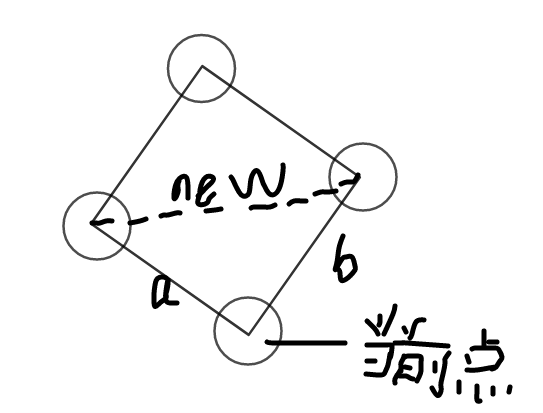
要把当前点删掉，建立一个新的虚边$new$，那么：

1.原本无边，则新边的$newf=(k-1)g_a*g_b+f_a*f_b$

$newg=(k-2)g_a*g_b+f_a*g_b+f_b*g_a$

2.原本又边，那么直接累乘上去即可

第四步：状压$dp$

两步删点后，整张图$n<=10 ,m<=15 $

设$dp[i][j]$表示点集$i$已经染完色，使用了$j$种颜色

枚举一个集合补集的子集$k$

$dp[i|k][j+1]=dp[i][j]*\prod_{k内连边} f * \prod _{集合间连边}g$

为什么直接$+1$，因为如果$k$内有实边那么它一定无法转移，是$0$

所以，上代码

。

。

。

（没写出来姑姑沽）

$UPD 2021.9.19$教练给了自由改题的时间

  1 #include<bits/stdc++.h>
  2 #define int long long
  3 const int NN=1e5+5,mod=1e9+7;
  4 using namespace std;
  5 namespace AE86{
  6     inline int read(){
  7         int x=0,f=1;char ch=getchar();
  8         while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
  9         while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;
 10     }inline int qmo(int a,int b,int ans=1){
 11         int c=mod;while(b){if(b&1) ans=ans*a%c;b>>=1; a=a*a%c;} return ans;
 12     } int h[NN],v[NN];
 13     inline void pre(){
 14         h[0]=h[1]=1; v[0]=v[1]=1;
 15         for(int i=2;i<NN;i++) h[i]=h[i-1]*i%mod;
 16         v[NN-1]=qmo(h[NN-1],mod-2);
 17         for(int i=NN-2;i>=2;i--) v[i]=v[i+1]*(i+1)%mod;
 18     }inline int C(int n,int m){if(n<m||n<0||m<0)return 0;return h[n]*v[n-m]%mod*v[m]%mod;}
 19 }using namespace AE86;
 20
 21 int n,m,k,ans,deg[NN],pw=1;
 22 unordered_map<int,bool> e[NN];
 23 unordered_map<int,int> f[NN],g[NN];
 24 bool vis[NN];
 25 struct node{
 26     int x,d;
 27     bool operator<(const node& x)const{
 28         return d>x.d;
 29     }
 30 }; priority_queue<node> q;
 31 inline void Bfs(){
 32     for(int i=1;i<=n;i++) q.push((node){i,deg[i]});
 33     while(q.size()>1){
 34         node now=q.top(); q.pop();
 35         if(vis[now.x]) continue;
 36         // cout<<now.x<<endl;
 37         int x=now.x;
 38         if(now.d==1){
 39             vis[x]=1; pw=pw*(k-1)%mod;
 40             int y=(*e[x].begin()).first;
 41             --deg[y]; e[y].erase(x); f[y].erase(x); g[y].erase(x);
 42             e[x].clear(); f[x].clear(); g[x].clear(); deg[x]--;
 43             q.push((node){y,deg[y]});
 44         }
 45         else if(now.d==2){
 46             vis[x]=1;
 47             auto it=e[x].begin();
 48             int y1=0,y2=0,f1=0,f2=0,g1=0,g2=0;
 49             if(e[x].size()==1) y1=y2=(*it).first;
 50             else y1=(*it).first, ++it, y2=(*it).first;
 51             if(y1==x&&y2==x){vis[x]=0; continue;}
 52             if(y1==y2){
 53                 if(!e[y1][y1]) f[y1][y1]=1,g[y1][y1]=0;
 54                 f[y1][y1]=f[y1][y1]*(f[x][y1]+(k-1)*g[x][y1]%mod)%mod;
 55             }else{
 56                 f1=f[x][y1],f2=f[x][y2],g1=g[x][y1],g2=g[x][y2];
 57                 if(!e[y1][y2]) f[y1][y2]=f[y2][y1]=g[y1][y2]=g[y2][y1]=1;
 58                 f[y1][y2]=f[y1][y2]*((k-1)*g1%mod*g2%mod+f1*f2%mod)%mod;
 59                 g[y1][y2]=g[y1][y2]*((k-2)*g1%mod*g2%mod+f1*g2%mod+f2*g1%mod)%mod;
 60                 f[y2][y1]=f[y1][y2]; g[y2][y1]=g[y1][y2];
 61             }
 62             e[y1][y2]=e[y2][y1]=1;
 63             e[x].clear(); f[x].clear(); g[x].clear();
 64             e[y1].erase(x); f[y1].erase(x); g[y1].erase(x);
 65             e[y2].erase(x); f[y2].erase(x); g[y2].erase(x);
 66         } else break;
 67     }
 68 }
 69 const int MM=11;
 70 int S[MM],cnt,dp[1<<MM][MM],lg[1<<MM];
 71 int stk[1<<MM],top;
 72 int totf[1<<MM];
 73 unordered_map<int,int> totg[1<<MM];
 74 inline int lowbit(int x){return x&(-x);}
 75 namespace WSN{
 76     inline short main(){
 77         freopen("knife.in","r",stdin);
 78         freopen("knife.out","w",stdout);
 79         n=read();m=read();k=read(); pre();
 80         for(int i=1,x,y;i<=m;i++)
 81             x=read(),y=read(),e[x][y]=e[y][x]=1,f[x][y]=f[y][x]=0,g[x][y]=g[y][x]=1,++deg[x],++deg[y];
 82         Bfs();
 83         /*状压*/
 84         for(int i=1;i<=n;i++) if(!vis[i]) S[cnt++]=i;
 85         for(int i=0;i<cnt;i++) lg[1<<i]=i;
 86         totf[0]=1; int U=(1<<cnt)-1;
 87         for(int i=1;i<=U;i++){
 88             totf[i]=totf[i-lowbit(i)];
 89             int x=lg[lowbit(i)];
 90             for(int j=0;j<cnt;j++) if((i&(1<<j)) && (e[S[x]][S[j]]))
 91                 totf[i]=totf[i]*f[S[x]][S[j]]%mod;
 92         }
 93         for(int i=1;i<=U;i++) totg[0][i]=1;
 94         for(int i=1;i<=U;i++){
 95             totg[i][0]=1;
 96             int T=U^i; top=0;
 97             for(int j=T;j;j=(j-1)&T) stk[top++]=j;//把补集子集放到栈内方便枚举
 98             for(int j=top-1;j>=0;j--){
 99                 int t=stk[j],x=lg[lowbit(t)];
100                 totg[i][t]=totg[i][t-lowbit(t)];
101                 for(int k=0;k<cnt;k++) if((i&(1<<k)) && (e[S[x]][S[k]]))
102                     totg[i][t]=totg[i][t]*g[S[x]][S[k]]%mod;
103             }
104         }
105         dp[0][0]=1;
106         for(int i=0;i<=U;i++) for(int j=0;j<cnt;j++){
107             if(!dp[i][j]) continue;
108             int T=U^i;
109             for(int k=T;k;k=(k-1)&T)
110                 dp[i|k][j+1]=(dp[i|k][j+1]+dp[i][j]*totg[i][k]%mod*totf[k]%mod)%mod;
111         }
112         for(int i=1;i<=cnt;i++) ans=(ans+dp[U][i]*C(k,i)%mod)%mod;
113         printf("%lld\n",ans*pw%mod);
114         return 0;
115     }
116 }
117 signed main(){return WSN::main();}

确实有很多细节，然后就是那个转移之前要预处理，注意边界赋值就好