【数据结构与算法Python版学习笔记】树——利用二叉堆实现优先级队列

概念

• 队列有一个重要的变体，叫作优先级队列。
  • 和队列一样，优先级队列从头部移除元素，不过元素的逻辑顺序是由优先级决定的。
  • 优先级最高的元素在最前，优先级最低的元素在最后。
• 实现优先级队列的经典方法是使用叫作二叉堆(Binary Heap)的数据结构。
  • 二叉堆的入队操作和出队操作均可达到O(log n)。
  • 其逻辑结构上像二叉树， 却是用非嵌套的列表来实现的
  • 二叉堆有两个常见的变体：
    • 最小堆（最小的元素一直在队首）
    • 最大堆（最大的元素一直在队首）

二叉堆的操作

• BinaryHeap()新建一个空的二叉堆。

• insert(k)往堆中加入一个新元素。

• findMin()返回最小的元素，元素留在堆中。

• delMin()返回最小的元素，并将该元素从堆中移除。

• isEmpty()在堆为空时返回True，否则返回False。

• size()返回堆中元素的个数。

• buildHeap(list)根据一个列表创建堆。

用非嵌套列表实现二叉堆

结构属性

• 为了使堆操作能保持在对数水平上， 就必须采用二叉树结构；
• 同样， 如果要使操作始终保持在对数数量级上， 就必须始终保持二叉树的“平衡”
  • 树根左右子树拥有相同数量的节点
  • 我们采用“完全二叉树”的结构来近似实现“平衡”
    
    完全二叉树，叶节点最多只出现在最底层和次底层，而且最底层的叶节点都连续集中在最左边，每个内部节点都有两个子节点， 最多可有1个节点例外
    • 下标为p
    • 左子节点下标为2p
    • 右子节点为2p+1
    • 父节点下标为p//2

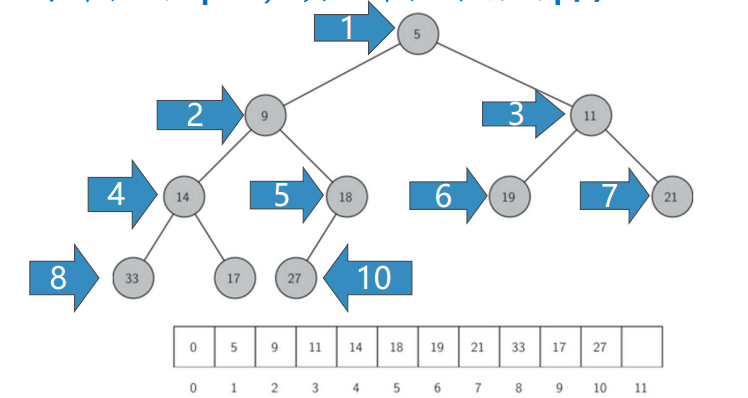
堆次序 Heap Order

• 任何一个节点x， 其父节点p中的key均小于x中的key
  
  这样，符合“堆”性质的二叉树，其中任何一条路径，均是一个已排序数列， 根节点的key最小

二叉堆操作的实现

二叉堆初始化

• 采用一个列表来保存堆数据，其中表首下标为0的项无用，但为了后面代码可以用到简单的整数乘除法，仍保留它。

class BinHeap:
    def __init__(self):
        self.heapList=[0]
        self.currentSize=0

insert(key)方法

• 新key加在列表末尾，显然无法保持“堆”次序虽然对其它路径的次序没有影响，但对于其到根的路径可能破坏次序
• 需要将新key沿着路径来“上浮”到其正确位置
• 注意：新key的“上浮”不会影响其它路径节点的“堆”次序

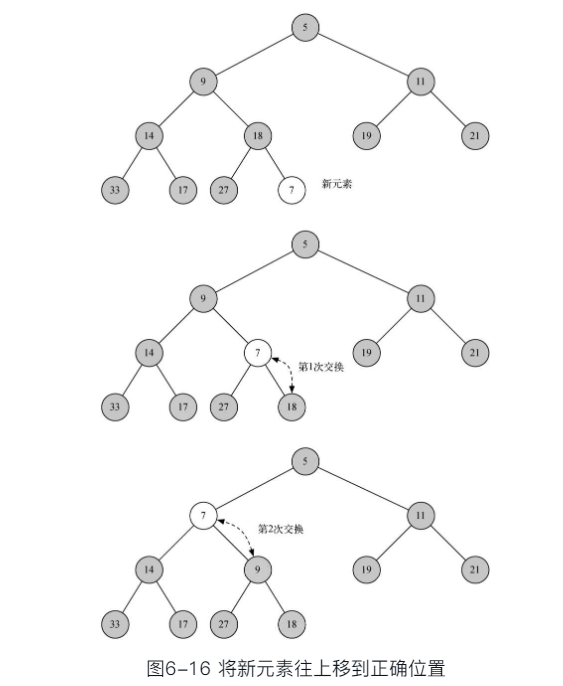
# 上浮
    def percUp(self, i):
        while i//2 > 0:
            if self.heapList[i] < self.heapList[i//2]:
                self.heapList[i], self.heapList[i //
                                                2] = self.heapList[i//2], self.heapList[i]
            i = i//2

    def insert(self, k):
        self.heapList.append(k)
        self.currentSize += 1
        self.percUp(self.currentSize)

delMin()方法

• 移走整个堆中最小的key:根节点heapList[1]
• 为了保持“完全二叉树”的性质，只用最后一个节点来代替根节点.
  • 将新的根节点沿着一条路径“下沉”，直到比两个子节点都小
  • “下沉”路径的选择：如果比子节点大，那么选择较小的子节点交换下沉

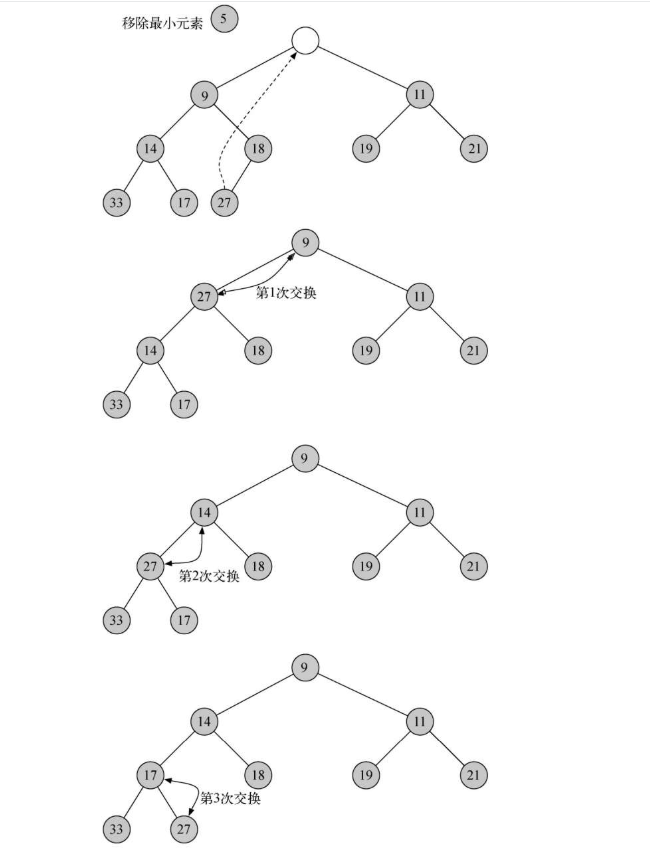
def percDown(self, i):
        while(i*2) <= self.currentSize:
            mc = self.minChild(i)
            if self.heapList[i] > self.heapList(mc):
                self.heapList[i], self.heapList[mc] = self.heapList[mc], self.heapList[i]
            i = mc

    def minChild(self, i):
        if i*2+1 > self.currentSize:
            return i*2
        else:
            if self.heapList[i*2] < self.heapList[i*2+1]:
                return i*2
            else:
                return i*2+1

    def delMin(self):
        retval = self.heapList[1]
        self.heapList[1] = self.heapList[self.currentSize]
        self.currentSize -= 1
        self.heapList.pop()
        self.percDown(1)
        return retval

buildHeap(lst)方法：从无序表生成“堆”

• 用insert(key)方法，将无序表中的数据项逐个insert到堆中，但这么做的总代价是O(nlog n)
• 其实，用“下沉”法，能够将总代价控制在O(n)

def buildHeap(self, alist):
        i = len(alist)//2
        self.currentSize = len(alist)
        self.heapList = [0]+alist[:]
        print(len(self.heapList), i)
        while(i > 0):
            print(self.heapList, i)
            self.percDown(i)
            i -= 1
        print(self.heapList, i)

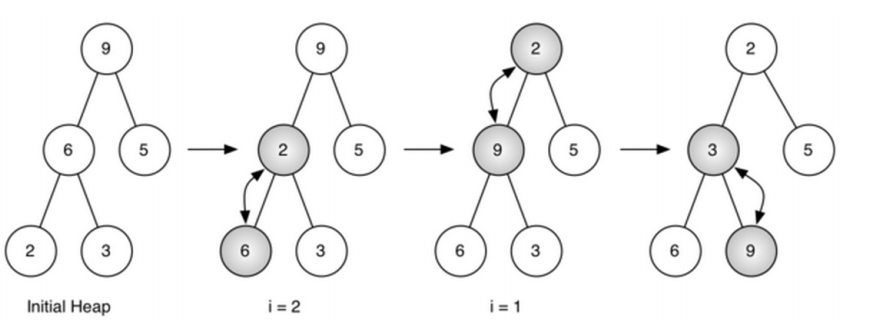
堆排序

• “堆排序”算法： O(nlog n)

二叉堆列表实现完整代码

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0

    # 上浮
    def percUp(self, i):
        while i//2 > 0:
            if self.heapList[i] < self.heapList[i//2]:
                self.heapList[i], self.heapList[i //
                                                2] = self.heapList[i//2], self.heapList[i]
            i = i//2

    def insert(self, k):
        self.heapList.append(k)
        self.currentSize += 1
        self.percUp(self.currentSize)

    def percDown(self, i):
        while(i*2) <= self.currentSize:
            mc = self.minChild(i)
            if self.heapList[i] > self.heapList(mc):
                self.heapList[i], self.heapList[mc] = self.heapList[mc], self.heapList[i]
            i = mc

    def minChild(self, i):
        if i*2+1 > self.currentSize:
            return i*2
        else:
            if self.heapList[i*2] < self.heapList[i*2+1]:
                return i*2
            else:
                return i*2+1

    def delMin(self):
        retval = self.heapList[1]
        self.heapList[1] = self.heapList[self.currentSize]
        self.currentSize -= 1
        self.heapList.pop()
        self.percDown(1)
        return retval

    def buildHeap(self, alist):
        i = len(alist)//2
        self.currentSize = len(alist)
        self.heapList = [0]+alist[:]
        print(len(self.heapList), i)
        while(i > 0):
            print(self.heapList, i)
            self.percDown(i)
            i -= 1
        print(self.heapList, i)