Python数模笔记-（1）NetworkX 图的操作

1、NetworkX 图论与网络工具包

NetworkX 是基于 Python 语言的图论与复杂网络工具包，用于创建、操作和研究复杂网络的结构、动力学和功能。

NetworkX 可以以标准和非标准的数据格式描述图与网络，生成图与网络，分析网络结构，构建网络模型，设计网络算法，绘制网络图形。

NetworkX 提供了图形的类、对象、图形生成器、网络生成器、绘图工具，内置了常用的图论和网络分析算法，可以进行图和网络的建模、分析和仿真。

NetworkX 的官网和文档

官网地址：https://networkx.org/

官方文档： https://networkx.org/documentation/stable/

pdf 文档：　https://networkx.org/documentation/stable/_downloads/networkx_reference.pdf

NetworkX 的安装

NetworkX 的安装要求：Python 3.2 以上版本，推荐安装 NumPy、SciPy、Matplotlib、Graphviz 工具包的支持。

pip 安装：

　　

pip3 install networkx

pip3 install networkx -i https://mirrors.aliyun.com/pypi/simple

本系列写作计划

NetworkX 的功能非常强大和庞杂，所涉及内容远远、远远地超出了数学建模的范围，甚至于花了很长时间还不能对其进行比较系统的概括。

本系列以数模学习和应用的需求为主线，介绍相关的基本功能和典型算法的应用。

　　

=== 关注 Youcans 原创系列（https://www.cnblogs.com/youcans/）

2、图、顶点和边的创建与基本操作

图由顶点和连接顶点的边构成，但与顶点的位置、边的曲直长短无关。

图提供了一种处理关系和交互等抽象概念的更好的方法，它还提供了直观的视觉方式来思考这些概念。

Networkx支持创建简单无向图、有向图和多重图（multigraph）；内置许多标准的图论算法，节点可为任意数据；支持任意的边值维度，功能丰富，简单易用。

2.1 图的基本概念

图（Graph）。若干点和一些连接这些点的连线，所构成关系结构就是一个图。
顶点（Node）和边（Edge）。图中的点称为顶点，也称节点。两个顶点之间的连线，称为边。
平行边（Parallel edge）和循环（Cycle）。起点相同、终点也相同的两条边称为平行边。起点和终点重合的边称为循环。
有向图（Digraph）和无向图（Undirected graph）。图中的每条边都带有方向，称为有向图；图中的每条边都没有方向，称为无向图；有的边带有方向，有的边没有方向，称为混合图。
赋权图（Weighted graph）。图中的每条边都有一个或多个对应的参数，称为赋权图。该参数称为这条边的权，权可以用来表示两点间的距离、时间、费用。
度（Degree）。与顶点相连的边的数量，称为该顶点的度。

2.2 图、顶点和边的操作

Networkx很容易创建图、向图中添加顶点和边、从图中删除顶点和边，也可以查看、删除顶点和边的属性。

图的创建

Graph()类、DiGraph()类、MultiGraph()类和MultiDiGraph() 类分别用来创建无向图、有向图、多图和有向多图。

class Graph(incoming_graph_data=None, **attr)

import networkx as nx

import networkx as nx  # 导入 NetworkX 工具包

# 创建 图

G1 = nx.Graph()  # 创建：空的 无向图

G2 = nx.DiGraph()  #创建：空的 有向图

G3 = nx.MultiGraph()  #创建：空的 多图

G4 = nx.MultiDiGraph()  #创建：空的 有向多图

顶点的添加、删除和查看

图的每个顶点都有唯一的标签属性（label），可以用整数或字符类型表示，顶点还可以自定义任意属性。

顶点的常用操作：添加顶点，删除顶点，定义顶点属性，查看顶点和顶点属性。

# 顶点(node)的操作

G1.add_node(1)  # 向 G1 添加顶点 1

G1.add_node(1,name='n1',weight=1.0)  # 添加顶点 1，定义 name, weight 属性

G1.add_node(2,date='May-16') # 添加顶点 2，定义 time 属性

G1.add_nodes_from([3, 0, 6], dist=1)  # 添加多个顶点：3，0，6

# 查看顶点和顶点属性

print(G1.nodes())  # 查看顶点

# [1, 2, 3, 0, 6]

print(G1._node)  # 查看顶点属性

# {1: {'name': 'n1', 'weight': 1.0}, 2: {'date': 'May-16'}, 3: {'dist': 1}, 0: {'dist': 1}, 6: {'dist': 1}}

H = nx.path_graph(8)  # 创建 路径图 H：由 n个节点、n-1条边连接，节点标签为 0 至 n-1

G1.add_nodes_from(H)  # 由路径图 H 向图 G1 添加顶点 0～9

print(G1.nodes())  # 查看顶点

# [1, 2, 3, 0, 6, 4, 5, 7]  # 顶点列表

G1.add_nodes_from(range(10, 15))  # 向图 G1 添加顶点 10～14

print(G1.nodes())  # 查看顶点

# [1, 2, 3, 0, 6, 4, 5, 7, 10, 11, 12, 13, 14]

# 从图中删除顶点

G1.remove_nodes_from([1, 11, 13, 14])  # 通过顶点标签的 list 删除多个顶点

print(G1.nodes())  # 查看顶点

# [2, 3, 0, 6, 4, 5, 7, 10, 12]  # 顶点列表

# === 关注 Youcans 原创系列（https://www.cnblogs.com/youcans/）

边的添加、删除和查看

边是两个顶点之间的连接，在 NetworkX 中用边是由对应顶点的名字的元组组成 e=(node1,node2)。边可以设置权重、关系等属性。

边的常用操作：添加边，删除边，定义边的属性，查看边和边的属性。向图中添加边时，如果添加的边的顶点是图中不存在的，则自动向图中添加该顶点。

# 边(edge)的操作

G1.add_edge(1,5)  # 向 G1 添加边 1-5，并自动添加图中没有的顶点

G1.add_edge(0,10, weight=2.7)  # 向 G1 添加边 0-10，并设置属性

G1.add_edges_from([(1,2,{'weight':0}), (2,3,{'color':'blue'})])  # 向图中添加边，并设置属性

print(G1.nodes())  # 查看顶点

# [2, 3, 0, 6, 4, 5, 7, 10, 12, 1]  # 自动添加了图中没有的顶点 1

G1.add_edges_from([(3,6),(1,2),(6,7),(5,10),(0,1)])  # 向图中添加多条边

G1.add_weighted_edges_from([(1,2,3.6),[6,12,0.5]])  # 向图中添加多条赋权边: (node1,node2,weight)

G1.remove_edge(0,1)  # 从图中删除边 0-1

# G1.remove_edges_from([(2,3),(1,5),(6,7)])  # 从图中删除多条边

# print(G1.edges(data=True))  # 查看所有边的属性

print(G1.edges)  # 查看所有边

# [(2, 1), (2, 3), (3, 6), (0, 10), (6, 7), (6, 12), (5, 1), (5, 10)]

print(G1.get_edge_data(1,2))  # 查看指定边 1-2 的属性

# {'weight': 3.6}

print(G1[1][2])  # 查看指定边 1-2 的属性

# {'weight': 3.6}

查看图、顶点和边的信息

print(G1.nodes)  # 返回所有的顶点 [node1,...]

# [1, 2, 0, 6, 4, 12, 5, 9, 8, 3, 7]

print(G1.edges)  # 返回所有的边 [(node1,node2),...]

# [(1,5), (1,2), (2,8), (2,3), (0,9), (6,5), (6,7), (6,12), (4,3), (4,5), (9,8), (8,7)]

print(G1.degree)  # 返回各顶点的度 [(node1,degree1),...]

# [(1,2), (2,3), (0,1), (6,3), (4,2), (12,1), (5,3), (9,2), (8,3), (3,2), (7,2)]

print(G1.number_of_nodes())  # 返回所有的顶点 [node1,...]

# 11

print(G1.number_of_edges())  # 返回所有的顶点 [node1,...]

# 12

print(G1[2])  # 返回指定顶点相邻的顶点和顶点的属性

# {1: {'weight': 3.6}, 8: {'color': 'blue'}, 3: {}}

print(G1.adj[2])  # 返回指定顶点相邻的顶点和顶点的属性

# {1: {'weight': 3.6}, 8: {'color': 'blue'}, 3: {}}

print(G1[6][12])  # 返回指定边的属性

# {'weight': 0.5}

print(G1.adj[6][12])  # 返回指定边的属性

# {'weight': 0.5}

print(G1.degree(5))  # 返回指定顶点的度

# 3

print('nx.info:',nx.info(G1))  # 返回图的基本信息

print('nx.degree:',nx.degree(G1))  # 返回图中各顶点的度

print('nx.density:',nx.degree_histogram(G1))  # 返回图中度的分布

print('nx.pagerank:',nx.pagerank(G1))  # 返回图中各顶点的频率分布

2.3 图的属性和方法

图的方法

方法	说明
G.has_node(n)	当图 G 中包括顶点 n 时返回 True
G.has_edge(u, v)	当图 G 中包括边 (u,v) 时返回 True
G.number_of_nodes()	返回图 G 中的顶点的数量
G.number_of_edges()	返回图 G 中的边的数量
G.number_of_selfloops()	返回图 G 中的自循环边的数量
G.degree([nbunch, weight])	返回图 G 中的全部顶点或指定顶点的度
G.selfloop_edges([data, default])	返回图 G 中的全部的自循环边
G.subgraph([nodes])	从图 G1中抽取顶点[nodes]及对应边构成的子图
union(G1,G2)	合并图 G1、G2
nx.info(G)	返回图的基本信息
nx.degree(G)	返回图中各顶点的度
nx.degree_histogram(G)	返回图中度的分布
nx.pagerank(G)	返回图中各顶点的频率分布
nx.add_star(G,[nodes],**attr)	向图 G 添加星形网络
nx.add_path(G,[nodes],**attr)	向图 G 添加一条路径
nx.add_cycle(G,[nodes],**attr)	向图 G 添加闭合路径

例程：

# Copyright 2021 YouCans, XUPT

G1.clear() # 清空图G1

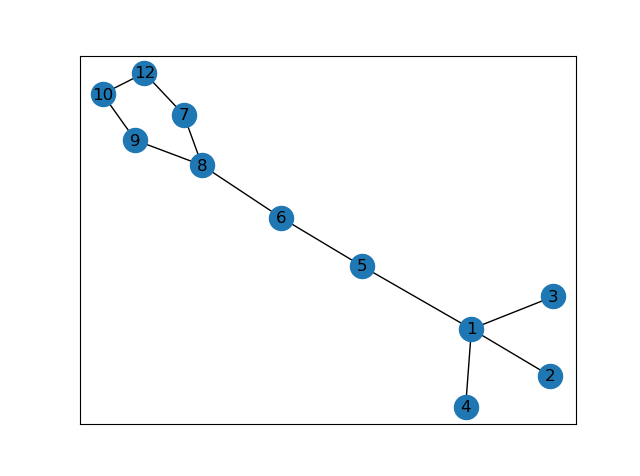
nx.add_star(G1, [1, 2, 3, 4, 5], weight=1)  # 添加星形网络：以第一个顶点为中心

# [(1, 2), (1, 3), (1, 4), (1, 5)]

nx.add_path(G1, [5, 6, 8, 9, 10], weight=2)  # 添加路径：顺序连接 n个节点的 n-1条边

# [(5, 6), (6, 8), (8, 9), (9, 10)]

nx.add_cycle(G1, [7, 8, 9, 10, 12], weight=3)  # 添加闭合回路：循环连接 n个节点的 n 条边

# [(7, 8), (7, 12), (8, 9), (9, 10), (10, 12)]

print(G1.nodes)  # 返回所有的顶点 [node1,...]

nx.draw_networkx(G1)

plt.show()

G2 = G1.subgraph([1, 2, 3, 8, 9, 10])

G3 = G1.subgraph([4, 5, 6, 7])

G = nx.union(G2, G3)

print(G.nodes)  # 返回所有的顶点 [node1,...]

# [1, 2, 3, 8, 9, 10, 4, 5, 6, 7]

3、图的绘制与分析

3.1 图的绘制

可视化是图论和网络问题中很重要的内容。NetworkX 在 Matplotlib、Graphviz 等图形工具包的基础上，提供了丰富的绘图功能。

本系列拟对图和网络的可视化作一个专题，在此只简单介绍基于 Matplotlib 的基本绘图函数。基本绘图函数使用字典提供的位置将节点放置在散点图上，或者使用布局函数计算位置。

方法	说明
draw(G[,pos,ax])	基于 Matplotlib 绘制图 G
draw_networkx(G[, pos, arrows, with_labels])	基于 Matplotlib 绘制图 G
draw_networkx_nodes(G, pos[, nodelist, . . . ])	绘制图 G 的顶点
draw_networkx_edges(G, pos[, edgelist, . . . ])	绘制图 G 的边
draw_networkx_labels(G, pos[, labels, . . . ])	绘制顶点的标签
draw_networkx_edge_labels(G, pos[, . . . ])	绘制边的标签

其中，nx.draw() 和 nx.draw_networkx() 是最基本的绘图函数，并可以通过自定义函数属性或其它绘图函数设置不同的绘图要求。常用的属性定义如下：

'node_size'：指定节点的尺寸大小，默认300
'node_color'：指定节点的颜色，默认红色
'node_shape'：节点的形状，默认圆形
''alpha'：透明度，默认1.0，不透明
'width'：边的宽度，默认1.0
'edge_color'：边的颜色，默认黑色
'style'：边的样式，可选 'solid'、'dashed'、'dotted'、'dashdot'
'with_labels'：节点是否带标签，默认True
'font_size'：节点标签字体大小，默认12
'font_color'：节点标签字体颜色，默认黑色

3.2 图的分析

NetwotkX 提供了图论函数对图的结构进行分析：

子图

子图是指顶点和边都分别是图 G 的顶点的子集和边的子集的图。

subgraph()方法，按顶点从图 G 中抽出子图。例程如前。

连通子图

如果图 G 中的任意两点间相互连通，则 G 是连通图。

connected_components()方法，返回连通子图的集合。

G = nx.path_graph(4)

nx.add_path(G, [7, 8, 9])

# 连通子图

listCC = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)]

maxCC = max(nx.connected_components(G), key=len)

print('Connected components:{}'.format(listCC))  # 所有连通子图

# Connected components:[4, 3]

print('Largest connected components:{}'.format(maxCC))  # 最大连通子图

# Largest connected components:{0, 1, 2, 3}

** 强连通**

如果有向图 G 中的任意两点间相互连通，则称 G 是强连通图。

strongly_connected_components()方法，返回所有强连通子图的列表。

# 强连通

G = nx.path_graph(4, create_using=nx.DiGraph())

nx.add_path(G, [3, 8, 1])

# 找出所有的强连通子图

con = nx.strongly_connected_components(G)

print(type(con),list(con))

# <class 'generator'> [{8, 1, 2, 3}, {0}]

弱连通

如果一个有向图 G 的基图是连通图，则有向图 G 是弱连通图。

weakly_connected_components()方法，返回所有弱连通子图的列表。

# 弱连通

G = nx.path_graph(4, create_using=nx.DiGraph())  #默认生成节点 0,1,2,3 和有向边 0->1,1->2,2->3

nx.add_path(G, [7, 8, 3])  #生成有向边：7->8->3

con = nx.weakly_connected_components(G)

print(type(con),list(con))

# <class 'generator'> [{0, 1, 2, 3, 7, 8}]

=== 关注 Youcans 原创系列（https://www.cnblogs.com/youcans/）

版权说明：

参考文献声明：本文部分内容参考了 NetworkX 官网介绍：https://networkx.org/documentation/stable/

YouCans 原创作品

Copyright 2021 YouCans, XUPT

Crated：2021-05-16