普里姆（Prim）算法
概览
普里姆算法（Prim算法），图论中的一种算法，可在加权连通图（即“带权图”）里搜索最小生成树。即此算法搜索到的边（Edge）子集所构成的树中，不但包括了连通图里的所有顶点（Vertex）且其所有边的权值之和最小。
（注：N个顶点的图中，其最小生成树的边为N-1条，且各边之和最小。树的每一个节点（除根节点）有且只有一个前驱，所以，只有N-1条边。）
该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。
定义
假设G=(V, {E})是连通网，TE是N上最小生成树中边（Edge）的集合。V是图G的顶点的集合，E是图G的边的集合。算法从U={u0} (u0∈V)，TE={}开始。重复执行下述操作：
- 在所有u∈U，v∈V-U的边(u, v)∈E中找一条代价（权值）最小的边(u0, v0)并入集合TE。
- 同时v0并入U
- 直至U=V为止。此时TE中必有n-1条边，则T=(V, {TE})为N的最小生成树。
由算法代码中的循环嵌套可得知此算法的时间复杂度为O(n2)。
过程简述
输入：带权连通图（即“网”）G，其顶点的集合为V，边的集合为E。
初始：U={u}，u为从V中任意选取顶点，作为起始点；TE={}。
操作：重复以下操作，直到U=V，即两个集合相等。
- 在集合E中选取权值最小的边(u, v)，u∈U，v∈V且v∉U。（如果存在多条满足前述条件，即权值相同的边，则可任意选取其中之一。）
- 将v并入U，将(u, v)边加入TE。
输出：用集合U和TE来描述所得到的最小生成树。
如何实现
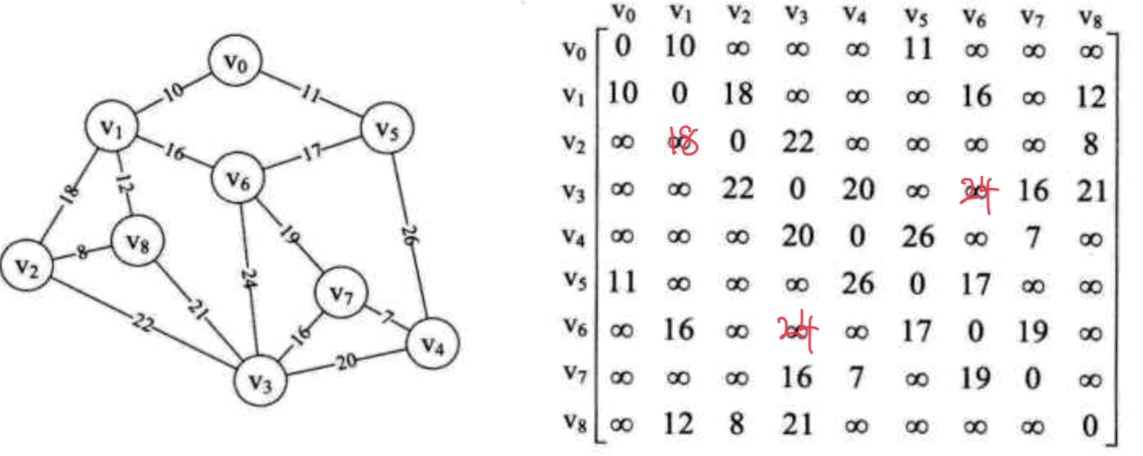
如上面的这个图G=(V, {E})，其中：
V={v0, v1, v2, v3, v4, v5, v6, v7, v8}，
E= {(v0, v1), (v0, v5), (v1, v6), (v5, v6), (v1, v8), (v1, v2), (v2, v8), (v6, v7), (v3, v6), (v4, v5), (v4, v7), (v3, v7), (v3, v4), (v3,v8), (v2, v3)}
用邻接矩阵表示该图G，得上图右边的邻接矩阵。
此图G有n = 9个顶点，其最小生成树则必有n-1 = 8条边。
（注意：图G的最小生成树是一棵树，且图G中的每个顶点都在这棵树里，故必含有n个顶点；而除树根节点，每个节点有且只有一个前驱，所以图G的最小生成树有且只有n-1条边。若边数大于n-1，则必有树中某个顶点与另一个顶点存在第二条边，从而不能构成树。树中节点是一对多关系而不是多对多关系。）
①输入：带权连通图G=(V, {E})，求图G的最小生成树。
②初始：U={u}，取图G中的v0作为u，用数组adjVex=int[9]来表示U（最终U要等于V），adjVex数组记录的是U中顶点的下标。U是最小生成树T的各边的起始顶点的集合。
adjVex初始值为[0, 0, 0, 0, 0, 0, 0, 0, 0]，表示从顶点v0开始去寻找权值最小的边。
用数组lowCost = int[9] 表示adjVex中各点到集合V中顶点构成的边的权值。lowCost数组中元素的索引即是顶点V的下标。解释：adjVex[3] == 0，表示v0，adjVex[5] == 0，表示v0。lowCost[3] == ∞且adjVex[3] == 0，表示(v0, v3)边不存在；lowCost[5] == 11且adjVex[5] == 0，表示(v0, v5)边的权值为11。
如：邻接矩阵中的v0行，v0顶点与各顶点构成的边及其权值用下面这的方式表示：
示例一
索引：index [0, 1, 2, 3, 4, 5, 6, 7, 8]
权值：lowCost[0, 10, ∞, ∞, ∞, 11, ∞, ∞, ∞]
下标：adjVex [0, 0, 0, 0, 0, 0, 0, 0, 0](v0, v0, 0), (v0, v3, ∞), (v0, v5, 11)
0表示以该顶点为终点的边已经并入图G的最小生成树的边集合——TE集合，不需要再比较（搜索）。
∞表示以该顶点为终点的边不存在。
③操作：
- 上面示例一中，最小的权值为10，此时lowCost中下标k = 1，相应地adjVex[k]即adjVex[1] == 0，记录下此时的边为(v0, v1)。
- 将adjVex[k]即adjVex[1]设为1，表示将顶点v1放入图G的最小生成树的顶点集合U中。
- 将lowCost[k]即lowCost[1]设为0，表示以v1为终止点的边已搜索。
- 然后，将焦点转向顶点v1，看看从v1开始的边有哪些是权值小于从之前的顶点v0开始的边的。此时k == 1。则有以下过程：
索引：index [ 0, 1, 2, 3, 4, 5, 6, 7, 8]
权值：lowCost[ 0, 0, ∞, ∞, ∞, 11, ∞, ∞, ∞]
下标：adjVex [ 0, 1, 0, 0, 0, 0, 0, 0, 0]
顶点：vex[1] [10, 0,18, ∞, ∞, ∞,16, ∞,12]
由于lowCost[0]和lowCost[1]为0，所以从lowCost[2]开始比较权值。vex[1][2] == 18 < lowCost[2]，意思是(v0, v2)==∞不存在这条边，(v1, v2) == 18，存在权为18的边(v1, v2)，类似的还有vex[1][6] == 16 < lowCost[6]和vex[1][8] == 12 < lowCost[8]。
把k == 1赋值给
adjVex[2]、adjVex[6]和adjVex[8]。
把权值18、16和12赋值给
lowCost[2]、lowCost[6]和lowCost[8]。
更新后的权值数组和邻接顶点数组如下：
索引：index [ 0, 1, 2, 3, 4, 5, 6, 7, 8]
权值：lowCost[ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12]
下标：adjVex [ 0, 1, 1, 0, 0, 0, 1, 0, 1]
故下次循环从顶点v1为起点去搜索lowCost中权值最小的边。如此往复循环，直到图G中的每一个顶点都被遍历到。（邻接矩阵的每一行都被遍历到）
④输出：
演示过程
Loop 1
lowCost: [ 0, 10, ∞, ∞, ∞, 11, ∞, ∞, ∞ ]
adjVex: [ 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
lowCost: [ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12 ]
adjVex: [ 0, 1, 1, 0, 0, 0, 1, 0, 1 ]
Loop 2
lowCost: [ 0, 0, 18, ∞, ∞, 11, 16, ∞, 12 ]
adjVex: [ 0, 1, 1, 0, 0, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 18, ∞, 26, 0, 16, ∞, 12 ]
adjVex: [ 0, 1, 5, 0, 5, 0, 1, 0, 1 ]
Loop 3
lowCost: [ 0, 0, 18, ∞, 26, 0, 16, ∞, 12 ]
adjVex: [ 0, 1, 5, 0, 5, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 8, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 5, 0, 1, 0, 1 ]
Loop 4
lowCost: [ 0, 0, 8, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 5, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 0, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 0, 1, 0, 1 ]
Loop 5
lowCost: [ 0, 0, 0, 21, 26, 0, 16, ∞, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 0, 1, 0, 1 ]
lowCost: [ 0, 0, 0, 21, 26, 0, 0, 19, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 6, 1, 6, 1 ]
Loop 6
lowCost: [ 0, 0, 0, 21, 26, 0, 0, 19, 0 ]
adjVex: [ 0, 1, 8, 8, 2, 6, 1, 6, 1 ]
lowCost: [ 0, 0, 0, 16, 7, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 6, 1 ]
Loop 7
lowCost: [ 0, 0, 0, 16, 7, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 6, 1 ]
lowCost: [ 0, 0, 0, 16, 0, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 4, 1 ]
Loop 8
lowCost: [ 0, 0, 0, 16, 0, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 4, 1 ]
lowCost: [ 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
adjVex: [ 0, 1, 8, 7, 7, 6, 7, 4, 3 ]
运行结果
(0, 1)
(0, 5)
(1, 8)
(8, 2)
(1, 6)
(6, 7)
(7, 4)
(7, 3)
算法代码
C#代码
using System;
namespace Prim
{
class Program
{
static void Main(string[] args)
{
int numberOfVertexes = 9,
infinity = int.MaxValue;
int[][] graph = new int[][] {
new int[]{0, 10, infinity, infinity, infinity, 11, infinity, infinity, infinity },
new int[]{ 10, 0, 18, infinity, infinity, infinity, 16, infinity, 12 },
new int[]{ infinity, 18, 0, 22, infinity, infinity, infinity, infinity, 8 },
new int[]{ infinity, infinity, 22, 0, 20, infinity, 24, 16, 21 },
new int[]{ infinity, infinity, infinity, 20, 0, 26, infinity, 7, infinity },
new int[]{ 11, infinity, infinity, infinity, 26, 0, 17, infinity, infinity },
new int[]{ infinity, 16, infinity, 24, infinity, 17, 0, 19, infinity },
new int[]{ infinity, infinity, infinity, 16, 7, infinity, 19, 0, infinity },
new int[]{ infinity, 12, 8, 21, infinity, infinity, infinity, infinity, 0 },
};
//Prim(graph, numberOfVertexes);
PrimSimplified(graph, numberOfVertexes);
}
static void Prim(int[][] graph, int numberOfVertexes)
{
bool debug = true;
int[] adjVex = new int[numberOfVertexes], // 邻接顶点数组：搜索边的最小权值过程中各边的起点坐标
lowCost = new int[numberOfVertexes]; // 各边权值数组：搜索边的最小权值过程中各边的权值，数组下标为边的终点。
for (int i = 0; i < numberOfVertexes; i++) // 从图G的下标为0的顶点开始搜索。（也是图G的最小生成树的顶点集合）。
{
adjVex[i] = 0;
}
for (int i = 0; i < numberOfVertexes; i++) // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
{
lowCost[i] = graph[0][i];
}
int k = 0; // 初始假定权值最小的边的终点的下标为k。
for (int i = 1; i < numberOfVertexes; i++)
{
if (debug)
{
Console.WriteLine($"Loop {i}");
Console.Write("lowCost: ");
PrintArray(lowCost);
Console.Write(" adjVex: ");
PrintArray(adjVex);
Console.WriteLine();
}
int minimumWeight = int.MaxValue; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (int j = 1; j < numberOfVertexes; j++)
{
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
if (!debug)
{
Console.WriteLine($"({adjVex[k]}, {k})"); // 输出边
}
adjVex[i] = k; // 此时找到的k值即是权值最小的边的终点。将V[k]放入集合U。（这步可省略，因lowCost[j]已被标为“无需搜索”了）。
lowCost[k] = 0; // 0表示该点已经搜索过了，已不需要再被搜索了。
for (int j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边，去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值；索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时，从k为下标的顶点为起点。
}
}
if (debug)
{
Console.Write("lowCost: ");
PrintArray(lowCost);
Console.Write(" adjVex: ");
PrintArray(adjVex);
Console.WriteLine();
}
}
}
static void PrimSimplified(int[][] graph, int numberOfVertexes)
{
int[] adjVex = new int[numberOfVertexes], // 邻接顶点数组：搜索边的最小权值过程中各边的起点坐标
lowCost = new int[numberOfVertexes]; // 各边权值数组：搜索边的最小权值过程中各边的权值，数组下标为边的终点。
for (int i = 0; i < numberOfVertexes; i++)
{
adjVex[i] = 0; // 从图G的下标为0的顶点开始搜索。（也是图G的最小生成树的顶点集合）。
lowCost[i] = graph[0][i]; // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
}
int k = 0; // 初始假定权值最小的边的终点的下标为k。
for (int i = 1; i < numberOfVertexes; i++)
{
int minimumWeight = int.MaxValue; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (int j = 1; j < numberOfVertexes; j++)
{
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
Console.WriteLine($"({adjVex[k]}, {k})"); // 输出边
lowCost[k] = 0; // 0表示该点已经搜索过了，已不需要再被搜索了。
for (int j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边，去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值；索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时，从k为下标的顶点为起点。
}
}
}
}
static void PrintArray(int[] array)
{
Console.Write("[ ");
for (int i = 0; i < array.Length - 1; i++) // 输出数组的前面n-1个
{
Console.Write($"{ToInfinity(array[i])}, ");
}
if (array.Length > 0) // 输出数组的最后1个
{
int n = array.Length - 1;
Console.Write($"{ToInfinity(array[n])}");
}
Console.WriteLine(" ]");
}
static string ToInfinity(int i) => i == int.MaxValue ? "∞" : i.ToString();
}
}
TypeScript代码
function prim(graph: number[][], numberOfVertexes: number) {
let debug: boolean = true;
let adjVex: number[] = [], // 邻接顶点数组：搜索边的最小权值过程中各边的起点坐标
lowCost = []; // 各边权值数组：搜索边的最小权值过程中各边的权值，数组下标为边的终点。
for (let i = 0; i < numberOfVertexes; i++) // 从图G的下标为0的顶点开始搜索。（也是图G的最小生成树的顶点集合）。
{
adjVex[i] = 0;
}
for (let i = 0; i < numberOfVertexes; i++) // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
{
lowCost[i] = graph[0][i];
}
let k: number = 0; // 初始假定权值最小的边的终点的下标为k。
for (let i = 1; i < numberOfVertexes; i++) {
if (debug) {
console.log(`Loop ${i}`);
console.log(`lowCost: ${printArray(lowCost)}`);
console.log(` adjVex: ${printArray(adjVex)}`);
}
let minimumWeight: number = Number.MAX_VALUE; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (let j = 1; j < numberOfVertexes; j++) {
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
if (!debug) {
console.log(`(${adjVex[k]}, ${k})`);// 输出边
}
adjVex[i] = k; // 此时找到的k值即是权值最小的边的终点。将V[k]放入集合U。（这步可省略，因lowCost[j]已被标为“无需搜索”了）。
lowCost[k] = 0; // 0表示该点已经搜索过了，已不需要再被搜索了。
for (let j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边，去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值；索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时，从k为下标的顶点为起点。
}
}
if (debug) {
console.log(`lowCost: ${printArray(lowCost)}`);
console.log(` adjVex: ${printArray(adjVex)}`);
console.log('');
}
}
}
function primSimplified(graph: number[][], numberOfVertexes: number) {
let adjVex: number[] = [], // 邻接顶点数组：搜索边的最小权值过程中各边的起点坐标
lowCost = []; // 各边权值数组：搜索边的最小权值过程中各边的权值，数组下标为边的终点。
for (let i = 0; i < numberOfVertexes; i++) {
adjVex[i] = 0; // 从图G的下标为0的顶点开始搜索。（也是图G的最小生成树的顶点集合）。
lowCost[i] = graph[0][i]; // 初始从下标为0的顶点开始到下标为i的顶点的边的权值去搜索。找lowCost中权值最小的下标i。
}
let k: number = 0; // 初始假定权值最小的边的终点的下标为k。
for (let i = 1; i < numberOfVertexes; i++) {
let minimumWeight: number = Number.MAX_VALUE; // 搜索过程中发现到的最小的权值。初始设置为最大的整数值以示两点间无边。
for (let j = 1; j < numberOfVertexes; j++) {
if (lowCost[j] != 0 && lowCost[j] < minimumWeight) // lowCost中0表示该点已经搜索过了。lowCost[j] < minimumWeight即发现目前最小权值。
{
minimumWeight = lowCost[j]; // 发现目前最小权值。
k = j; // 目前最小权值的边的终点下标。
}
}
console.log(`(${adjVex[k]}, ${k})`); // 输出边
lowCost[k] = 0; // 0表示该点已经搜索过了，已不需要再被搜索了。
for (let j = 1; j < numberOfVertexes; j++) // 转到以V[k]为开始顶点的边，去与前面u为起始顶点到V[i]为终止顶点的边的权值去比较。
{
if (lowCost[j] != 0 && graph[k][j] < lowCost[j]) // lowCost中0表示该点已经搜索过了。graph[k][j] < lowCost[j]即发现更小权值。
{
lowCost[j] = graph[k][j]; // 更新权值；索引j即终点下标。
adjVex[j] = k; // 下次寻找权值小的边时，从k为下标的顶点为起点。
}
}
}
}
function printArray(array: number[]): string {
let str: string[] = [];
str.push("[ ");
for (let i = 0; i < array.length - 1; i++) // 输出数组的前面n-1个
{
str.push(`${toInfinity(array[i])}, `)
}
if (array.length > 0) // 输出数组的最后1个
{
let n: number = array.length - 1;
str.push(`${toInfinity(array[n])}`);
}
str.push(" ]");
return str.join("");
}
function toInfinity(i: number) {
return i == Number.MAX_VALUE ? "∞" : i.toString();
}
function Main() {
let numberOfVertexes: number = 9,
infinity = Number.MAX_VALUE;
let graph: number[][] = [
[0, 10, infinity, infinity, infinity, 11, infinity, infinity, infinity],
[10, 0, 18, infinity, infinity, infinity, 16, infinity, 12],
[infinity, 18, 0, 22, infinity, infinity, infinity, infinity, 8],
[infinity, infinity, 22, 0, 20, infinity, 24, 16, 21],
[infinity, infinity, infinity, 20, 0, 26, infinity, 7, infinity],
[11, infinity, infinity, infinity, 26, 0, 17, infinity, infinity],
[infinity, 16, infinity, 24, infinity, 17, 0, 19, infinity],
[infinity, infinity, infinity, 16, 7, infinity, 19, 0, infinity],
[infinity, 12, 8, 21, infinity, infinity, infinity, infinity, 0],
];
// let graph: number[][] = [
// [0, 1, 5, infinity, infinity, infinity, infinity, infinity, infinity],
// [1, 0, 3, 7, 5, infinity, infinity, infinity, infinity],
// [5, 3, 0, infinity, 1, 7, infinity, infinity, infinity],
// [infinity, 7, infinity, 0, 2, infinity, 3, infinity, infinity],
// [infinity, 5, 1, 2, 0, 3, 6, 9, infinity],
// [infinity, infinity, 7, infinity, 3, 0, infinity, 5, infinity],
// [infinity, infinity, infinity, 3, 6, infinity, 0, 2, 7],
// [infinity, infinity, infinity, infinity, 9, 5, 2, 0, 4],
// [infinity, infinity, infinity, infinity, infinity, infinity, 7, 4, 0],
// ];
//prim(graph, numberOfVertexes);
primSimplified(graph, numberOfVertexes);
}
Main();
/**
运行结果：
(0, 1)
(1, 2)
(2, 4)
(4, 3)
(4, 5)
(3, 6)
(6, 7)
(7, 8)
*/
参考资料：
《大话数据结构》 - 程杰 著 - 清华大学出版社 第247页
之前不会Markdown语法的角标（Subscript），所以分成了两篇文章。这里将之前的合成整理为一篇。
普里姆（Prim）算法的更多相关文章
- 普里姆Prim算法介绍
普里姆(Prim)算法,和克鲁斯卡尔算法一样,是用来求加权连通图的最小生成树的算法. 基本思想 对于图G而言,V是所有顶点的集合:现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T ...
- 图解最小生成树 - 普里姆(Prim)算法
我们在图的定义中说过,带有权值的图就是网结构.一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边.所谓的最小成本,就是n个顶点,用n-1条边把一个连通图连接 ...
- 普里姆(Prim)算法
/* 普里姆算法的主要思想: 利用二维数组把权值放入,然后找在当前顶点的最小权值,然后走过的路用一个数组来记录 */ # include <stdio.h> typedef char Ve ...
- JS实现最小生成树之普里姆(Prim)算法
最小生成树: 我们把构造连通网的最小代价生成树称为最小生成树.经典的算法有两种,普利姆算法和克鲁斯卡尔算法. 普里姆算法打印最小生成树: 先选择一个点,把该顶点的边加入数组,再按照权值最小的原则选边, ...
- 图的普里姆(Prim)算法求最小生成树
关于图的最小生成树算法------普里姆算法 首先我们先初始化一张图: 设置两个数据结构来分别代表我们需要存储的数据: lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说 ...
- 图的生成树（森林）（克鲁斯卡尔Kruskal算法和普里姆Prim算法）、以及并查集的使用
图的连通性问题:无向图的连通分量和生成树,所有顶点均由边连接在一起,但不存在回路的图. 设图 G=(V, E) 是个连通图,当从图任一顶点出发遍历图G 时,将边集 E(G) 分成两个集合 T(G) 和 ...
- 最小生成树-普利姆(Prim)算法
最小生成树-普利姆(Prim)算法 最小生成树 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一种特殊的图),或者 ...
- 图论---最小生成树----普利姆(Prim)算法
普利姆(Prim)算法 1. 最小生成树(又名:最小权重生成树) 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一 ...
- 经典问题----最小生成树（prim普里姆贪心算法）
题目简述:假如有一个无向连通图,有n个顶点,有许多(带有权值即长度)边,让你用在其中选n-1条边把这n个顶点连起来,不漏掉任何一个点,然后这n-1条边的权值总和最小,就是最小生成树了,注意,不可绕成圈 ...
- 最小生成树之Prim（普里姆）算法
关于什么是Prim(普里姆算法)? 在实际生活中,我们常常碰到类似这种一类问题:如果要在n个城市之间建立通信联络网, 则连通n个城市仅仅须要n-1条线路.这时.我们须要考虑这样一个问题.怎样在最节省经 ...
随机推荐
- 保姆级教程！使用k3d实现K3s高可用！
你是否曾经想尝试使用K3s的高可用模式?但是苦于没有3个"备用节点",或者没有设置相同数量的虚拟机所需的时间?那么k3d这个方案也许你十分需要噢! 如果你对k3d尚不了解,它的名字 ...
- 使用 Android Studio 的日志工具 Log
•Log简介 Android中的日志工具类是Log,这个类中提供了5个方法来供我们打印日志: 1. $Log.v()$ 用于打印那些最为琐碎的,意义最小的日志信息 对应级别 verbose,是 And ...
- 使用Gensim库对文本进行词袋、TF-IDF和n-gram方法向量化处理
Gensim库简介 机器学习算法需要使用向量化后的数据进行预测,对于文本数据来说,因为算法执行的是关于矩形的数学运算,这意味着我们必须将字符串转换为向量.从数学的角度看,向量是具有大小和方向的几何对象 ...
- 【算法学习笔记】组合数与 Lucas 定理
卢卡斯定理是一个与组合数有关的数论定理,在算法竞赛中用于求组合数对某质数的模. 第一部分是博主的个人理解,第二部分为 Pecco 学长的介绍 第一部分 一般情况下,我们计算大组合数取模问题是用递推公式 ...
- canvas判断点是否在路径内
应用场景 我们的项目中有个功能是,canvas上的某个图片选中后可以再这个图片上用鼠标拖拽绘制画笔线条. 当然绘制的边界要控制在图片大小范围内的,那么鼠标是可以随意动的,怎么能控制只在图片上的时候才绘 ...
- 安卓安装kali linux之Termux
解决安装kali无模组问题 https://blog.csdn.net/weixin_44690490/article/details/108599693?utm_source=app 步骤 1.获取 ...
- JDBC_06_处理查询结果集
JDBC处理查询结果集 * ResultSet resultSet=null 结果集对象 * executeQuery(select) 执行SQL查询语句需要的使用executeQuery方法 * i ...
- Day02_15_方法重载
方法重载 1.什么是方法重载? * 方法重载又被称为 OverLoad,是指在同一个类中,具有相同方法名的不同方法,各个方法虽然方法名相同,但是各自的形式参数不同. 2.什么时候考虑使用方法重载? * ...
- .NET6 平台系列2 .NET Framework框架详解
系列目录 [已更新最新开发文章,点击查看详细] 什么是 .NET Framework? .NET Framework 是 Windows 的托管执行环境,可为其运行的应用提供各种服务. 它包括 ...
- OOP-面向对象(一)
一图描述面向对象 类 - 相关参考 定义一个类 # 在定义类名的时候推荐使用大陀峰 class Car: pass # 推荐这么定义 class Car(): pass class Car(objec ...