统计学习：线性可分支持向量机(SVM)

模型

超平面

我们称下面形式的集合为超平面

\[\begin{aligned}
\{ \bm{x} | \bm{a}^{T} \bm{x} - b = 0 \}
\end{aligned} \tag{1}
\]

其中\(\bm{a} \in \mathbb{R}^n\)且\(\bm{a} \ne \bm{0} , \bm{x}\in \mathbb{R}^n, b \in \mathbb{R}\)。解析地看，超平面是关于\(\bm{x}\)的非平凡线性方程的解空间（因此是一个仿射集，仿射集和凸集的概念参考Stephen Boyd的《凸优化》）从几何上看，它的的法向量为\(\bm{a}\)，而常数\(b\in \mathbb{R}\)决定了这个超平面从原点的偏移。这如何得到的呢？这是因为，若我们由法向量\(\bm{a}\)和超平面上一点\(\bm{x}_{0}\)确定超平面，则对超平面上任意一点\(\bm{x}\)，我们可以得到\(\bm{x} - \bm{x}_0\)一定垂直于\(\bm{a}\)，则超平面的集合便可以表示为

\[\begin{aligned}
\{\bm{x} | \bm{a}^{T} (\bm{x} - \bm{x}_0) = 0\}
\end{aligned} \tag{2}
\]

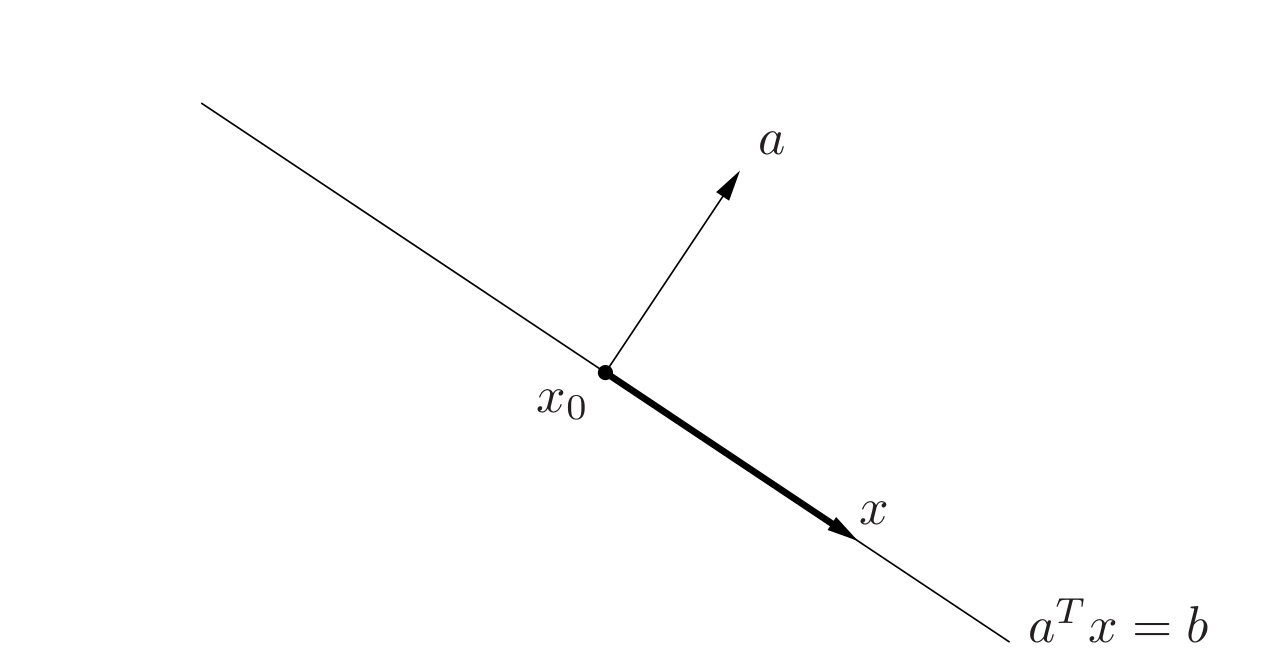
\(\mathbb{R}^2\)中的几何化的解释如下图所示，其中深色箭头表示\(\bm{x} - \bm{x}_0\)：

　

一个超平面将\(\mathbb{R}^n\)划分为两个半空间，（闭的）半空间是具有下列形式的集合：

\[\begin{aligned}
\{\bm{x} | \bm{a}^T \bm{x} -b \leqslant 0\}
\end{aligned} \tag{3}
\]

即（非平凡）的线性不等式的解空间，其中\(a\ne 0\)。半空间是凸的，但不是仿射的。集合\(\{\bm{x} | \bm{a}^T \bm{x} -b < b\}\)是半空间\(\{\bm{x} | \bm{a}^T \bm{x} -b \leqslant 0\}\)的内部，称为开半空间。

线性可分支持向量机

我们定义样本空间为\(\mathcal{X} \subseteq \mathbb{R}^n\)，输出空间为\(\mathcal{Y} = \{+1, -1\}\)。\(\bm{X}\)为输入空间上的随机向量，其取值为\(\bm{x}\)，满足\(\bm{x} \in \mathcal{X}\)；\(Y\)为输出空间上的随机变量，设其取值为\(y\)，满足\(y \in \mathcal{Y}\)。我们将容量为\(m\)的训练样本表示为:

\[\begin{aligned}
D = \{\{\bm{x}^{(1)}, y^{(1)}\}, \{\bm{x}^{(2)}, y^{(2)}\},..., \{\bm{x}^{(m)}, y^{(m)}\}\}
\end{aligned}\tag{4}
\]

当\(y^{(i)} = +1\)时，我们称\(\bm{x}^{(i)}\)为正例；当\(y^{(i)} = -1\)时，称\(\bm{x}^{i}\)为负例。\((\bm{x}^{(i)}, y^{(i)})\)称为样本点。

如果我们假设训练数据集是线性可分的，则我们可以在特征空间中找到一个分离超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0 \}\)，将特征空间划分为\(\{ \bm{x} | \bm{w}^T \bm{x} + b > 0 \}\)和\(\{ \bm{x} | \bm{w}^T \bm{x} + b < 0 \}\)两个开半空间(显然法向量\(\bm{w}\)指

向的一侧为正，另一侧为负)，且为正的一侧对应负类，为负的一侧对应负类。

如果训练集线性可分，则我们存在无穷多个分离超平面将两类样本分开。如果我们采用感知机的误分类最小的训练策略(也就是仅仅保证分类的正确性)，那么我们将求得无穷多个解。我们接下来定义的线性可分支持向量机将利用“间隔最大化”求解最优分离超平面（即能将两组数据正确划分且间隔最大的超平面，我们在“学习策略”板块中将详述这一概念），这时解是唯一的。

<font color='blue'>

形式化地说，给定线性可分的数据集，通过间隔最大化策略学习得到的分离超平面为

\[\begin{aligned}
\{ \bm{x} \| \bm{w}^{*T} \bm{x} + b^{*} = 0 \}
\end{aligned} \tag{5}
\]

以及相应的分类决策函数

\[\begin{aligned}
f(\bm{x}) = \text{sign} (\bm{w}^{*T} \bm{x} + b^{*})
\end{aligned} \tag{6}
\]

称为线性可分支持向量机。

</font>

学习策略

我们前面提到最好的超平面需要能将两组数据正确划分且间隔最大，那么间隔最大如何形式化地定义呢？我们先来看函数间隔和几何间隔的概念。

函数间隔和几何间隔

直观地看，一个点距离超平面的远近可以表示则我们对它进行分类的确信程度。一个点距离超平面越远，则我们对它的分类则越有把握。我们给定超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)和一个实例点\(\bm{x}^{(i)}\)，可以发现\(|\bm{w}^T \bm{x}^{(i)} + b|\)可以相对地表示点\(\bm{x}^{(i)}\)举例超平面的远近，而\(\bm{w}^T \bm{x}^{(i)} + b\)的符号与类标记\(y^{(i)}\)是否一致可以反映分类是否正确。据此，我们用\(y^{(i)} (\bm{w} \cdot \bm{x}^{(i)} + b)\)来对分类的确信度和正确性进行综合表示。\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b)\)为正数，表示分类器能够正确完成分类功能，且\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b)\)越大，则分类器越好；\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b)\)为负数，就表示分类器连正确分类功能都不能完成了，负得越多，表示错的越离谱(HaHa，应该可以这么理解叭)。 于是，我们给出下列函数间隔的定义。

函数间隔 对于给定的数据集\(D\)和超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)，定义该超平面关于数据集中样本点\((\bm{x}^{(i)}, y^{(i)})\)的函数间隔为

\[\begin{aligned}
\hat{\gamma}^{(i)} = y^{(i)}(\bm{w}^T\bm{x}^{(i)} + b)
\end{aligned} \tag{7}
\]

定义该超平面关于训练集\(D\)的函数间隔为该超平面关于\(D\)中所有样本点函数间隔的最小值，即

\[\begin{aligned}
\hat{\gamma} = \underset{i=1,...,m}{\min}\hat{\gamma}^{(i)}
\end{aligned} \tag{8}
\]

如果单单根据函数间隔的大小来选顶最佳超平面，那还不够准确。因为我们知道，令超平面的法向量\(\bm{w}\)经过缩放变换为\(\lambda \bm{w}\)，超平面的截距项缩放变换为\(\lambda b\)，超平面是本身并没有改变的，但函数间隔\(\hat{\gamma}^{(i)}\)却变为\(\lambda \hat{\gamma}^{(i)}\)，这显然与事实不符。因此，我们需要对超平面的法向量加一些约束，如规范化，令\(|| \bm{w} ||=1\)，使得间隔是确定的。这时的函数间隔就是我们后面所提到的几何间隔的一种特殊情况。

我们定义实例\((\bm{x}^{(i)}, y^{(i)})\)到超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)的带符号距离为\(\frac{\bm{w}^T \bm{x}^{(i)} + b}{||\bm{w}||}\)（在法向量那一侧则为正），我们用这个做为来做为分类的确信度。类似地，我们我们用\(y^{(i)} \frac{\bm{w}^T \bm{x}^{(i)} + b}{||\bm{w}||}\)来对分类的确信度和正确性进行综合表示。于是，我们给出下列几何间隔的定义。

几何间隔 对于给定的数据集\(D\)和超平面\(\{ \bm{x} | \bm{w}^T \bm{x} + b = 0\}\)，定义该超平面关于数据集中样本点\((\bm{x}^{(i)}, y^{(i)})\)的几何间隔为

\[\begin{aligned}
\gamma^{(i)} = y^{(i)} \frac{\bm{w}^T \bm{x}^{(i)} + b}{||\bm{w}||}
\end{aligned} \tag{9}
\]

定义该超平面关于训练集\(D\)的函数间隔为该超平面关于\(D\)中所有样本点函数间隔的最小值，即

\[\begin{aligned}
\gamma = \underset{i=1,...,m}{\min}\gamma^{(i)}
\end{aligned} \tag{10}
\]

对比一下式\((7)、(8)\)和式\((9)、(10)\)我们知道，函数间隔和集合间隔存在下列关系\(\gamma^{(i)} = \frac{\hat{\gamma}^{(i)}}{||\bm{w}||}\)，\(\gamma = \frac{\hat{\gamma}}{||\bm{w}||}\)。可以看到，若\(||\bm{w}||=1\)，则函数间隔等于几何间隔，如果\(\bm{w}\)和\(b\)都进行大小为\(\lambda\)的缩放变换，函数间隔也会缩放\(\lambda\)，但几何间隔不变。

间隔最大化

要想使分离超平面更可靠，我们只需要保证该超平面关于\(D\)中所有样本点几何间隔的最小值\(\gamma\)尽量大即可（这样自然就能保证所有点的几何间隔尽量大)，我们称此为间隔最大化策略（或称为硬间隔最大化，和后面训练集近似线性可分的软间隔最大化相对应）。

可以知道，满足间隔最大化的超平面是唯一的，它能够对所有训练数据有足够大的确信度分类，也就是说不仅能够对实例点进行分类，而且对于所有实例点能够有足够大的确信度分类，这样的超平面的未知的测试实例有很好的分类预测能力。我们将该问题表述为以下带约束优化问题：

\[\begin{aligned}
\underset{\bm{w}, b}\max \quad \gamma \\
\text{s.t.} \quad y^{(i)} \frac{\bm{w}^T \bm{x}^{(i)} + b}{||\bm{w}||} \geq \gamma \\
\quad (i = 1, 2, ..., m)
\end{aligned} \tag{11}
\]

根据\(\gamma = \frac{\hat{\gamma}}{||\bm{w}||}\)，我们可以将优化问题\((11)\)写作：

\[\begin{aligned}
\underset{\bm{w}, b}\max \quad \frac{\hat{\gamma}}{||\bm{w}||}\\
\text{s.t.} \quad y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b) \geq \hat{\gamma} \\
\quad (i = 1, 2, ..., m)
\end{aligned} \tag{12}
\]

我们将\(\bm{w}\)和\(b\)缩放变换为\(\lambda \bm{w}\)和\(\lambda b\)，则函数间隔\(\hat{\gamma}\)变为\(\lambda \hat{\gamma}\)。我们法线函数间隔的这一改变对\((11)\)中最优化问题的约束目标函数和不等式约束都没有影响,也就是说它产生了一个等价的最优化问题。

这样，就可以取\(\hat{\gamma}=1\)。将\(\hat{\gamma}=1\)代入上面的最优化问题，相当于最大化\(\frac{1}{||\bm{w}||}\)。不过这样目标函数非凸，一般较难求解，为了将其转换为凸优化问题，我们将原本的优化目标函数等价转换为最小化\(\frac{1}{2}||\bm{w}||^2\)，这样我们就将线性可分支持向量机的学习策略转换为了一个(凸)二次规划问题:

\[\begin{aligned}
\underset{\bm{w}, b}\max \quad \frac{1}{2} || \bm{w}||^2\\
\text{s.t.} \quad y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b) -1 \geq 0 \\
\quad (i = 1, 2, ..., m)
\end{aligned} \tag{13}
\]

该形式称为线性可分支持向量机的标准型。

---

附： 这里提一下凸优化问题和二次规划问题的概念。凸优化问题定义如下

\[\begin{aligned}
\underset{\bm{x}}\min \quad f_0(\bm{x})\\
\text{s.t.} \quad f_i(\bm{x}) \leq 0 \quad (i = 1, 2, ..., m) \\
h_i(\bm{x}) = 0 \quad (i = 1, 2, ..., p)
\end{aligned} \tag{14}
\]

其中目标函数\(f_0(\bm{x})\)和约束函数\(f_i(\bm{x})\)都为凸函数，且等式约束函数\(h_i(\bm{x})\)为仿射函数(也就是说，\(h_i(\bm{x})\)可以写成\(h_i(\bm{x})= \bm{a}^T\bm{x} + b\)的形式。

特别地，当凸优化问题的目标函数\(f_0(\bm{x})\)是（凸）二次型并且约束函数\(f_i(\bm{x})\)为仿射时，该问题称为二次规划(QP)。二次规划可以表述为：

\[\begin{aligned}
\underset{\bm{x}}\min \quad (\frac{1}{2})\bm{x}^T\textbf{P}\bm{x} + \textbf{q}^{T} \bm{x} + r \\
\text{s.t.} \quad f_i(\bm{x}) \leq 0 \quad (i = 1, 2, ..., m) \\
h_i(\bm{x}) = 0 \quad (i = 1, 2, ..., p)
\end{aligned} \tag{15}
\]

其中\(\textbf{P}\)是对称正定矩阵(在式\((13)\)中，\(\textbf{P}\)即是单位阵\(\textbf{I}\))，约束函数\(f_i(\bm{x})\)和等式约束函数\(h_i(\bm{x})\)都是仿射函数。

---

接下来我们会介绍该凸二次规划问题的求解算法。

算法

接下来我们推导求解线性可分支持向量机的高效算法。（真的是万般皆推导，难的是算法的推导过程，算法实现反而很简单）

直接求解式\((13)\)计算复杂度过高，而凸优化理论中告诉了我们许多可以高效求解\((13)\)问题的理论。我们将问题\((13)\)的形式做为原始问题(primal problem)。应用拉格朗日对偶性。通过求解对偶问题(dual problem)同样得到原始问题的最优解，而且求解会更加高效。问题求解可分两步走。

1. 推导原始问题的对偶形式并求得对偶问题的最优解\(\alpha^{*}\)。

我们引入拉格朗日乘子向量\(\bm{\alpha} = ( \alpha_{1}, \alpha_{2},..., \alpha_{m} )^T\)，每个不等式约束对应一个拉格朗日乘子\(\alpha_i \geq 0, i=1,2,...,m\)，我们以此定义拉格朗日函数：

\[\begin{aligned}
L(\bm{w}, b, \bm{\alpha}) = \frac{1}{2}||\bm{w}||^2 + (- \sum_{i=1}^{m}\alpha_i y^{(i)}(\bm{w}^T\bm{x}^{(i)}+b)) + \sum_{i=1}^{m}\alpha_i
\end{aligned} \tag{16}
\]

（注意，标准凸优化问题式\((14)\)的约束项是小于等于，我们的式\((13)\)是大于等于，在写出拉格朗日函数前，需要对原来的约束不等式两边同乘\(-1\)）

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题：

\[\begin{aligned}
\underset{\bm{\alpha}}{\max}\underset{\bm{w}, b}{\min}L(\bm{w}, b, \bm{\alpha})
\end{aligned} \tag{17}
\]

我们将问题拆解为先对\(\bm{w}\)、\(b\)求极小，再求对\(\bm{\alpha}\)求极大。

(1) 首先，我们求\(g(\bm{\alpha}) = \underset{\bm{w},b}{\min}L(\bm{w}, b, \bm{\alpha})\)。由凸函数\(L(\bm{w}, b, \bm{\alpha})\)极值满足的一阶必要条件有

\[\begin{aligned}
\nabla_{\bm{w}}L(\bm{w}, b, \bm{\alpha}) = \bm{w} - \sum_{i=1}^{m}\alpha_i y^{(i)}\bm{x}^{(i)} = 0 \\
\nabla_{b}L(\bm{w}, b, \bm{\alpha}) = - \sum_{i=1}^{m}\alpha_iy^{(i)} = 0
\end{aligned} \tag{18}
\]

可得：

\[\begin{aligned}
\bm{w} = \sum_{i=1}^{m}\alpha_i y^{(i)}\bm{x}^{(i)}\\
\sum_{i=1}^{m}\alpha_iy^{(i)} = 0
\end{aligned} \tag{19}
\]

关于\(\bm{w}\)的等式是一个对\(\bm{w}\)的显式替换，而第二个等式是对式\(L(\bm{w}, b, \alpha)\)的一个约束，我们先将式\((19)\)中的等式一代入式\((16)\)的\(L(\bm{w}, b, \bm{\alpha})\)中有

\[L(\bm{w}, b, \bm{\alpha}) =\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy^{(i)}y^{(j)}\langle \bm{x}^{(i)}, \bm{x}^{(j)}\rangle - \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy^{(i)}y^{(j)}\langle \bm{x}^{(i)}, \bm{x}^{(j)}\rangle - \sum_{i=1}^{m}\alpha_iy^{(i)}b + \sum_{i=1}^{m}\alpha_i
\tag{20}
\]

虽然式\((19)\)没有显式的关于\(b\)的等式可供代入，但我们发现将第二个等式\(\sum_{i=1}^{m}\alpha_iy^{(i)}=0\)带入后就可以将\(b\)的那项消掉，得到原问题的拉格朗日对偶函数(或对偶函数)为

\[g(\bm{\alpha}) = \underset{\bm{w}, b}{\min}L(\bm{w}, b, \bm{\alpha}) = -\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy^{(i)}y^{(j)}\langle \bm{x}^{(i)}, \bm{x}^{(j)}\rangle + \sum_{i=1}^{m}\alpha_i
\]

(2) 接下来我们再求\(\underset{\bm{\alpha}}{\max}{g(\bm{\alpha})}\)，这也就是我们需要求的对偶问题。

\[\begin{aligned}
\underset{\bm{\alpha}}{\max} -\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy^{(i)}y^{(j)}\langle \bm{x}^{(i)}, \bm{x}^{(j)}\rangle + \sum_{i=1}^{m}\alpha_i \\
s.t. \sum_{i=1}^{m}\alpha_iy^{(i)} = 0 \\
\alpha_i \geq 0, i, 2,...,m
\end{aligned}
\tag{22}
\]

可以看出，式\((22)\)这个对偶问题只用求解\(\bm{\alpha}\)系数而\(\bm{\alpha}\)系数只有支持向量才非0，其他全为0，这样的话求解对偶问题的计算就会更加高效。至于求解式\((22)\)算法的具体实现(一般采用内点法)可以调用凸优化库Gurobi，在此不再详述。

解式\((22)\)后我们得到\(\bm{\alpha}\)的解\(\bm{\alpha}^{*} = (\alpha_1^{*}, \alpha_2^{*}, ..., \alpha_m^{*})^{T}\)。

2. 由对偶问题的最优解\(\alpha^{*}\)求得原始问题式\((13)\)的最优解\(\bm{w}^{*},b^{*}\)

如果\(\alpha^{*} = (\alpha_1^{*}, \alpha_2^{*}, ..., \alpha_{m}^{*})^{T}\)是对偶最优化问题的解，我们将\(\alpha_i>0\)对应的实例点集合被称为支持向量，我们设\(U = \{\alpha_i | \alpha_i >0 \}\)，我们\(U\)从中随机采一个\(\alpha_s\)，对应的样本为\((\bm{x}^{(s)}, y^{(s)})\)，可按下式求得原始最优化问题\((13)\)的解\(\bm{w}^{*}, b^*\)。

\[\begin{aligned}
\bm{w}^{*} = \sum_{i=1}^{m}\alpha_i^{*}y^{(i)}\bm{x}^{(i)} \\
b^{*} = y^{(s)} - \sum_{i=1}^{m}\alpha_i^*y^{(i)}\langle \bm{x}^{(s)}, \bm{x}^{(i)} \rangle
\end{aligned}
\tag{23}
\]

附： 式\((23)\)可根据KKT条件推导而得。KKT条件如下：

\[\nabla_{\bm{w}}L(\bm{w}^{*}, b^{*}, \bm{\alpha}^{*}) = \bm{w}^{*} - \sum_{i=1}^{m}\alpha_{i}y^{(i)}\bm{x}^{(i)} = 0 \\
\nabla_{b}L(\bm{w}^{*}, b^{*}, \bm{\alpha}^{*}) = - \sum_{i=1}^{m}\alpha_iy^{(i)} = 0 \\
\alpha_{i}^{*}[y^{(i)}(\bm{w^{*}}^T \bm{x}^{(i)}+b^{*}) - 1] = 0, \quad i=1,2,...,m \\
y^{(i)}(\bm{w^{*}}^T \bm{x}^{(i)}+b^{*}) - 1 \geq 0, \quad i=1, 2,..., m \\
a_i^* \geq 0
\tag{24}
\]

由式\((24)\)中第一个等式，我们可得：

\[\bm{w}^* = \sum_{i=1}^{m}\alpha_{i}y^{(i)}\bm{x}^{(i)}
\tag{25}
\]

其中至少有一个\(\alpha_i^{*}>0\)(用反证法，假设\(\alpha_i\)全为0，则\(\bm{w}^{*}\)为0，而易得\(\bm{w}\)为0不是原始问题\((13)\)的最优解，产生矛盾，故假设不符)。

式\((24)\)中第三个等式称为KKT互补条件，我们设\(U = \{\alpha_i^* | \alpha_i^* >0 \}\)，我们\(U\)从中随机采一个\(\alpha_s^*\)，对应的样本为\((\bm{x}^{(s)}, y^{(s)})\)。因为有\(\alpha_s^*>0\)，则必有

\[y^{(s)}(\bm{w^{*}}^T \bm{x}^{(s)}+b^{*}) - 1 = 0
\tag{26}
\]

我们将式\((25)\)代入式\((26)\)，方程两边同乘\(y^{(s)}\)，并注意到\(y^{(s)2}=1\)，我们有

\[b^{*} = y^{(s)} - \sum_{i=1}^{m}\alpha_i^{*}y^{(i)}\langle \bm{x}^{(i)}, \bm{x}^{(s)} \rangle
\tag{27}
\]

---

这样，我们就可以得到分离超平面如下：

\[\{\bm{x} | \sum_{i=1}^{m}\alpha_i^*y^{(i)}\langle \bm{x}^{(i)}, \bm{x} \rangle + b^* = 0\}
\tag{29}
\]

分类决策函数如下:

\[f(\bm{x}) = \text{sign}(\sum_{i=1}^{m}\alpha_i^*y^{(i)}\langle \bm{x}^{(i)}, \bm{x} \rangle + b^*)
\tag{29}
\]

(之所以写成\(\langle \bm{x}^{(i)}, \bm{x} \rangle\)的内积形式是为了方便我们后面引入核函数)

给定测试样本\(\bm{x}^*\)，我们就能按照式\((29)\)计算其类别\(f(\bm{x}^*)\)。由式\((23)\)可知，\(\bm{w}^*\)和\(b^*\)只依赖于\(\alpha_i>0\)的样本点\((\bm{x}^{(i)}, y^{(i)})\)，而其他样本点对\(\bm{w}^*\)和\(b\)没有影响。我们将训练数据中对应于\(a_i^*>0\)的实例点\(\bm{x}^{(i)} \in \mathbb{R}^n\)称为支持向量。

综上，按照式\((13)\)的策略求解线性可分支持向量机的算法如下：　

　

观察算法的2、３步可知，我们只需要关注\(\alpha_i>0\)对应的相关的实例(也就是支持向量)，故实际计算复杂度其实很低。