hdu1232 并查集总结

前言

在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。

这一类问题其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。

定义

并查集（Disjoint Set），即“不相交集合”，是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。集就是让每个元素构成一个单元素的集合，也就是按一定顺序将属于同一组的元素所在的集合合并。

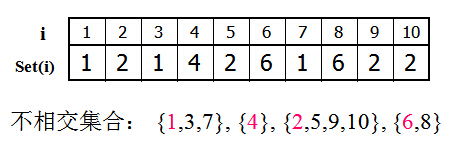
将编号分别为1…N的N个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在集合。

常见两种操作：

• 合并两个集合
• 查找某元素属于哪个集合

用编号最小的元素标记所在集合；定义一个数组set[1...n]，其中set[i]表示元素i 所在的集合；

算法实现

查找

时间复杂度：\(O(1)\)

find1(x)
{
    return set[x];
}

合并

时间复杂度：\(O(n)\)

Merge1(a,b)
{
    i = min(a,b);
    j = max(a,b);
    for (k = 1; k <= N; k++) {
        if (set[k] == j)
            set[k] = i;
    }
}

对于合并操作，必须搜索全部元素！有没有可以改进的地方呢？

算法的优化

使用树结构

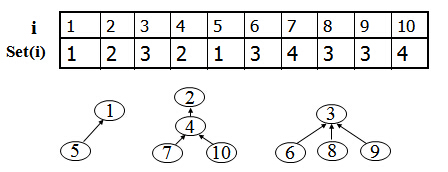
每个集合用一棵“有根树”表示，定义数组set[1...n]

• set[i] = i，则 i 表示本集合，并且是集合所对应树的根
• set[i] = j，j<>i，则 j 是 i 的父节点
  
  

查找

时间复杂度（最坏）：\(O(n)\)

find2(x)
{
   r = x;
   while (set[r] != r)
      r = set[r];
   return r;
}

合并

时间复杂度：\(O(1)\)

merge2(a, b)
{
    if (a<b)
       set[b] = a;
    else
       set[a] = b;
}

避免最坏情况

方法：将深度小的树合并到深度大的树

实现：假设两棵树的深度分别为h1和h2, 合并后的树的高度为h，则

\[h =
\begin{cases}
max(h1, h2), & \text{if h1<>h2} \\
h1+1, & \text{if h1=h2}
\end{cases}
\]

效果：任意顺序的合并操作以后，包含k个节点的树的最大高度不超过\(\log_2{k}\)

查找

时间复杂度：\(O(\log_2{n})\)

find2(x)
{
   r = x;
   while (set[r] != r)
      r = set[r];
   return r;
}

合并

时间复杂度：\(O(1)\)

merge3(a,b)
{
    if (height(a) == height(b)) {
       height(a) = height(a) + 1;
       set[b] = a;
    } else if (height(a) < height(b)) {
       set[a] = b;
    } else {
       set[b] = a;
    }
}

路径压缩

思想：每次查找的时候，如果路径较长，则修改信息，以便下次查找的时候速度更快。

步骤:

1. 找到根结点
2. 修改查找路径上的所有节点，将它们都指向根结点

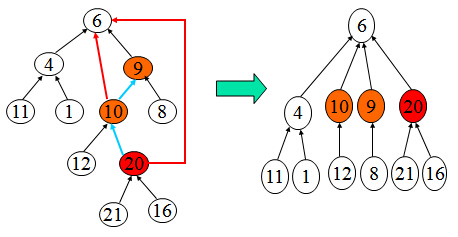
路径压缩示意图:

查找

find3(x)
{
      r = x;
      while (set[r] != r) //循环结束，则找到根节点
          r = set[r];
      i = x;
      while (i != r) //本循环修改查找路径中所有节点
      {
          j = set[i];
          set[i] = r;
          i = j;
      }
}

hdu1232

#include<stdio.h>
int x[1005];
int min(int a,int b);
int max(int a,int b);
void xs(int a,int b);
int fine(int a);
int main()
{
    int n,m,i,a,b;
    while(scanf("%d",&n)&&n)
    {
        int sum = -1;
        scanf("%d",&m);
        for(i=1;i<=n;i++) x[i]=i;   //首先把各自的父节点设为自身
        for(i=1;i<=m;i++)
        {
            scanf("%d%d",&a,&b);
            xs(a,b);  //合并两个集合
        }
        for(i=1;i<=n;i++)
        {
            if(x[i]==i) sum++;    //算出（最后不同集合的个数-1）即为所求
        }
        printf("%d\n",sum);
    }
    return 0;
}
int min(int a,int b)
{
    return a<b ? a : b;
}
int max(int a,int b)
{
    return a>b ? a : b;
}
int fine(int a)
{
    if(x[a]==a) return a;
    else return fine(x[a]);
}
void xs(int a,int b)
{
    x[max(fine(a),fine(b))] = min(fine(a),fine(b));
}