PriorityQueue的用法和底层实现原理

定义

PriorityQueue类在Java1.5中引入并作为 Java Collections Framework 的一部分。PriorityQueue是基于优先堆的一个无界队列，这个优先队列中的元素可以默认自然排序或者通过提供的Comparator（比较器）在队列实例化的时排序。

优先队列不允许空值，而且不支持non-comparable（不可比较）的对象，比如用户自定义的类。优先队列要求使用Java Comparable和Comparator接口给对象排序，并且在排序时会按照优先级处理其中的元素。

PriorityQueue是非线程安全的，所以Java提供了PriorityBlockingQueue（实现BlockingQueue接口）用于Java多线程环境。

案例代码

• 小根堆

/**
     * @Description: 小根堆
     * @Author:
     * @Date:  2021-12-08
     * @Param:
     * @return:
     **/
    public void smallHeap(){
        PriorityQueue<Integer> priorityQueue=new PriorityQueue();
        priorityQueue.add(1);
        priorityQueue.add(2);
        priorityQueue.add(9);
        priorityQueue.add(4);
        priorityQueue.add(8);
        priorityQueue.add(0);
        while (!priorityQueue.isEmpty()){
            System.out.println(priorityQueue.poll());
        }
    }

//输出
0
1
2
4
8
9

• 大根堆

/**
     * @Description: 大根堆
     * @Author:
     * @Date:  2021-12-08
     * @Param:
     * @return:
     **/
    public void bigHeap(){
        PriorityQueue<Integer> priorityQueue=new PriorityQueue(new MyComparator());
        priorityQueue.add(13);
        priorityQueue.add(2);
        priorityQueue.add(9);
        priorityQueue.add(663);
        priorityQueue.add(8);
        priorityQueue.add(0);
        while (!priorityQueue.isEmpty()){
            System.out.println(priorityQueue.poll());
        }
    }
/**
     * @Description: 自定义比较器 实现大根堆
     * @Author: zhuyang
     * @Date:  2021-12-08
     * @Param:
     * @return:
     **/
    public static class MyComparator implements Comparator<Integer>{

        @Override
        public int compare(Integer o1, Integer o2) {
            return o2-o1;
        }
    }
//输出
663
13
9
8
2
0

图列

• 小根堆
  
  

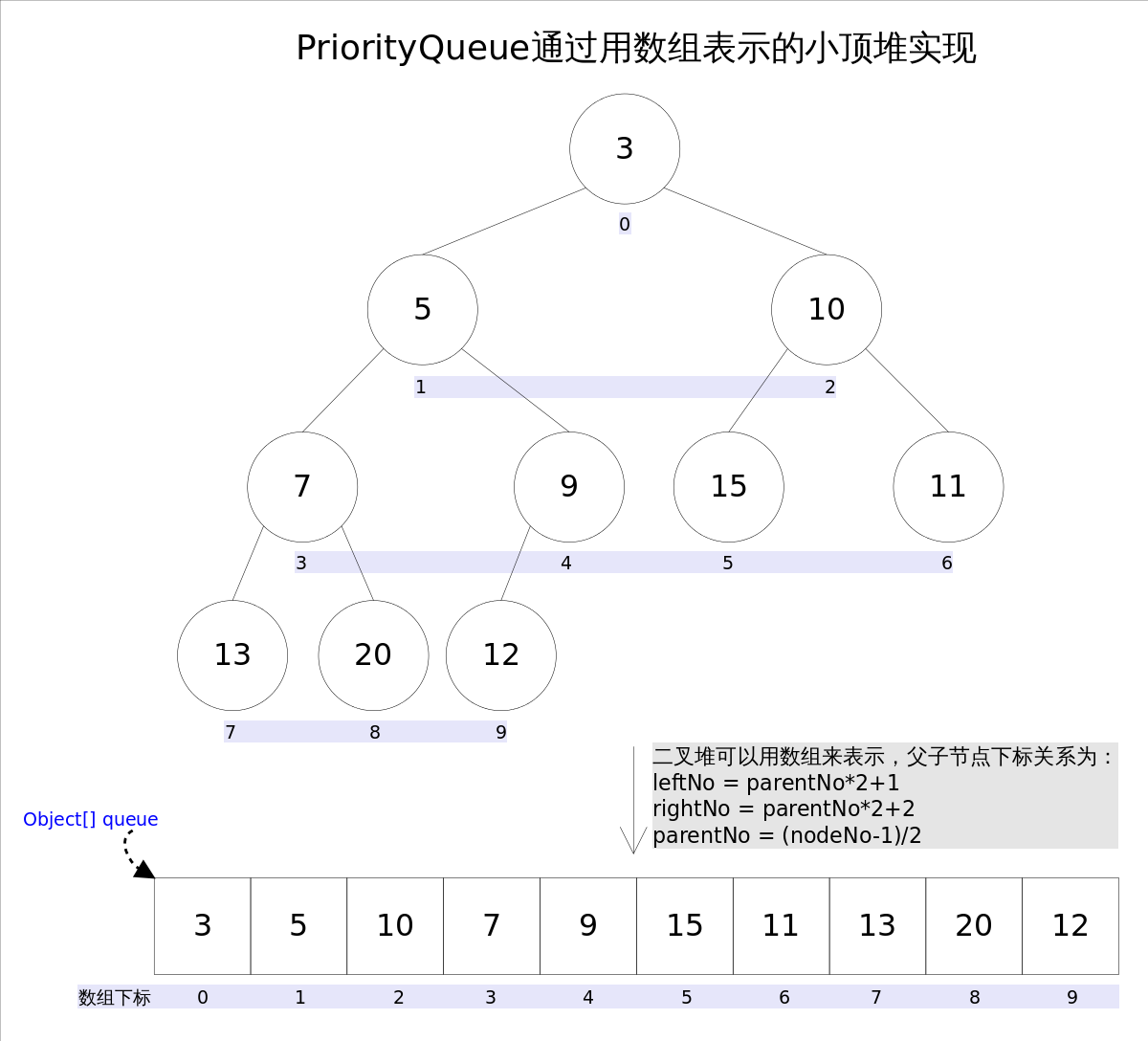
堆顶元素一定为该完全二叉树所有节点最小元素;任意一个非叶子节点的权值，都不大于其左右子节点的权值。

• 大根堆
  
  

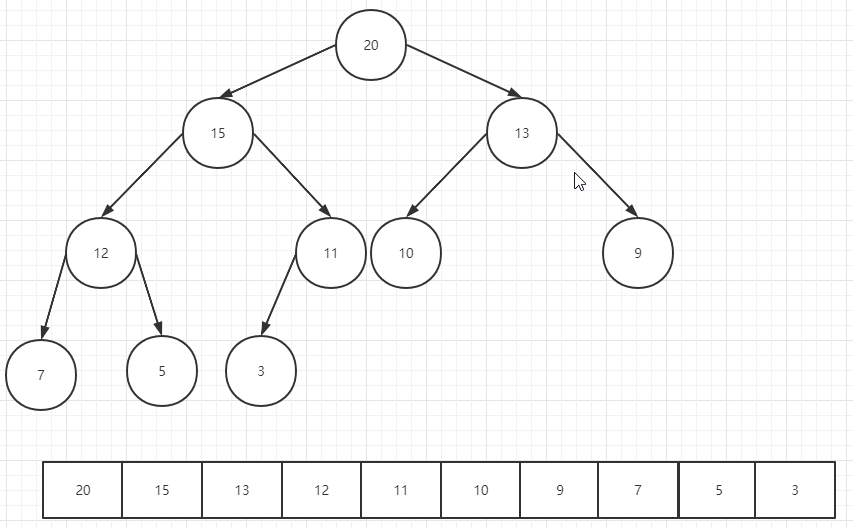
堆顶元素一定为该完全二叉树所有节点最大元素;任意一个非叶子节点的权值，都不小于其左右子节点的权值。

底层原理

• add()和offer()
  
  add(E e)和offer(E e)的语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则则会返回false。对于PriorityQueue这两个方法其实没什么差别。
  
  
  
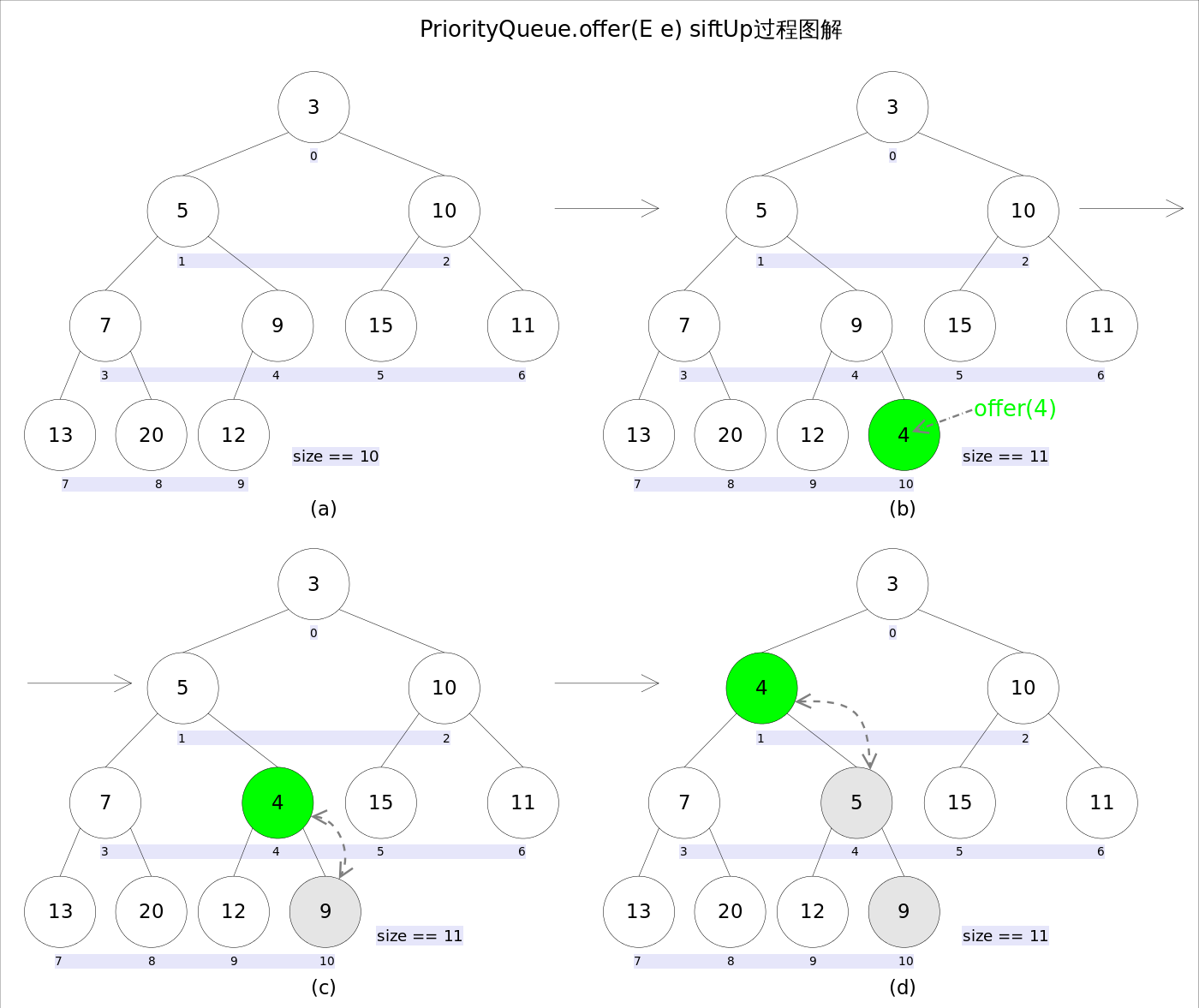
  新加入的元素可能会破坏小顶堆的性质，因此需要进行必要的调整。

//offer(E e)
public boolean offer(E e) {
    if (e == null)//不允许放入null元素
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1);//自动扩容
    size = i + 1;
    if (i == 0)//队列原来为空，这是插入的第一个元素
        queue[0] = e;
    else
        siftUp(i, e);//调整
    return true;

}

上述代码中，扩容函数grow()类似于ArrayList里的grow()函数，就是再申请一个更大的数组，并将原数组的元素复制过去，这里不再赘述。需要注意的是siftUp(int k, E x)方法，该方法用于插入元素x并维持堆的特性。

//siftUp()
private void siftUp(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;//parentNo = (nodeNo-1)/2
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)//调用比较器的比较方法
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

新加入的元素x可能会破坏小顶堆的性质，因此需要进行调整。调整的过程为：从k指定的位置开始，将x逐层与当前点的parent进行比较并交换，直到满足x >= queue[parent]为止。注意这里的比较可以是元素的自然顺序，也可以是依靠比较器的顺序。

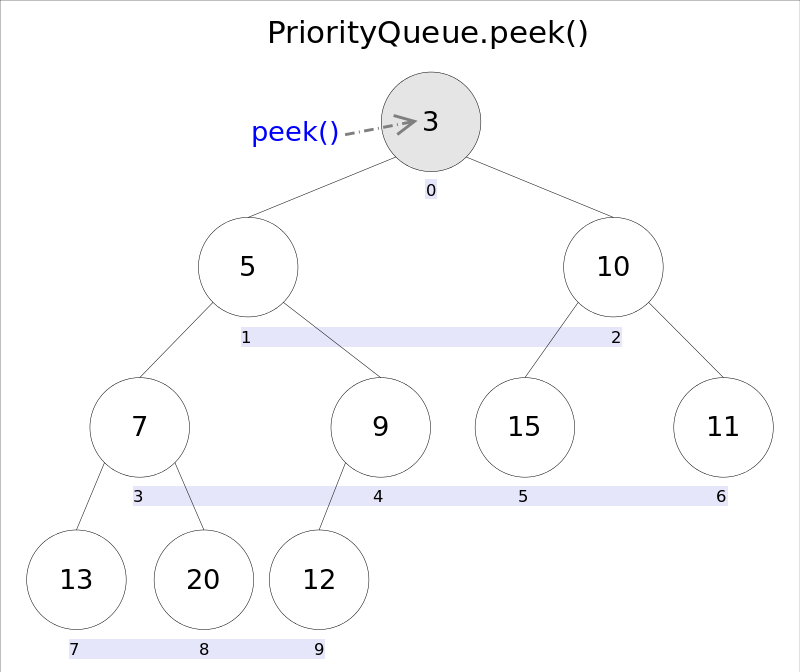
• element()和peek()
  
  element()和peek()的语义完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素，二者唯一的区别是当方法失败时前者抛出异常，后者返回null。根据小顶堆的性质，堆顶那个元素就是全局最小的那个；由于堆用数组表示，根据下标关系，0下标处的那个元素既是堆顶元素。所以直接返回数组0下标处的那个元素即可。
  
  

//peek()
public E peek() {
    if (size == 0)
        return null;
    return (E) queue[0];//0下标处的那个元素就是最小的那个
}

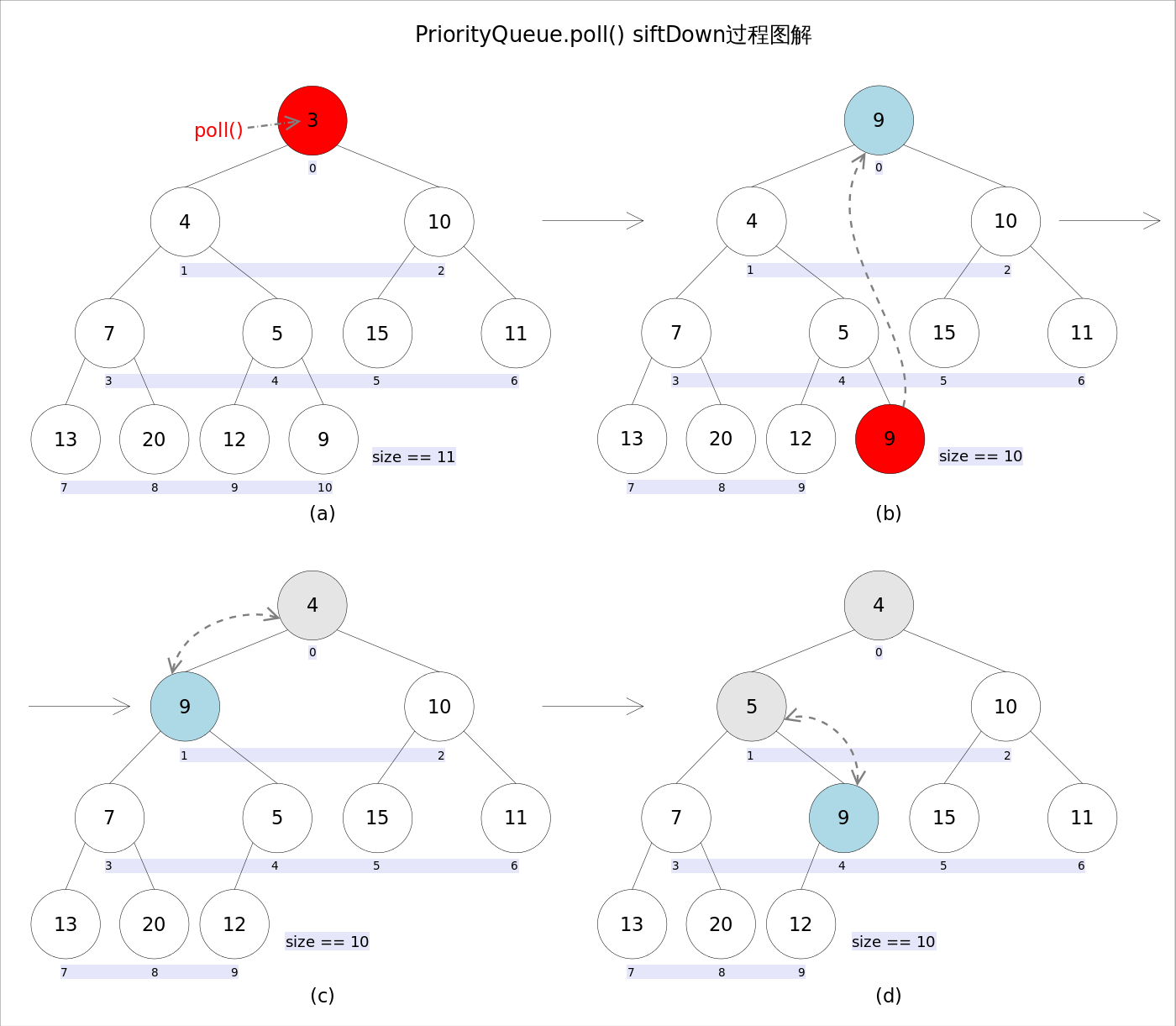
• remove()和poll()
  
  remove()和poll()方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。
  
  

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];//0下标处的那个元素就是最小的那个
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x);//调整
    return result;
}

上述代码首先记录0下标处的元素，并用最后一个元素替换0下标位置的元素，之后调用siftDown()方法对堆进行调整，最后返回原来0下标处的那个元素（也就是最小的那个元素）。重点是siftDown(int k, E x)方法，该方法的作用是从k指定的位置开始，将x逐层向下与当前点的左右孩子中较小的那个交换，直到x小于或等于左右孩子中的任何一个为止。

//siftDown()
private void siftDown(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        //首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标
        int child = (k << 1) + 1;//leftNo = parentNo*2+1
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c;//然后用c取代原来的值
        k = child;
    }
    queue[k] = x;
}

转载

https://blog.csdn.net/u010623927/article/details/87179364

Gitte地址

https://gitee.com/zhuayng/foundation-study/tree/develop/JavaBasis/AlgorithmaBasic2020/src/main/java/com/cdyx/algorithmabasic2020/class06