【Python机器学习实战】聚类算法（1）—

实战部分主要针对某一具体算法对其原理进行较为详细的介绍，然后进行简单地实现（可能对算法性能考虑欠缺），这一部分主要介绍一些常见的一些聚类算法。

K-means聚类算法

0.聚类算法算法简介

　　聚类算法算是机器学习中最为常见的一类算法，在无监督学习中，可以说聚类算法有着举足轻重的地位。

　　提到无监督学习，不同于前面介绍的有监督学习，无监督学习的数据没有对应的数据标签，我们只能从输入X中去进行一些知识发现或者预处理。

　　过去在有监督学习中，我们（让机器）通过X去预测Y，而到了无监督学习中，我们（让机器）只能从X去发现什么，或者X中哪些输入对我们是有用的，因此：

　　无监督学习中包括了两大方面：聚类和降维。

　　在无监督学习中，我们通过X可以发现什么。聚类就是主要回答这一类问题。而对于一个具有很多维的数据，那些维度对于我们想要知道的事情的影响比较大，这就是降维要做的事情。

　　聚类算法，顾名思义，就是一种能将属于同类别的数据聚集在一起的算法，称之为“物以类聚”。聚类的目的就是将相似的对象归为同一簇中，不相似的对象归到不同簇中。

　　聚类算法比较常用的有K-means、层次聚类算法、DBSCAN等，这些后面会一一介绍，本节主要是K-means算法。

　　具体聚类算法有很多应用场景，如客户群体分析、社交网络分析等，还有很多间接的应用，如数据预处理、半监督学习等。

1.K-means聚类原理

　　K-means聚类就是给定一组数据，以及一个k值，然后把这些数据分为k个类别的算法。其中k是事先需要给定的参数。每一个簇（类别）通过这个簇的中心（质心）进行描述。大概就是下面这样子：

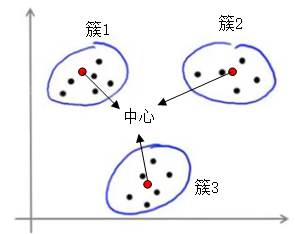
　　K-means算法是聚类算法中较为简单的一种，原理简单，易于实现。其原理大致是：首先给定k个中心（质心），然后将数据分别划分到k个簇中去，也就是说把每个数据分到距离其最近的那个中心所在的簇中。

　　然后重新计算每个簇的中心，即属于这个簇的样本的均值即为新的簇的中心。

　　具体算法流程如下：

　　　　1.初始化k个点作为聚类中心（通常随机选择）

　　　　2.计算每个样本距离k个聚类中心的距离，然后将每个样本分到距离其最近的中心所属的簇中；

　　　　3.重新计算k个簇的中心，中心为簇中所包含数据点的均值，；

　　　　4.重复2~3，知道k个聚类中心不再移动。

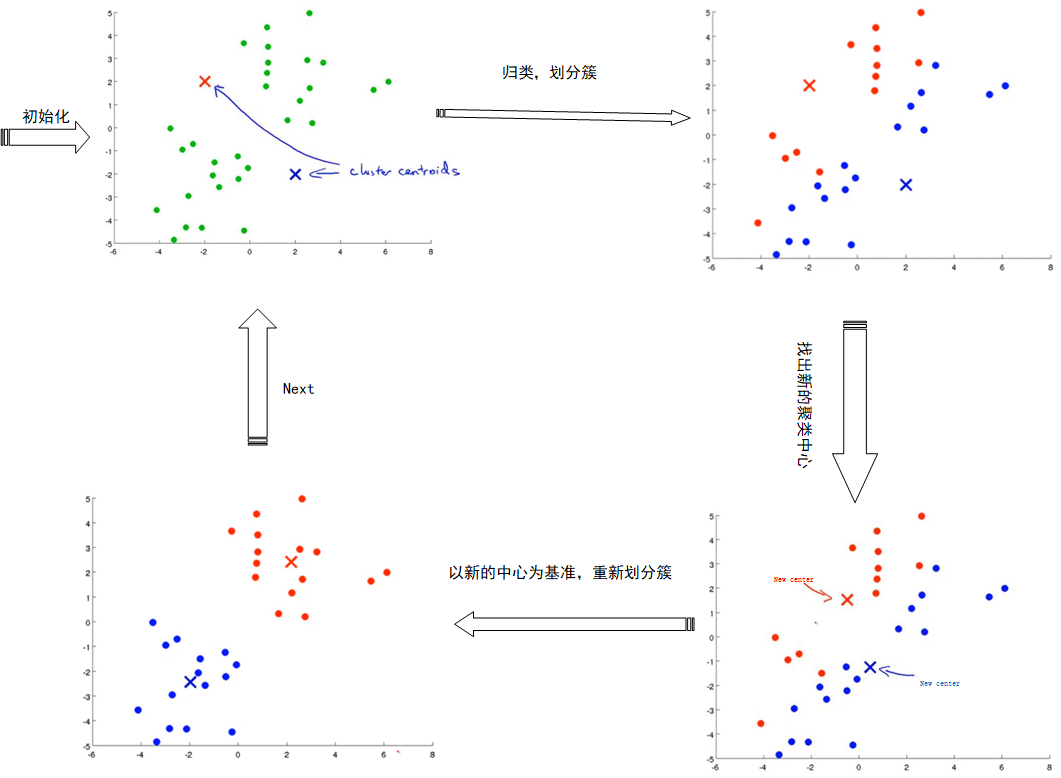
　　图片来源于网络，这里稍微整理了一下。

　上面就是K-means算法的过程，下面我们先对上面的过程做一个简单的实现：

from numpy import *

# 定义距离计算

def cal_dist(vect_a, vect_b):

    return sqrt(sum(power(vect_a, vect_b, 2)))

# 随机选取聚类中心

def rand_center(data, k):

    n = shape(data)[1]

    centroids = mat(zeros((k, n)))

    for j in range(n):

        min_j = min(data[:, j])

        range_j = float(max(data[:, j]) - min(data[:, j]))

        # np.random.rand(k, 1) 生成size为（k,1）的0~1的随机array

        centroids[:, j] = min_j + range_j * random.rand(k, 1)

    return centroids

def Kmeans(data, k, dis_meas=cal_dist, create_center=rand_center):

    m = shape(data)[0]

    # 用于保存每个样本所属类别的矩阵，第0维为所属类别，第一维为样本距离该类别的距离

    clusterAssment = mat(zeros((m, 2)))

    # 初始化聚类中心

    centroids = create_center(data, k)

    cluster_changed = True

    while cluster_changed:

        cluster_changed = False

        for i in range(m):

            min_dist = inf

            min_index = -1

            for j in range(k):

                dist_ij = dis_meas(data[i, :], centroids[j, :])

                if dist_ij < min_dist:

                    min_dist = dist_ij

                    min_index = j

            # 如果样本的类别发生了变化，则继续迭代

            if clusterAssment[i, 0] != min_index:

                cluster_changed = True

            # 第i个样本距离最近的中心j存入

            clusterAssment[i, :] = min_index, min_dist ** 2

        print(centroids)

        # 重新计算聚类中心

        for cent in range(k):

            # 找出数据集中属于第k类的样本的所有数据，nonzero返回索引值

            points_in_cluster = data[nonzero(clusterAssment[:, 0].A == cent)[0]]

            centroids[cent, :] = mean(points_in_cluster, axis=0)

    return centroids, clusterAssment

　　然后定义一个读取数据的函数，使用testdata进行测试：

def loadData(filename):

    data_mat = []

    fr = open(filename)

    for line in fr.readlines():

        cur_line = line.strip().split('\t')

        flt_line = [float(example) for example in cur_line]

        data_mat.append(flt_line)

    return mat(data_mat)

data = loadData('.\testSet.txt')

centroids, cluster_ass = Kmeans(data, 4, dis_meas=cal_dist, create_center=rand_center)

import matplotlib.pyplot as plt

data_0 = data[nonzero(cluster_ass[:, 0].A == 0)[0]]

data_1 = data[nonzero(cluster_ass[:, 0].A == 1)[0]]

data_2 = data[nonzero(cluster_ass[:, 0].A == 2)[0]]

data_3 = data[nonzero(cluster_ass[:, 0].A == 3)[0]]

plt.scatter(data_0[:, 0].A[:, 0], data_0[:, 1].A[:, 0])

plt.plot(centroids[0, 0], centroids[0, 1], '*', markersize=20)

plt.scatter(data_1[:, 0].A[:, 0], data_1[:, 1].A[:, 0])

plt.plot(centroids[1, 0], centroids[1, 1], '*', markersize=20)

plt.scatter(data_2[:, 0].A[:, 0], data_2[:, 1].A[:, 0])

plt.plot(centroids[2, 0], centroids[2, 1], '*', markersize=20)

plt.scatter(data_3[:, 0].A[:, 0], data_3[:, 1].A[:, 0])

plt.plot(centroids[3, 0], centroids[3, 1], '*', markersize=20)

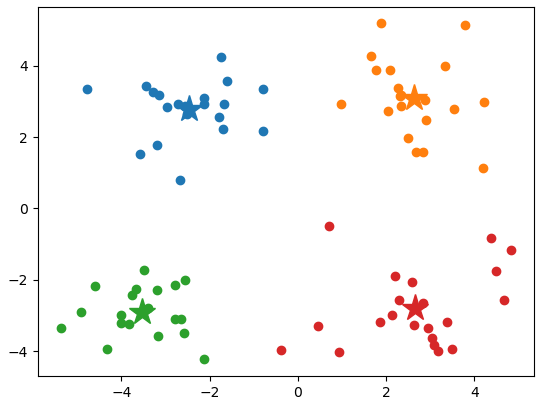
2.关于K-means算法的问题和改进

　　K-means的损失函数为数据点与数据点所在的聚类中心之间的距离的平方和，也就是：

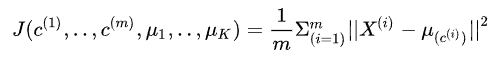
　　其中μ为数据点所在的类别的聚类中心，我们期望最小化损失，从而找到最佳的聚类中心和数据所属的类别。

2.1 陷入局部最小值问题及改进

　　然而，上面说到，在K-means算法的第一步是随机选取k个位置作为聚类中心，这可能就会导致，不同的初始位置，对最终的聚类结果有着很大的影响，比如当把k设置为2时：

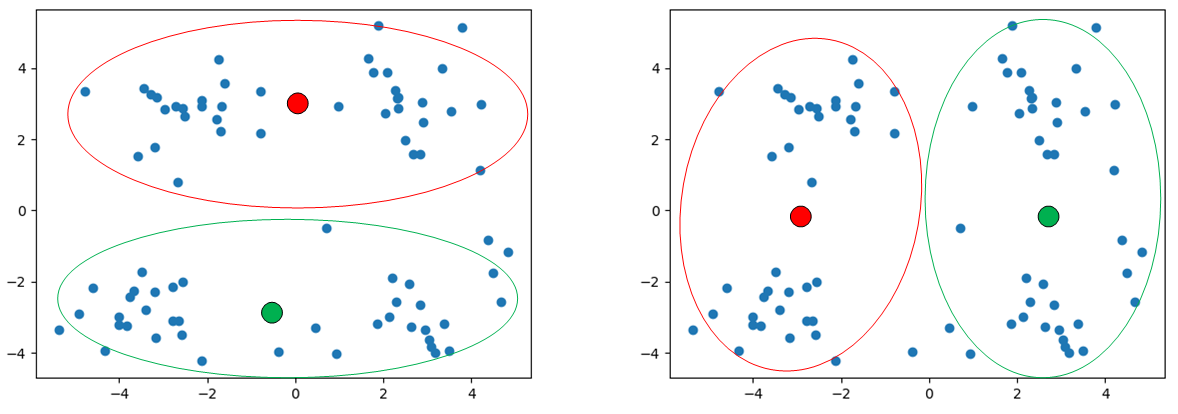
　　第一次随机选取的两个聚类中心为左边这张图的位置，那么结果可能分为上下两个簇，当第二次选取的为右边那张图片的位置时，可能最终的聚类结果为左右两个簇。

　　因此，聚类中心的初始位置，对于我们最终的结果影响很大。再比如：

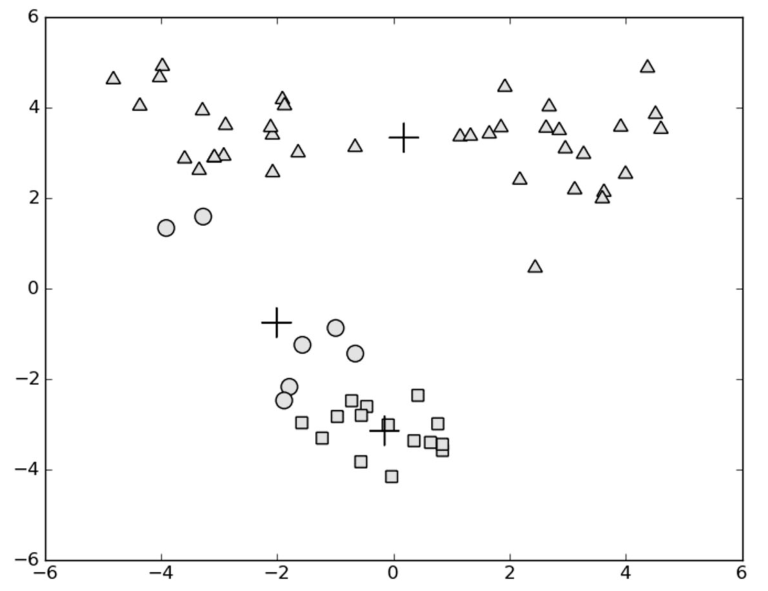
　　上面通过K-means将数据聚为3类，但由于聚类中心的问题，导致效果不好，“+”为最终聚类中心位置，此时聚类中心已不再更新。

　　这是因为K-means算法收敛到了局部最小值，而非全局最小值。

　　因此，我们需要一定的处理方法，来处理这样的问题：

　　一种最直观的做法是，我们通过多次初始化聚类中心，运行K-means聚类，得到多个结果，然后比较最后的损失（上面损失函数计算方法），选择其中最小的那一个结果。

　　然而这种对于k取值比较的少的时候可以这么做，但是如果k值过大，这样做也不会得到较好的改善。

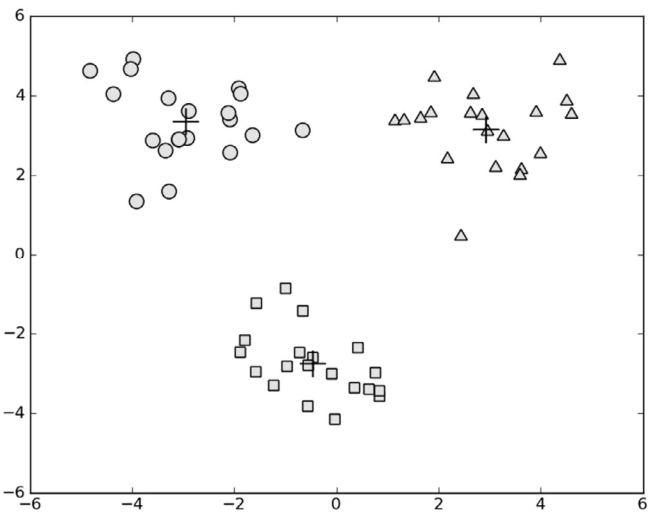
　　另一种做法是对生成的簇进行后处理，通过将具有最大的损失的那个簇，再分成两个簇，也就是对于损失最大的那个簇再运用一次K-means算法，将k值设为2；

　　但为了保证簇的总数不变，再将某两个簇进行合并，比如上面图中，将下面圆圈和方块进行合并，但是如果是一个多维数据，无法进行可视化时，我们无法查看应该去合并哪几个簇。

　　因此，可以有两种方法去衡量：（1）将最近的聚类中心对应的类进行合并；（2）合并两个使总的损失增加幅度最小的簇。

　　第一种方法是计算聚类中心（这里已经将最大的簇又分为两个簇）之间的距离，将最近的两个簇进行合并；

　　第二种方法需要计算合并两个簇之后的损失的大小，找出最佳的合并结果。

下面介绍一种利用上面划分簇的技术所改善的K-means算法。

二分K-Means算法

　　二分K-means算法是一种能够解决算法收敛到局部最小值的算法，算法思想是：首先将所有的点作为一个簇，然后分成2个，接下来，在其中选择一个簇进行划分，具体选择哪个，

　　要根据选择划分的簇能够使总损失降低程度最大的那个，此时簇被分为3个，然后重复上述过程，直到达到所指定的k个簇即停止。

　　具体算法过程如下：

　　　　1.将所有数据看做为一个簇；

　　　　2.当簇的总数目小于k时：

　　　　　　对于每一个簇：

　　　　　　　　（1）计算此时的损失；

　　　　　　　　（2）在此簇上采用K-means聚类（k=2）

　　　　　　　　（3）计算划分后的损失；

　　　　　　选择使划分后损失最小的簇，将其进行划分

　　上述过程中也可以选择损失最大的那个簇进行划分。

下面是具体实现过程：

def bi_kmeans(data, k, dist_measure=cal_dist):

    m = shape(data)[0]

    cluster_ass = mat(zeros((m, 2)))

    # 初始化聚类中心，此时聚类中心只有一个，因此对数据取平均

    centroid0 = mean(data, axis=0).tolist()[0]

    # 存储每个簇的聚类中心的列表

    centList = [centroid0]

    for j in range(m):

        cluster_ass[j, 1] = dist_measure(mat(centroid0), data[j, :]) ** 2

    while (len(centList)) < k:

        lowestSSE = inf

        for i in range(len(centList)):

            # 在当前簇中的样本点

            point_in_current_cluster = data[nonzero(cluster_ass[:, 0].A == i)[0], :]

            # 在当前簇运用kmeans算法，分为两个簇，返回簇的聚类中心和每个样本点距离其所属簇的中心的距离

            centroid_mat, split_cluster_ass = Kmeans(point_in_current_cluster, 2, dist_measure)

            # 计算被划分的簇，划分后的损失

            sse_split = sum(split_cluster_ass[:, 1])

            # 计算没有被划分的其它簇的损失

            sse_not_split = sum(cluster_ass[nonzero(cluster_ass[:, 0].A != i)[0], 1])

            # 选择最小的损失的簇，对其进行划分

            if sse_split + sse_not_split < lowestSSE:

                # 第i个簇被划分

                best_cent_to_split = i

                # 第i个簇被划分后的聚类中心

                best_new_centers = centroid_mat

                # 第i个簇的样本，距离划分后所属的类别（只有0和1）以及距离聚类中心的距离

                best_cluster_ass = split_cluster_ass

                lowestSSE = sse_split + sse_not_split

        # 把新划分出来的簇，属于1类的簇重新进行编号，编号为原先的总类别数目，比如原先有两类，选择一个进行划分后，又分成两类，等于1的那一类编号为2

        best_cluster_ass[nonzero(best_cluster_ass[:, 0].A == 1)[0], 0] = len(centList)

        # 同理，属于第0类的重新编号，编号为所选的那一类的编号

        best_cluster_ass[nonzero(best_cluster_ass[:, 0].A == 0)[0], 0] = best_cent_to_split

        # 将原来的聚类中心进行替换

        centList[best_cent_to_split] = best_new_centers[0, :]

        # 并加入新的1类的聚类中心

        centList.append(best_new_centers[1, :])

        # 将之前被选到划分的那一类的结果全部替换成被划分后的结果

        cluster_ass[nonzero(cluster_ass[:, 0].A == best_cent_to_split[0]), :] = best_cluster_ass

    return mat(centList), cluster_ass

2.2 K值的影响及其改进

　　K-means算法的K值需要人为给出所需要聚类的类别数目k，那么k的选择对于结果影响很大，通常k值的选择通常需要根据实际进行手动选择，比如给定一组身高和体重的数据，我们可以聚成三类（S、M、L）来指导生产。

　　还有一种方法用于选择k值的方法，成为“手肘法则”（elbow method），其原理很简单，就是通过设定不同的k值，然后画出每一个k值对应的损失，如图所示：

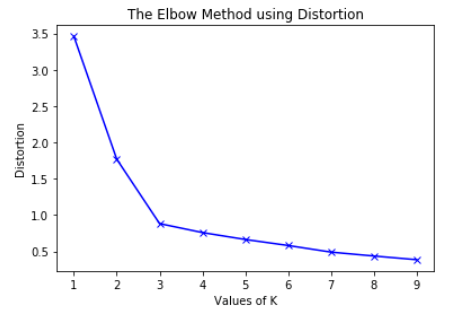
　　然后找出“手肘”的位置，就是最佳的聚类数目k。

　　这里有个问题，损失不应该是越小越好吗？理论上是这样的，但当我们把n个数据点聚成n个类别，此时损失为0，然而这并没有什么意义（类似于过拟合）。

　　因此我们选择“手肘”的位置，此时损失下降相较于后面下降速度较大，即k=3。

　　具体的实现这里不再说了，就是计算不同k值，然后计算Loss损失就可以了。这里补充一个关于能够自动选择k值的库：yellowbrick，代码很简单（参考https://www.zhihu.com/question/279825061/answer/1686762604）：

from sklearn.cluster import KMeans

from yellowbrick.cluster.elbow import kelbow_visualizer

from yellowbrick.datasets.loaders import load_nfl

x, y = load_nfl()

kelbow_visualizer(KMeans(random_state=4), x, k=(2, 10))

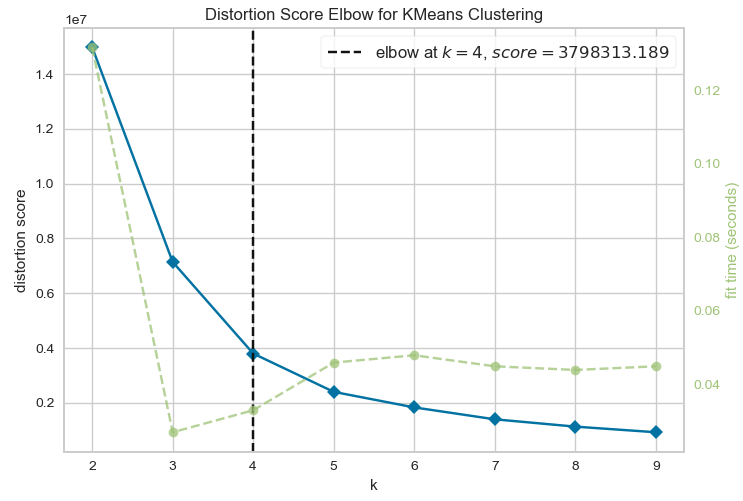
　　可以自动选出k值（k=4），而且画出的图也很好看。

　　上面就是K-means算法的基本内容，由于算法比较简单，内容不多，而且sklearn也带有Kmeans的工具包（上面那个例子里就是）。总的来说虽然K-means算法比较简单，但是用途还是比较广泛的。

最近事情比较多，学习进度有点慢~，后面会继续针对聚类算法做总结和学习，下一次主要对层次聚类和DBSCAN进行一个回顾和总结。