最大流最小割——bzoj1001狼抓兔子，洛谷P2598

前置知识

平面图

平面图就是平面上任意边都不相交的图。（自己瞎画的不算XD）

对偶图

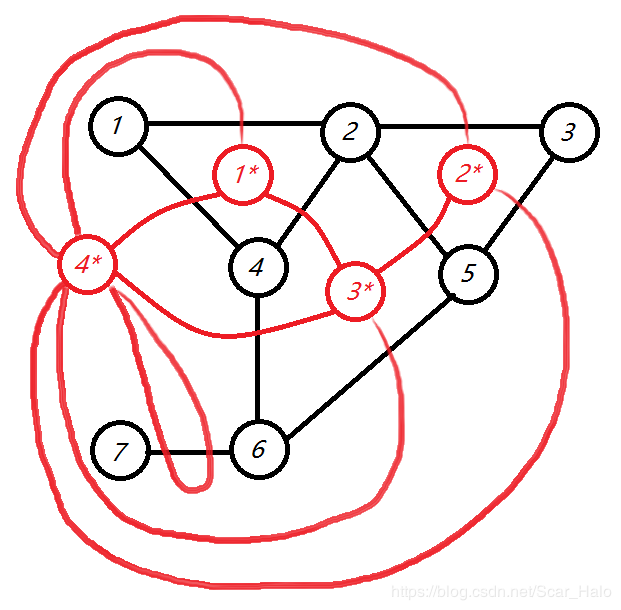
比如说这个图，我们发现平面图肯定会把平面分成不同的区域（感觉像拓扑图），并把这些区域当做每个点（不被包围的区域独自成点，如本图4*），给相邻的区域连上边，就转化成了一个对偶图（图中红色）

割

网络流的图中有两个点：原点和汇点。割就是删去的一些边使原点和汇点无法连接（不太严谨）

看题！bzoj1001

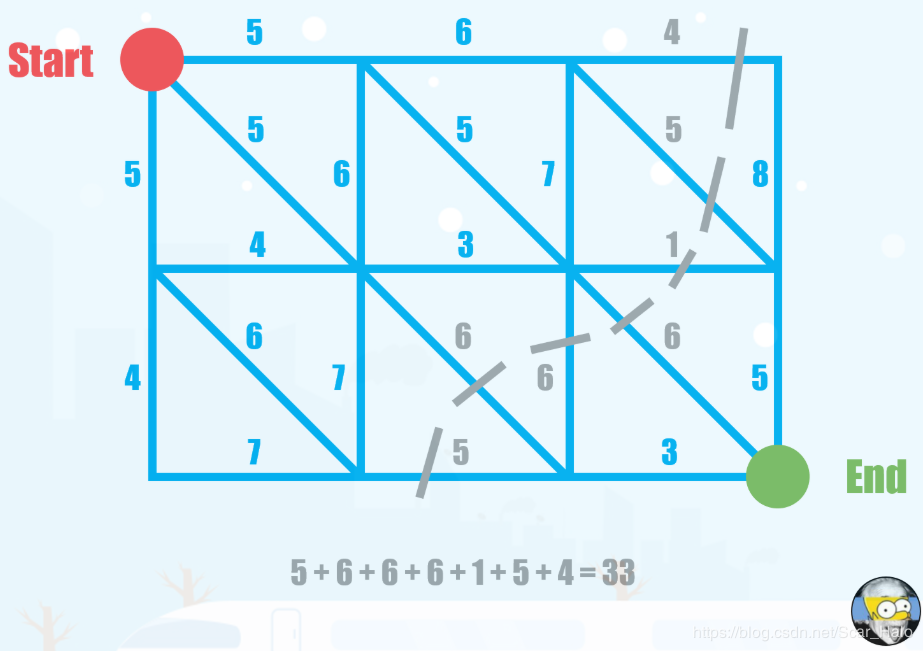
既然有了原点和汇点，那么就不能简单的把外部看做一个点了，我们把外部分成两个点——超级原点和超级汇点！

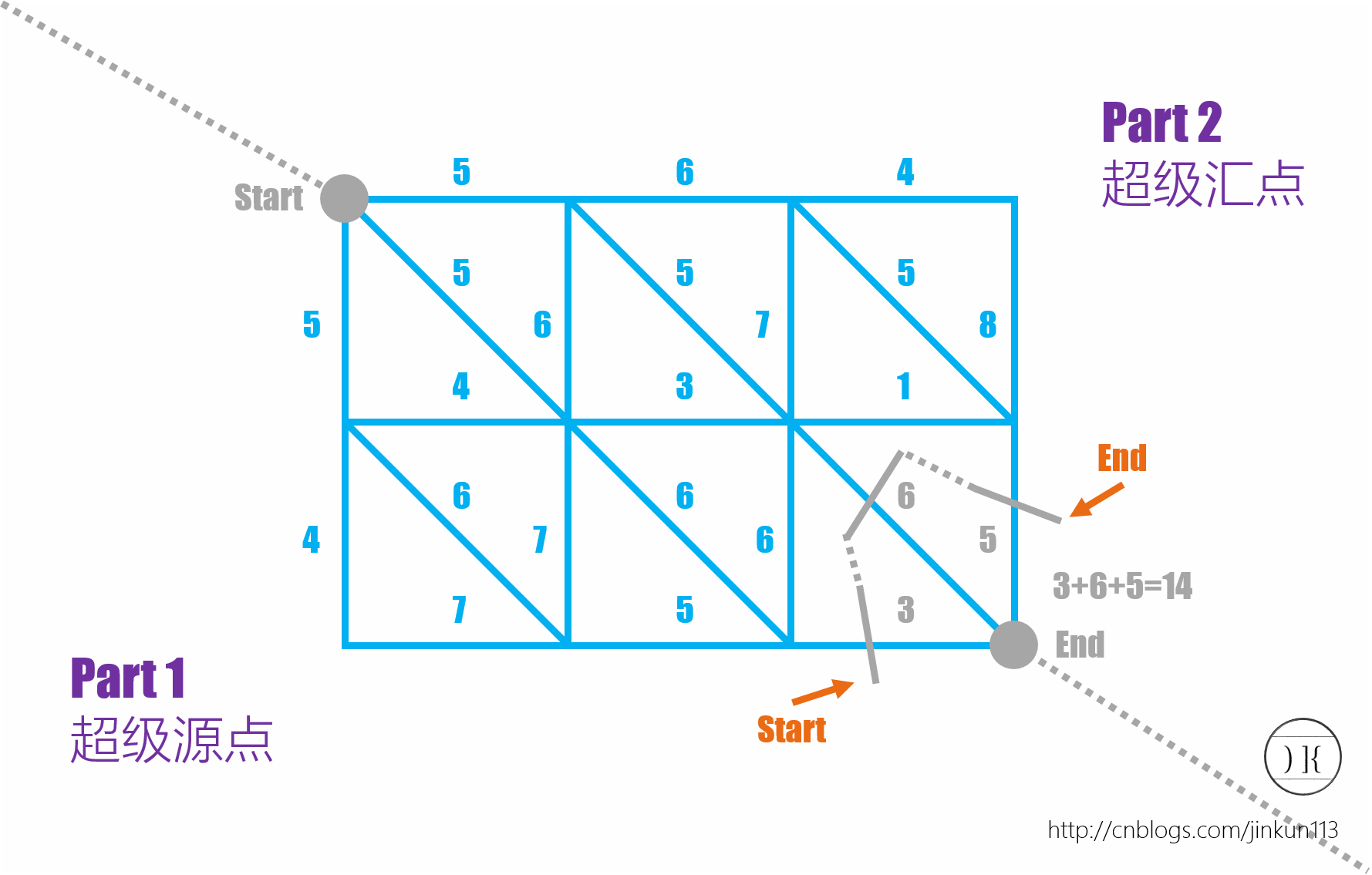
然后像上面一样建边，求对偶图的最短路就行了！！！

你问我如何判断对偶图的点之间割了哪些边？

emmm这就是它恶心的地方了——建图并不容易。不过，它给边的方式还是有点人性的。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cctype>
#include<cstring>
#include<utility>
#include<queue>
#include<functional>
#include<vector>
using namespace std;
inline int read()
{
    int x=0,w=0;char c=getchar();
    while(!isdigit(c))w|=c=='-',c=getchar();
    while(isdigit(c) )x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return w?-x:x;
}
const int maxn=3000000;
typedef pair<int,int> pii;
int n,m,node[1210][1210][2];
int ecnt,t[maxn<<1],nxt[maxn<<1],head[maxn<<1],val[maxn<<1];
inline void addedge(int from,int to,int dis)
{
    t[++ecnt]=to;nxt[ecnt]=head[from];head[from]=ecnt;val[ecnt]=dis;
    t[++ecnt]=from;nxt[ecnt]=head[to];head[to]=ecnt;val[ecnt]=dis;
}
int dis[maxn];
bool vis[maxn];
inline void dijkstra(int start,int end)
{
 
    memset(dis,0x3f3f3f3f,sizeof dis);
    priority_queue<pii,vector<pii >,greater<pii > > q;
    q.push(make_pair(0,start)),dis[start]=0;
    while(!q.empty())
    {
        int u=q.top().second;q.pop();
        if(vis[u])continue;
        vis[u]=1;
        for(int i=head[u];i;i=nxt[i])
        {
            int v=t[i],w=val[i];
            if(dis[v]>=dis[u]+w)
            {
                dis[v]=dis[u]+w;
                q.push(make_pair(dis[v],v));
            }
        }
    }
}
int main()
{
    int v=1;
    n=read()-1,m=read()-1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            for(int k=0;k<2;k++)
                node[i][j][k]=v++;
    int start=v++,end=v;
    for(int j=1;j<=m;j++)addedge(start,node[1][j][0],read());
    for(int i=1;i<=n-1;i++)
        for(int j=1;j<=m;j++)
            addedge(node[i][j][1],node[i+1][j][0],read());
    for(int j=1;j<=m;j++)addedge(end,node[n][j][1],read());
    /*横行*/
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m+1;j++)
            if(j==1)addedge(end,node[i][j][1],read());
            else if(j==m+1)addedge(start,node[i][j-1][0],read());
            else addedge(node[i][j-1][0],node[i][j][1],read());
    /*纵行*/
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            addedge(node[i][j][0],node[i][j][1],read());
    /*斜行*/
    dijkstra(start,end);
    printf("%d\n",dis[end]);
    return 0;
}

好了，以上只是针对bzoj1001的问题的解法。实际上，这个问题还有一些通用的解法（只不过出题人不想让大家用加强了数据）

不过上一道题我们也可以用下面的方式求出网络的最小割。

不过我们换一题XD

P2598狼和羊的故事

（反正狼就是nb）

通过读题，我们发现，这个orez想圈养狼真是了不起（姜戎都不敢这么干）

最大流最小割定理：网络的最大流等于最小割

证明也比较简单（但我不会严谨的），感性理解一下，最大流一定有一些边是满的，我们把这些边割了它就流不成了。对于其他的边，要么不是必经之路，要么边权不比同一条流上的最大流的边小，所以~~得证~~

那么这道题的话其他前辈已经讲得很好了，即求法就是

1. 将所有狼连到原点，边权INF
2. 将所有羊连到汇点，边权INF
3. 将所有点的四周加边，边权为1

这是一个对偶图的思想，相当于组成了一个网络，在这个网络中，只要点与点之间有边相连就相当于之间没有栅栏，所以一开始是全部连接的。我们要做的，就是砌栅栏把一些边断掉，使狼和羊分离。因为所有狼和所有羊都连在原点和汇点，这就相当于求最小割了。
（不知道讲清楚没有）

前面两个大家应该都清楚，边权INF相当于没有影响只是把所有狼/羊连在一起罢了。第三步就是连边：因为修一个栅栏需要1，所以边权为1，简直和对偶图一模一样（本来就是一个思想）
同样的，这里的难度就在于建边，建完求最大流就行了。

注意数组的大小。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cctype>
#include<utility>
#include<queue>
using namespace std;
inline int read()
{
    int w=0,x=0;char c=getchar();
    while(!isdigit(c))w|=c=='-',c=getchar();
    while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return w?-x:x;
}
namespace star
{
    const int maxn=100005,INF=0x3f3f3f3f;
    int n,m;
    int mapp[105][105];
    int ecnt=1,head[maxn],t[maxn<<1],nxt[maxn<<1],val[maxn<<1];
    inline void addedge(int from,int to, int dis)
    {
        t[++ecnt]=to;val[ecnt]=dis;nxt[ecnt]=head[from];head[from]=ecnt;
        t[++ecnt]=from;val[ecnt]=0;nxt[ecnt]=head[to];head[to]=ecnt;
    }
    int fx[]={0,1,0,-1},fy[]={1,0,-1,0};
    int cnt;
    int dep[maxn],start,end,cur[maxn];
    inline bool BFS()
    {
        queue<int> q;
        for(int i=1;i<=cnt;i++)dep[i]=-1,cur[i]=head[i];
        dep[start]=0;
        q.push(start);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            for(int i=head[u];i;i=nxt[i])
                if(val[i] and dep[t[i]]==-1)
                    dep[t[i]]=dep[u]+1,q.push(t[i]);
        }
        if(dep[end]==-1)return 0;
        return 1;
    }
 
    int DFS(int x,int flow)
    {
        if(x==end)return flow;
        int used=0;
        for(int i=cur[x];i;i=nxt[i])
        {
            cur[x]=i;
            int u=t[i];
            if(val[i] and dep[u]==dep[x]+1)
            {
                int w=DFS(u,min(val[i],flow-used));
                used+=w;
                val[i]-=w;
                val[i^1]+=w;
                if(used==flow)return flow;
            }
        }
        if(!used)dep[x]=-1;
        return used;
    }
    inline void build()
    {
        n=read(),m=read();
        cnt=0;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                mapp[i][j]=++cnt;
        start=++cnt,end=++cnt;
        for(int zp,i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                if((zp=read())==1)addedge(start,mapp[i][j],INF);
                else if(zp==2)addedge(mapp[i][j],end,INF);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                for(int k=0;k<4;k++)
                {
                    int xx=i+fx[k],yy=j+fy[k];
                    if(xx<1 or xx>n or yy<1 or yy>m)continue;
                    addedge(mapp[i][j],mapp[xx][yy],1);
                }
    }
    inline void work()
    {
        build();
        int ans=0;
        while(BFS())ans+=DFS(start,INF);
        printf("%d\n",ans);
    }
}
int main()
{
    star::work();
    return 0;
}