canvas实现任意正多边形的移动（点、线、面）

前言

我在上一篇文章简单实现了在canvas中移动矩形（点线面），不清楚的小伙伴请看我这篇文章：用canvas 实现矩形的移动（点、线、面）（1）。 ok,废话不多说，直接进入文章主题， 上一篇文章我留了很多问题，就是我在画步中移动我怎么知道我移动的是哪一个类型，到底是点还是线还是面， 这就是本篇文章要解决的问题。 读完本篇可以学到下面几点：

1. 判断点与点之间的距离

2. 判断点与直线的关系（叉乘的使用）

3. canvas中如何画出正n边形。（旋转）

其实我上面说了这么多，其实就是为了在2d图形做一个效果就是 snap ——吸附，判断当前点与当前画布上多边形的关系。

吸附——实现点

读者你可以思考下，如果要你去做你会怎么去做呢？ 假设画布上有很多多边形，还有很多点。有人说了，哪一个靠近它不就是哪一个。ok 你答对了，其实就是去判断当前点和画布上所有的点去比对，哪一个离的近，就是选中的哪一个点，这里会涉及到一个查询性能问题？ 有同学就会问如果画布中有很多点呢？我们难道就要一个个去遍历比较大小嘛，当然不是这里给大家科普一下一个空间几何索引算法Rbush

RBush是一个高性能JavaScript库，用于点和矩形的二维空间索引。它基于优化的R树数据结构，支持批量插入。

我后面有时间会带大家撸一遍Rbush的，这里我给出参考链接 有兴趣的同学自行了解下。本篇就不用Rbush，就用集合去存储数据了哈！ 这里还有一点需要强调的就是画布中的每一个点应该都每一个点都一个是实例，具有独特的id。 我们接下来就重新改造下：

const current = 0;
const map = new Map();
constructor(x,y) {
    this.x = x || 0;
    this.y = y || 0;
    this.id = ++current;
    map.set(this.id,[x,y]);
}
// 增加到Map上
add2Map() {
  pointMap.push(this)
  return this
}
//用来随机生成一个点
random(width,height){
    this.x = Math.random() * width;
    this.y = Math.random() * height;
    return this;
}
​
// 取绝对值
abs() {
    return [Math.abs(this.x), Math.abs(this.y)]
}
​
//计算两个点之间的距离
distance(p) {
    const [x,y] = this.clone().sub(p).abs();
    return Math.sqrt(x*x + y * y);
}
​

我又重新写了一个画多边形的方法代码如下：

// 画多边形
function drawAnyPolygon(points) {
    if(!Array.isArray(points)) {
        return;
    }
    ctx.strokeStyle = 'black'
    ctx.setLineDash([]); 
    ctx.beginPath();
    const start = points[0];
    ctx.moveTo(start.x,start.y)
    points.slice(1).forEach(item => {
        ctx.lineTo(item.x,item.y)
    })
    ctx.closePath()
    ctx.stroke()
}

这个没什么最重要的是什么呢，我们如何根据一个点去生成正多边形的点集合

CANVAS中如何画正多边形？

这里我们看下多边形的定义：

正多边形是指二维平面内各边相等，各角也相等的多边形，也叫正多角形。

去比较鼠标的点和画布中的点的距离了。我们先看第一部分根据类型生成点：

// 根据移动的类型重新生成点
function generatePointsByType(mousePoint,type = 'point',width = 200, height = 200) {
      const results = [];
      const { x, y } = mousePoint;
      const moveVec = end.clone().sub(start);
      const p1  =  new Point2d(x- width /2, y - height/2).add2Map();
      const p2 = new Point2d(x+ width / 2, y - height/2).add2Map();
      const p3 = new Point2d(x+ width / 2, y + height/2).add2Map();
      const p4 = new Point2d(x - width / 2, y + height/2).add2Map();
      return [p1,p2,p3,p4]
  }

这里有一点要注意的是就是p1,p2,p3,p4 满足的是顺时针，因为我们canvas画图是从左上----->左下的。 这一点大家在自己调试的要十分注意！！add2Map， 就是把点加入到Map中。我在上面补充上。我给出下一部分代码：比较鼠标的点和画布中的点之间的大小。

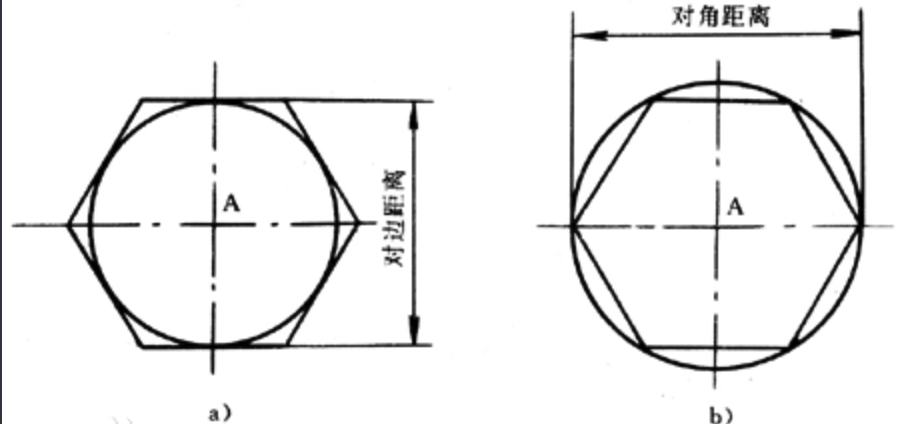
从图中我们可以得到： 正多形的形成 无非就是两种

1. 以当前点为圆心、画出一个外接圆、然后呢 根据边数进行等分

2. 以当前点为圆心、画出一个内接圆、然后呢 根据边数进行等分

原理我们知道了，应用到我们canvas怎么去实现呢？ 其实也很简单，我们以圆心和圆上的一点，作为起始的向量。然后不断地旋转 2π/n 的角度 就可以得到所有的点了。 有了点我们就可以画出正多边形了。 这里是外接圆算多边形的思路，至于内接圆怎么去算， 给大家一个课后思考题自己去想一下。 我给出以下代码实现：

第一部分点的绕着某一个中心点旋转的：

 rotate(center, angle) {
      const c = Math.cos( angle ), s = Math.sin( angle );
      const x = this.x - center.x;
      const y = this.y - center.y;
      this.x = x * c - y * s + center.x;
      this.y = x * s + y * c + center.y;
      return this;
​
  }

这里的大概思路向量的旋转然后在加上中心点的位置。 如果看不懂的话， 我给大家找一个推导过程： 传送门

第二部分就是如果生成多边形的顶点了：

function getAnyPolygonPoints(start, end, n = 3) {
    const angle = (Math.PI * 2) / n
    const points = [end]
    for (let i = 1; i < n; i++) {
      points.push(
        end
          .clone()
          .rotate(start.clone(), angle * i)
          .add2Map()
      )
    }
    return points
  }

接下我就给大家看下 n = 5|10 |20 |50 的 这些正多边形。然后你会发现随着边数的增加，我们画的多边形越越像个圆了。

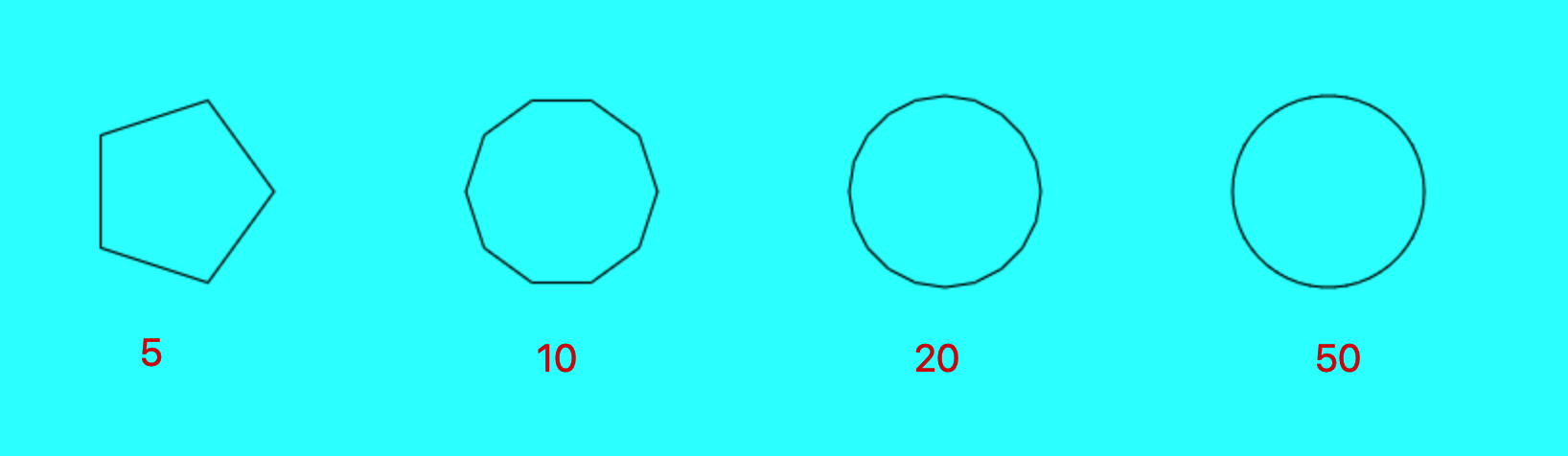
有没有解锁你们的新世界？各位读者们。看到这里如果觉得对你有帮助的话。点个赞继续往下看吧。 还有一些数学方法的介绍。

实现任意正多边形点的移动

我们设想鼠标不停地在画布上移动，我肯定哪一个点离我近，我就去选择哪一个点。 所以也就是不停的比较鼠标移动的点和已经存在的点的距离做判断。ok思路有了，我给出以下代码：

function calcClosestPoint() {
    const minMap = []
    for (let value of pointMap) {
      const dis = value.distance(start.clone())
      minMap.push({ ...value, dis })
    }
    // 找出最近的的一个点
    const sort = minMap.sort((a, b) => a.dis - b.dis)
    return sort[0]
}

这段代码肯可能要讲的就是两点之间求距离？ 这个就很简单了，就是两个坐标相减求绝对值，然后开方。一般人肯定会这么想对吧，一开始我也是这么想的。 这么想没问题， 但是其实我不不需要开方，我们要比较的是距离。这里会有一个性能小优化。因为你要开方，然后cpu又去计算，如果画布中点的数量过多呢，并且数字很大的情况下。代码如下：

distance(p) {
  const [x, y] = this.clone().sub(p).abs()
  return x * x + y * y
}
​
distanceSq(p) {
  const [x, y] = this.clone().sub(p).abs()
  return Math.sqrt(x * x + y * y)
}

找到最小的点，我们就可以重复上一篇文章实现移动了。这里就不做过多讲解了，不清楚的小伙伴，可以去看过上一篇文章。 给出以下代码：

//画出任意多边形 满足顺时针方向
  function drawAnyPolygon(points) {
    if (!Array.isArray(points)) {
      return
    }
    ctx.strokeStyle = 'black'
    ctx.setLineDash([])
    ctx.beginPath()
    // 存在移动的点
    if (movePoint.length > 0) {
      const moveVec = end.clone().sub(start)
      points = points.map((item) => {
        if (item.equal(movePoint[0])) {
          return item.clone().add(moveVec)
        }
        return item
      })
    }
    ctx.moveTo(points[0].x, points[0].y)
    points.slice(1).forEach((item) => {
      ctx.lineTo(item.x, item.y)
    })
    ctx.closePath()
    ctx.stroke()
  }
​
canvas.addEventListener('click', (e) => {
  if (e.altKey) {
    isMove = false
    return
  }
  isMove = !isMove
  const x = e.clientX
  const y = e.clientY
  start = new Point2d(x, y)
  movePoint.length = 0
  movePoint.push(calcClosestPoint())
  isSelect = true
})

这里我点击鼠标的以下就确定移动的点 和移动向量的起点，movePoint 其实是所有要移动的点。直接看效果图吧。

实现任意正多边形线的移动

点的移动我们实现了,我们鼠标的点的那一刻，我们该如何确定点击的是线呢，这也归咎到一个数学问题？ 就是比较点到直线的距离， 点到直线的距离，第一种解法就是直线方程去求解。 直线的直线方程是什么？

求点到直线的距离方法1

设直线 L 的方程为Ax+By+C=0，点 P 的坐标为（x0,y0），则点 P 到直线 L 的距离为：

同理可知，当P（x0,y0），直线L的解析式为y=kx+b时，则点P到直线L的距离为

考虑点(x0,y0,z0)与空间直线x-x1/l=y-y1/m=z-z1/n，有d=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)

也就是两个点算出斜率和截距，但是要考虑直线与Y轴的特殊情况，也就是斜率无穷大的时刻。 这时候的距离就是x坐标相减。这样我们可以计算点到直线的距离，然后比较找出距离最小的线，接着找出移动的点就可以了。但这不是最优解，

求点到直线的距离方法2

首先我问一个问题哈？ 向量的叉乘的几何意义是什么， 就是两个向量围成的平行四边形的面积。 我们计算点到直线的距离不就是计算，平行四边形的高嘛， 所以只要算出面积再除以底边就可以算出点到直线的距离了。 哈哈哈哈，是不是再一次被数学的魅力征服了。我给大家看个图吧：

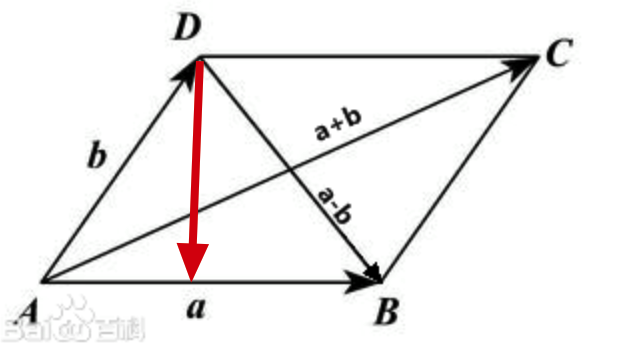
红色的线就是点到直线的距离。 我们直接开始coding了，理论有了直接开干。

首先写一个点转为线段的一个方法，因为我们是首尾相连，所以点的个数，最后一个应该是和开始点相同的。

function points2Segs(points) {
    const start = points[0]
    points.push(start)
    const segs = []
    points.forEach((point, index) => {
      if (index !== points.length - 1) {
        segs.push([point, points[index + 1]])
      }
    })
    return segs
}

叉乘的方法如下：

cross(v) {
   return this.x * v.y - this.y * v.x
}

计算点到直线的距离如下：

function pointDistanceToLine(target, line) {
  const [start, end] = line
  const vec1 = start.clone().sub(target)
  const vec2 = end.clone().sub(target)
  return vec1.clone().cross(vec2) / start.clone().distanceSq(target)
}
// 找出最近的线
function calcClosestLine() {
  let minMap = []
  segs.forEach((line) => {
    const dis = pointDistanceToLine(start, line)
    minMap.push({
      dis,
      line,
    })
  })
  minMap = minMap.sort((a, b) => a.dis - b.dis)
  // 找出最近的直线然后将点放入到movePoint 中其实就好了
  movePoint.push(...minMap[0].line)
}

移动那边代码改写一下：

 if (movePoint.length > 0) {
    const moveVec = end.clone().sub(start)
    points = points.map((item) => {
      // 线的移动对应的是两个点 面的话应该就是所有的点
      if (item.equal(movePoint[0]) || item.equal(movePoint[1])) {
        return item.clone().add(moveVec)
      }
      return item
    })
  }

直接来看效果：

完美实现很感谢你还能看到这里。 到这里因为点和线其实都会了，面就是所有的点移动这个是没什么难度的，后面大家可以自己去练习一下。

总结

本篇文章主要是介绍了2d 下图形的移动， 点线面。 本质上都是点的移动，加上一个移动向量。核心就是这个，其实还有很多东西是需要大家慢慢体会的。一个闭合区域的形成，点的顺序，肯定是首尾相连的，按照某一个方向。还有就是对于叉乘、点乘的一些理解。 结合到实现项目中可以灵活运用。本篇文章的所有代码都在我的github，如果大家觉得看完对你有帮助的话，可以star一下。 最后最后的还是希望大家点个赞和评论。 知识输出不易，对图形感兴趣的话可以关注我的公众号： 前端图形 持续分享canvas、svg、webgl知识。