C++数据结构之二叉查找树（BST）

C++数据结构之二叉查找树（BST）

二分查找法在算法家族大类中属于“分治法”，二分查找的过程比较简单，代码见我的另一篇日志，戳这里！因二分查找所涉及的有序表是一个向量，若有插入和删除结点的操作，则维护表的有序性所花的代价是O(n)。

就查找性能而言，二叉查找树和二分查找不分伯仲，但是，就维护表的有序性而言，二叉排序树无须移动结点，只需修改指针即可完成插入和删除操作，且其平均的执行时间均为O(lgn)，因此更有效。二叉查找树，顾名思义，是一种可以用来二分查找的树数据结构，其左孩子比父节点小，右孩子比父节点大，还有一个特性就是”中序遍历“可以让结点有序。在对关键字进行查找的时候，根据关键字与根节点的关键字比较的结果，分别选择继续与其左子树或者右子树进行比较，直到找到所查找的关键字或者访问节点的左右子树不存在（没找到关键字）则退出！

二叉查找树的主要操作有：插入关键字，查找关键字，删除关键字。下面分别对这三个步骤做详细描述和算法实现。

为了方便，我将二叉查找树实现为一个类，结构如下：

typedef struct Node_
{
    struct Node_ *parent;
    struct Node_ *left;
    struct Node_ *right;
    T data;
}Node;

class BinaryTree
{
public:
    BinaryTree():root(NULL){};
    ~BinaryTree();
    bool insertNode(T data);
    bool deleteNode(T data);
    Node* findNode(T data);
private:
    Node *root;
};

1. 插入关键字的过程如下所示：

插入过程的代码如下：

bool BinaryTree::insertNode(T data)
{
    Node *x = NULL, *current, *parent;

    /***********************************************
    *  allocate node for data and insert in tree  *
    ***********************************************/

    /* find x's parent */
    current = root;
    parent = NULL;
    while (current) {
        if (compEQ(data, current->data)) return true;
        parent = current;
        current = compLT(data, current->data) ?
            current->left : current->right;
    }

    /* setup new node */
    if ((x = (Node*)malloc(sizeof(*x))) == 0)
    {
        cout << "Insufficient memory (insertNode)!" << endl;
        return false;
    }
    x->data = data;
    x->parent = parent;
    x->left = NULL;
    x->right = NULL;

    /* insert x in tree*/
    if(parent)
        if(compLT(x->data, parent->data))
            parent->left = x;
        else
            parent->right = x;
    else
        root = x;

    return true;
}

其中的compEQ和compLT为2个宏定义，用来比较两个关键字的大小。

2. 查找关键字的过程比较简单，和二分查找方法类似，代码如下：

Node* BinaryTree::findNode(T data)
{
    /*******************************
    *  find node containing data  *
    *******************************/

    Node *current = root;
    while(current != NULL)
        if(compEQ(data, current->data))
            return current;
        else
            current = compLT(data, current->data) ?
                current->left : current->right;
    return NULL;
}

3. 删除关键字的过程分为2种情况讨论：单孩子的情况和左右孩子的情况。

1> 单孩子情况分析：

如果删除的节点有左孩子那就把左孩子顶上去，如果有右孩子就把右孩子顶上去，so easy！如图所示：

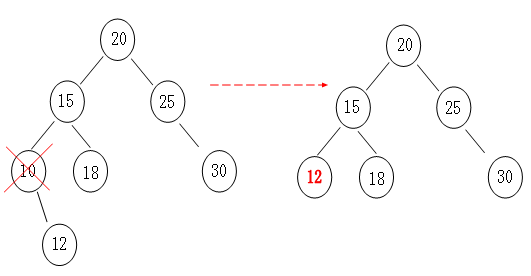
2> 左右孩子情况分析：

首先可以这么想象，如果我们要删除一个数组的元素，那么我们在删除后会将其后面的一个元素顶到被删除的位置，如下图所示：

那么二叉树操作同样也是一样，我们根据“中序遍历（inorder tree walk）”找到要删除结点的后一个结点，然后顶上去就行了，原理跟“数组”一样一样的。

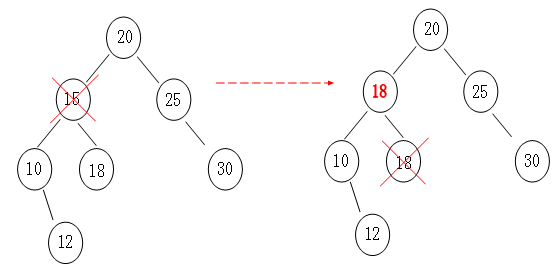
好了，贴代码：

bool BinaryTree::deleteNode(T data)
{
    Node* pNode = findNode(data);
    if (pNode == NULL)
    {
        cout << "Cannot find this data in BST!" << endl;
        return false;
    }

    Node *x, *y;
    /* find tree successor */
    if (pNode->left == NULL || pNode->right == NULL)
        y = pNode;
    else {
        y = pNode->right;
        while (y->left != NULL) y = y->left;
    }

    /* x is y's only child */
    if (y->left != NULL)
        x = y->left;
    else
        x = y->right;

    /* remove y from the parent chain */
    if (x) x->parent = y->parent;
    if (y->parent)
        if (y == y->parent->left)
            y->parent->left = x;
        else
            y->parent->right = x;
    else
        root = x;

    /* y is the node we're removing */
    /* z is the data we're removing */
    /* if z and y are not the same, replace z with y. */
    if (y != pNode) {
        y->left = pNode->left;
        if (y->left) y->left->parent = y;
        y->right = pNode->right;
        if (y->right) y->right->parent = y;
        y->parent = pNode->parent;
        if (pNode->parent)
            if (pNode == pNode->parent->left)
                pNode->parent->left = y;
            else
                pNode->parent->right = y;
        else
            root = y;
        free (pNode);
    }
    else {
        free (y);
    }
    return true;
}

好了，二叉查找树的代码告一段落，我们在来分析一下二叉查找树的插入过程，假如有以下序列：<4, 17, 16, 20, 37, 38, 43>，则会生成如下所示二叉树：

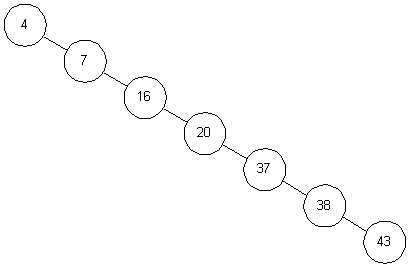
这已经完全退化成了一个单链表，势必影响到关键字的查找过程。不过总会有解决办法的，下一篇博客我将继续这个话题，对普通二叉树经过旋转，即使用平衡二叉树，使其保持最坏复杂度在O(logN)。

谢谢大家的阅读，希望能够帮到大家！PS：文章中部分图片利用了博客园另外一篇文章的插图（戳这里）！

Published by Windows Live Write!

作者： 薛定谔の喵 
出处： http://www.cnblogs.com/berlin-sun/ 
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接，否则保留追究法律责任的权利。

 

 

标签: 二分查找, BST, 二叉查找树, 二叉平衡树, 数据结构