数据结构录 之 单调队列&单调栈。

　　队列和栈是很常见的应用，大部分算法中都能见到他们的影子。

　　而单纯的队列和栈经常不能满足需求，所以需要一些很神奇的队列和栈的扩展。

　　其中最出名的应该是优先队列吧我觉得，然后还有两种比较小众的扩展就是单调队列和单调栈。

　　先来看一个问题，给一个长度为N的数列，a1，a2。。。aN，然后给一个k<=N，求输出b1，b2。。。bN这N个数，其中 bi=max( aj | j<=i && j>i-k && j>0 )。

　　比较朴素的想法是用一个Nk复杂度的循环来求，但是这样的话如果N很大的话就太慢了。

　　然后还有一种想法是维护一个BST，然后for循环从左到右，依次加入到BST里面，如果某个数超出了k的范围，就从BST中删除。

　　伪代码如下：

 void getans() {
     BST tree;

     for(int i=,j=;i<=N;++i) {
         tree.insert(a[i]);
         while(j<=i-k) {
             tree.erase(a[j]);
             --j;
         }
         cout<<tree.max()<<endl;
     }
 }

　　这样的话因为每个数只insert一次，最多erase一次，所以复杂度是NlogN的，已经很不错了。

　　但是BST比较高级，所以速度并不快，那么能不能根据这个问题的特点来设计一种更快的数据结构来解决？

　　先看这个问题，如果for循环从左到右来求b的话，就像是有个长度为k的框框一次次向右移动，每次求框内的最大值。

　　

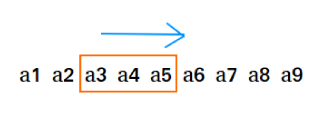
　　如果类比到队列的话，就是for循环的时候每次push一个数在队尾，然后把最前面那个超出的数pop出来，然后求队列内的最大值就行了。

　　但是一般的队列并不能求最大值，就需要一些扩展型的队列了。

　　单调队列就是队列内所有数都是单调递增的或者递减的。下面按照从队首到队尾递减的队列来讨论。

　　先看看push(x)：

　　　　如果当前队列为空的话，直接push进去就行。

　　　　如果当前队列末尾的数比x大，那么直接放到队尾，这时仍然是单调的。

　　　　如果末尾的数比x小的话，就扔掉队尾的数，然后再重复上面的步骤push(x)。

　　　　比如队列中是  5 4 2 1，然后push 3 进去的话，就把1和2扔掉，变成5 4 3，如果再push 7 进去的话，就把5 4 3 扔掉，队列变成了 7 。

　　然后pop的话和一般队列没有区别。

　　然后这个数据结构如果应用到这个问题上的话，看看答案是否是对的。

　　for循环从左到右，然后每次push当前的ai，然后判断如果队首的元素的位置超出了框框，就pop出来扔掉。然后这是bi就等于pop完之后队首的数。

 struct Queue {
     int val[MaxN],pos[MaxN];
     int first,last;

     void init() {
         first=last=;
     }

     void push(int v,int p) {
         while(last-first> && val[last-]<=v) --last;
         val[last]=v;
         pos[last++]=p;
     }

     void pop() {
         if(last-first>) ++first;
     }

     int firstPos() {
         return pos[first];
     }

     int firstVal() {
         return val[first];
     }
 };

 void getans() {
     Queue que;
     que.init();

     for(int i=;i<=N;++i) {
         que.push(a[i],i);
         while(que.firstPos()<=i-k) que.pop();
         cout<<que.firstVal().val<<endl;
     }
 }

　　先来看看这样对不对，首先队列是单调的，所以队首的数一定是最大的，这个数在失效的时候，在他位置前面的所有数也一定都失效了，而他位置后面的所有数还没失效，仍然符合最大的前面，也就是最大的仍然还在队列中没有被扔掉。所以下一次询问的时候仍然答案是对的。

　　然后看看复杂度如何，每个数只push了一次，然后最多会被扔掉一次，所以虽然push里面有while循环，但是这N个数每个最多被遍历一次然后就被扔掉了，所以for循环N次下来，均摊的复杂度是O（1）的对于每个push和pop操作，所以总复杂度是O（N）的。

　　然后这就是单调栈，单调栈和单调队列区别不大，都是每次push的时候要维护单调性。

　　有一道题目 POJ 2796 ，需要先进行转化然后在使用单调栈来解决。

　　单调栈和单调队列在大部分情况下是一种工具，对于一些问题能够优化到N的复杂度，这样会比logN快很多。所以其实有些情况下不用这个，用其他的数据结构也是可以做的。