样品GA的良好理解
遗传算法演示样本手册模拟
为了更好地理解遗传算法的计算过程,法的各
个主要运行步骤。
例:求下述二元函数的最大值:
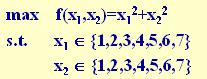
(1) 个体编码
遗传算法的运算对象是表示个体的符号串,所以必须把变量 x1, x2 编码为一种
符号串。
本题中。用无符号二进制整数来表示。
因 x1, x2 为 0 ~ 7之间的整数。所以分别用3位无符号二进制整数来表示。将它
们连接在一起所组成的6位无符号二进制数就形成了个体的基因型。表示一个可
行解。
比如,基因型 X=101110 所相应的表现型是:x=[ 5。6 ]。
个体的表现型x和基因型X之间可通过编码和解码程序相互转换。
(2) 初始群体的产生
遗传算法是对群体进行的进化操作。须要给其淮备一些表示起始搜索点的初始
群体数据。
本例中,群体规模的大小取为4,即群体由4个个体组成。每一个个体可通过随机
方法产生。
如:011101,101011,011100,111001
(3) 适应度汁算
遗传算法中以个体适应度的大小来评定各个个体的优劣程度,从而决定其遗传
机会的大小。
本例中,目标函数总取非负值,而且是以求函数最大值为优化目标。故可直接
利用目标函数值作为个体的适应度。
(4) 选择运算
选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有很多其它的机会遗传到下一代
群体中。
本例中。我们採用与适应度成正比的概率来确定各个个体拷贝到下一代群体中
的数量。其详细操作过程是:
• 先计算出群体中所有个体的适应度的总和 fi ( i=1.2,…,M );
• 其次计算出每一个个体的相对适应度的大小 fi / fi ,它即为每一个个体被遗传
到下一代群体中的概率。
• 每一个概率值组成一个区域,所有概率值之和为1;
• 最后再产生一个0到1之间的随机数。根据该随机数出如今上述哪一个概率区
域内来确定各个个体被选中的次数。
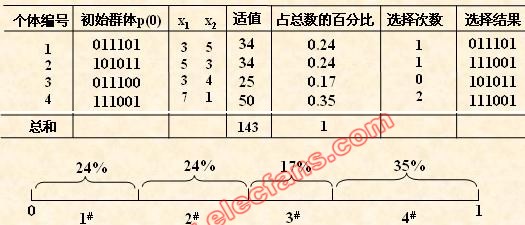
(5) 交叉运算
交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交换某
两个个体之间的部分染色体。
本例採用单点交叉的方法,其详细操作过程是:
• 先对群体进行随机配对;
• 其次随机设置交叉点位置。
• 最后再相互交换配对染色体之间的部分基因。
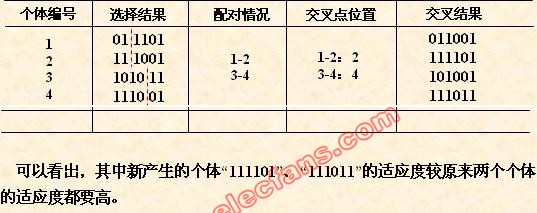
(6) 变异运算
变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进
行改变,它也是产生新个体的一种操作方法。
本例中,我们採用基本位变异的方法来进行变异运算。其详细操作过程是:
• 首先确定出各个个体的基因变异位置。下表所看到的为随机产生的变异点位置,
当中的数字表示变异点设置在该基因座处;
• 然后按照某一概率将变异点的原有基因值取反。
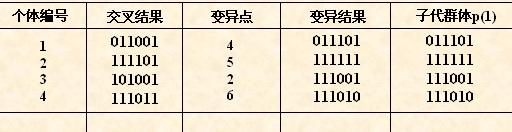
对群体P(t)进行一轮选择、交叉、变异运算之后可得到新一代的群体p(t+1)。
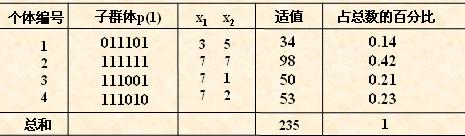
从上表中可以看出,群体经过一代进化之后,其适应度的最大值、平均值都得
到了明显的改进。
其实。这里已经找到了最佳个体“111111”。
[注意]
须要说明的是。表中有些栏的数据是随机产生的。这里为了更好地说明问题。
我们特意选择了一些较好的数值以便可为了得到更好的结果,在实际操作过程中
有可能需要一定数目的周期,以达到最佳结果的人才。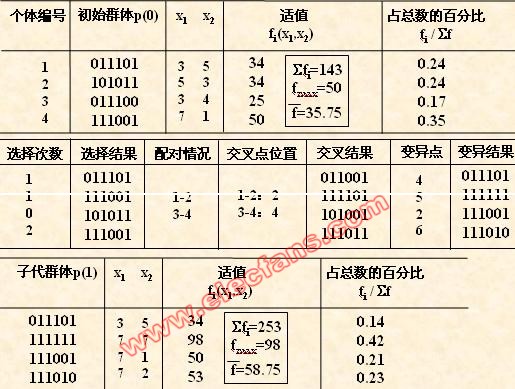
样品GA的良好理解的更多相关文章
- HttpClient 图讲解明
大家刚看这个名字一定会想问这是什么东东,在这我特意百度百科了下 HTTP 协议可能是如今 Internet 上使用得最多.最重要的协议了,越来越多的 Java 应用程序须要直接通过 HTTP 协议来訪 ...
- 深入理解PHP内核(九)变量及数据类型-静态变量
原文链接:http://www.orlion.ga/251/ 通常静态变量是静态分配的,他们的生命周期和程序的生命周期一样长,只有在程序退出后才结束生命周期,这和局部变量相反,有的语言中全局变量也是静 ...
- 深入理解PHP内核(六)哈希表以及PHP的哈希表实现
原文链接:http://www.orlion.ga/241/ 一.哈希表(HashTable) 大部分动态语言的实现中都使用了哈希表,哈希表是一种通过哈希函数,将特定的键映射到特定值得一种数据 结构, ...
- GA遗传算法解析
LinJM @HQU 谈及遗传算法,我首先想到的就是孟德尔的豌豆实验.当然,遗传算法实质上并不能用豌豆实验说明,豌豆实验探讨了分离定律和自由组合定律,而遗传算法所借鉴的并不是这两个定律.遗传算法,简 ...
- 遗传算法GA
遗传算法(Genetic Algorithms,GA)是一种全局优化方法,它借用了生物遗传学的观点,通过自然选择.遗传.变异等作用机制,实现种群中个体适应性的提高,体现了自然界中“物竞天择.适者生存” ...
- Python 操作 GA API 指南
因为需要写一个 Blog Feature 的缘故,所以接触了下 GA 的 Python API,发现 G 家的 API 不是那么直观,比较绕,但是,在使用过程中发现其实 G 家的 API 设计挺有意思 ...
- 通过Visualizing Representations来理解Deep Learning、Neural network、以及输入样本自身的高维空间结构
catalogue . 引言 . Neural Networks Transform Space - 神经网络内部的空间结构 . Understand the data itself by visua ...
- 理解OpenShift(7):基于 Prometheus 的集群监控
理解OpenShift(1):网络之 Router 和 Route 理解OpenShift(2):网络之 DNS(域名服务) 理解OpenShift(3):网络之 SDN 理解OpenShift(4) ...
- JMeter学习(七)聚合报告之 90% Line 正确理解(转载)
转载自 http://www.cnblogs.com/yangxia-test 90% Line 参数正确的含义: 虽然,我的上面理解有一定的道理,显然它是错误的.那看看JMeter 官网是怎么说的? ...
随机推荐
- 让XP系统支持GPT硬盘
转自 http://article.pchome.net/content-1324506-all.html 1XP系统还不过时 教你完美征服3TB硬盘回顶部 原作者:沈洁 随着高清1080p片源的普及 ...
- jquery easyui Accordion的使用
<html> <head> <script src="jquery-easyui/jquery.min.js"></script> ...
- C/C++ Resources
C/C++ Resources 一.C/C++相关资源 语言标准及文档● ISO C99http://www.open-std.org/JTC1/SC22/WG14/www/docs/n1124.pd ...
- STL 之 queue、priority_queue 源代码剖析
/* * Copyright (c) 1994 * Hewlett-Packard Company * * Permission to use, copy, modify, distribute an ...
- 用Python制作游戏外挂(上)
源地址:http://eyehere.net/2012/python-game-bot-autopy-1/ 悲剧成我这样的人,我知道肯定不止我一个,所以我一点都不悲伤:-( 所以我打开了4399小游戏 ...
- GrabCut--Opencv篇
最近因为工作需要,需要实现一个Grabcut函数.Opencv已经提供此函数,今天把opencv的例程拿出来跑了一下,对于简单的背景实现效果还不错. OpenCV中的GrabCut算法是依据<& ...
- Delphi默认窗体随想
Delphi中新建一个Form或者Frame时,它的字体都是西文习惯,这样就有可能造成在其他机器上由于字体的原因,窗体十分不美观.怎样才能为Delphi设置一个默认窗体,让它的字体Font符合中国习惯 ...
- Oracle dump 分析secondary key
验证secondary key 含有主键列数据 SQL> select object_name,object_id,OBJECT_TYPE from user_objects; OBJECT_N ...
- linux-sfdisk 使用方法
功能说明:硬盘分区工具程序. 语 法:sfdisk [-?Tvx][-d <硬盘>][-g <硬盘>][-l <硬盘>][-s <分区>][-V < ...
- liGDX life_cycle (生命周期)
本文章翻译自libGDX官方wiki,,转载请注明出处:http://blog.csdn.net/kent_todo/article/details/37940489 libGDX官方网址:http: ...
