LCS 小结

转载链接：http://www.cnblogs.com/PJQOOO/p/3897745.html

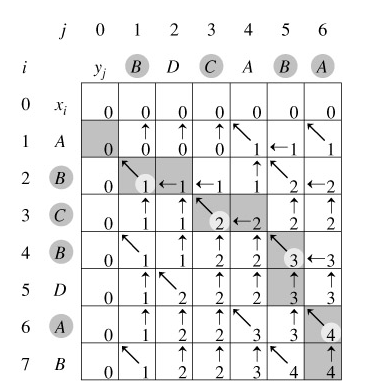
第一步：先计算最长公共子序列的长度。

实现第一步：

设一个C[i][j]: 保存X_i与Y_j的LCS的长度。

设X = { x1~xm },Y = { y1~yn }及它们的最长子序列Z = { z1~zk }则：

1、若 xm = yn ， 则 zk = xm = yn，且Z[k-1] 是 X[m-1] 和 Y[n-1] 的最长公共子序列

2、若 xm != yn ，且 zk != xm , 则 Z 是 X[m-1] 和 Y 的最长公共子序列

3、若 xm != yn , 且 zk != yn , 则 Z 是 Y[n-1] 和 X 的最长公共子序列

子问题的递归结构：

当 i = 0 , j = 0 时 , c[i][j] = 0

当 i , j > 0 ; xi = yi 时 , c[i][j] = c[i-1][j-1] + 1

当 i , j > 0 ; xi != yi 时 , c[i][j] = max { c[i][j-1] , c[i-1][j] }

第二步：根据长度，然后通过回溯求出最长公共子序列。

实现代码：

 #include <stdio.h>
 #include <string.h>
 #include <math.h>
 #include <limits.h>
 #include <algorithm>
 #include <iostream>
 #include <ctype.h>
 #include <iomanip>
 #include <queue>
 #include <map>
 #include <stdlib.h>
 using namespace std;

 char a[],b[],dp[][];

 int LCS(int n,int m){
     int i,j;
     int len=max(n,m);
     for(i=;i<=len;i++){
         dp[i][]=;
         dp[][i]=;
     }
     for(i=;i<=n;i++){
         for(j=;j<=m;j++){
             if(a[i-]==b[j-]){
                 dp[i][j]=dp[i-][j-]+;
             }
             else{
                 dp[i][j]=max(dp[i-][j],dp[i][j-]);
             }
         }
     }
     return dp[n][m];
 }

 int main()
 {
     cin>>a;
     cin>>b;
     int n=strlen(a);
     int m=strlen(b);
     int k=LCS(n,m);
     cout<<k<<endl;
     int i=n-,j=m-,count=k;
     while(count!=){
         if(a[i]==b[j]){
             cout<<a[i];
             i--;
             j--;
             count--;
         }
         else if(dp[i][j-]>dp[i-][j]){
             j--;
         }
         else{
             i--;
         }
     }
     cout<<endl;
 }