洛谷P5022 旅行 题解

---

前面几个代码都是部分分代码，最后一个才是AC了的，所以最后一个有详细注释

这是提高组真题，233有点欧拉回路的感觉。

---

题目大意：

一个 连通 图，双向边 ，无重边 ， 访问图中所有点并依次记录经过的点的编号。求记录的编号字典序最小。

---

题目数据分析

题目中有 M 条边，而 M 有两种情况： M = N 或者 M = N- 1 。

---

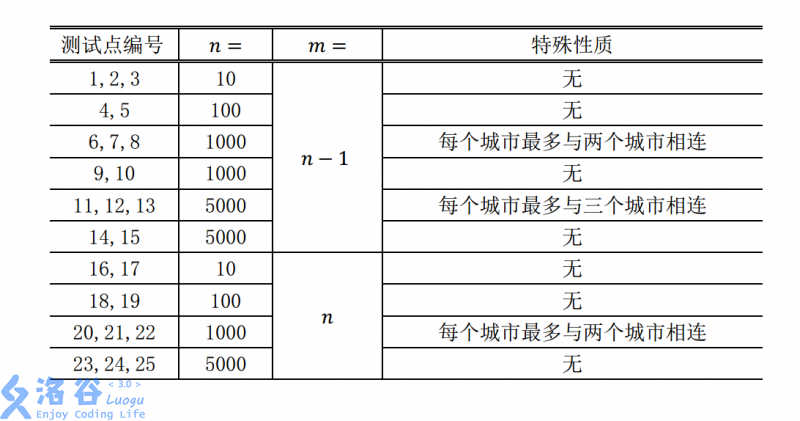
现在我们将 M = N的情况叫做情况一 ，M = N - 1叫做情况二

情况一和情况二分析

情况二：我们都知道，一棵生成树有N - 1条边，且要保证连通，那么显而易见，情况二是一棵 生成树 。根据生成树的特性，我们可以得知，情况二 不会形成环。

情况一：情况一，不过是在情况二上多了一条边。但是还是要保证连通、无重边，故情况二是 在一棵生成树上多了一条表——有且只有一个环。

根据题意，可以保证数据 一定 会是以上两种情况。

---

那么现在我们的问题是如何解决情况一和情况二。

情况二

很简单，一棵生成树，只需要使用爆搜即可。

由于情况二是生成树，所以个人认为DFS更好使用。

那怎么搜？

一颗生成树，是可以以树中任意一个点为 \(Root\) （根节点）。而题目要求了是要字典序最小，显然 以 1 为根节点开始DFS的答案会更优秀

此时，只需要从 \(1\) 到 \(N\) 循环，判断目前循环到的点与当前到达的点是否连通，并再继续DFS即可。

血的教训：由于情况二是遍历一棵树，所以不要回溯！

情况二代码如下：

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 5000 + 10;

int n,m;
bool dis[MAXN][MAXN];
int in[MAXN],ans[MAXN],cnt;
bool b[MAXN];

inline int read(){
    int f = 1, x = 0;
    char c = getchar();

    while (c < '0' || c > '9')
    {
        if (c == '-')
            f = -1;
        c = getchar();
    }

    while (c >= '0' && c <= '9')
    {
        x = x * 10 + c - '0';
        c = getchar();
    }

    return f * x;
}

void dfs(int now){
    ans[++cnt] = now;
    b[now] = true;
    for(int i = 1;i <= n; i++){
        if(b[i])continue;
        if(!dis[now][i])continue;
        b[i] = true;
        dfs(i);
    }
}

int main(){
    n = read(),m = read();
    for(int i = 1;i <= m; i++){
        int x = read(),y = read();
        dis[x][y] = dis[y][x] = true;
    }
    dfs(1);
    for(int i = 1;i <= n; i++){
        cout<<ans[i]<<" ";
    }
}

情况二只占60分。那么其他40分就是情况一了

题目都要由简入难。情况二解决，情况一就有思路可想=借鉴了。

现在情况一不过是在情况二上面多了一个环。还可以使用DFS么？很明显不行。

由于所有点只能访问一次（退回来的不算），环中必须会有一条边无法访问。

为什么

因为对于一棵树，dfs是每个节点与其父亲连接的边都可以搜到的；

但是现在多了一条边，又要满足题目要求——每个点除了第一次访问和回溯外，不能再次访问

所以在情况二上多加了一条边，那么一定有一条边无法访问到。

所以呢？

我们只需要找到唯一的环，在环内任意枚举一条边，删去那一条边，再运行情况二的DFS，最后取最优解即可

注意：情况一DFS与情况二DFS不同，情况一由于有环，所以要回溯。

那么我们现在的问题就是要找环。并准确知道哪些点在环内。

如何找环？

并查集？很明显不行。它只能判断两个点是否是一个父亲且一个点在不在环内，很麻烦求出准确的环。

Tarjan？太麻烦了......

那么就用——拓扑排序！

并查集、Tarjan、拓扑排序之后都会在本人Blog中介绍

我们拓扑排序删边时，只要标记当前队列的头，拓扑之后那些没被标记过的，也就是没被拓扑排序的、在环内的点。

但是拓扑排序只有入度为0的点才加入队列么？题目说是无向图，一条边两个点入度都++，那不就没有入度为0的点了么？

没关系，我们只需要将入度和出度加起来当做度数来，再判断度数是不是1即可。

为什么？

因为拓扑排序在累计入度的时候，环的入口入度一定为 \(3\) ，一个父亲，另外的是环内的点自带的入度。删去与环连接的那一条边，入口点的入度还是会有大于一，故无法进队处理。

那么情况一和情况二的合集代码如下

先不要提交下面的代码！因为没有前面说的注释，所有后面还有没讲完的

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 5000 + 10;

int n,m,cur;
int in[MAXN],ans[MAXN];
int res[MAXN];

vector<int>nei[MAXN];
bool dis[MAXN][MAXN];
struct Line{
    int xx,yy;
}line[MAXN];

bool b[MAXN],use[MAXN];

inline int read(){
    int f = 1, x = 0;
    char c = getchar();

    while (c < '0' || c > '9')
    {
        if (c == '-')
            f = -1;
        c = getchar();
    }

    while (c >= '0' && c <= '9')
    {
        x = x * 10 + c - '0';
        c = getchar();
    }

    return f * x;
}

void init(){
    n = read(),m = read();

    for(int i = 1;i <= m; i++){
        int x = read(),y = read();
        dis[x][y] = dis[y][x] = true;
        nei[x].push_back(y);
        nei[y].push_back(x);
        in[x]++,in[y]++;
        line[i] = (Line){x,y};
    }
    return;
}

void out(){
    for(int i = 1;i <= n; i++){
        cout<<ans[i]<<" ";
    }
    cout<<"\n";
    return;
}

void new_ans(){
    for(int i = 1;i <= n; i++){
        ans[i] = res[i];
    }
}

void work() {
    if(ans[1] == 0){
    	new_ans();
    	//out();
    	return;
    }

    for(int i = 1; i <= n; i++) {
        if(res[i] == ans[i])
            continue;
        else if(res[i] < ans[i]) {
            new_ans();
            //out();
            return;
        }
        //out();

        return;
    }
}

void Topo(){
    queue<int>q;

    for(int i = 1;i <= n; i++){
        if(in[i] == 1){
            q.push(i);
            use[i] = true;
        }
    }

    while(!q.empty()){
        int tot = q.front();
        int len = nei[tot].size();

        q.pop();
        use[tot] = true;

        for(int i = 0;i < len; i++){
            int next = nei[tot][i];
            in[next]--;

            if(in[next] == 1){
                q.push(next);
                use[next] = true;
            }
        }
    }
}

void dfs_plan_1(int now){
    ans[++cur] = now;
    b[now] = true;
    for(int i = 1;i <= n; i++){
        if(b[i])continue;
        if(!dis[now][i])continue;
        b[i] = true;
        dfs_plan_1(i);
    }
}

void dfs(int now){
    res[++cur] = now;
    b[now] = true;
    for(int i = 1;i <= n; i++){
        if(b[i])continue;
        if(!dis[now][i])continue;
        b[i] = true;
        dfs(i);
        b[i] = false;
    }
    b[now] = false;
} 

int main(){
    init();

    for(int i = 1; i <= n; i++) {
        sort(nei[i].begin(), nei[i].end());
    }

    if(m == n - 1){
        dfs_plan_1(1);
        out();
        return 0;
    }

    Topo();

    for(int i = 1;i <= m; i++){
        int x = line[i].xx;
        int y = line[i].yy;

        if(use[x] || use[y])continue;

        dis[x][y] = dis[y][x] = false;
        cur = 0;

        dfs(1);

        work();
        dis[x][y] = dis[y][x] = true;
    }

    out();
    return 0;
}

为什么TLE了几个点？

不是叫你别提交么

因为这种做法枚举了所有点，会导致超时，所以我们现在只需要维护每个点和它相邻的边，枚举那些边就好。

---

那么现在思路非常明确了：

那么其实上面就是一个重要的知识——

基环图

没完，代码下面还有东西

#include<bits/stdc++.h>//万能头
using namespace std;

const int MAXN = 5000 + 10;//定义常量 

int n,m,cur;//n、m与题目相对应，cur记录答案累加用途
int in_out[MAXN],ans[MAXN];//ans为答案，in_out为度数（即入读加上出度）
int res[MAXN];//用于临时存目前计划，在更新ans与res判断 

vector<int>nei[MAXN];//动态数组用于记录邻居，这里用于优化时间复杂度
bool dis[MAXN][MAXN];//邻接矩阵，用来优化判断两个点的边目前又没有删
struct Line{//记录边的结构体
	int xx,yy;//起始点和终止点
}line[MAXN];

bool b[MAXN],use[MAXN];//b用于在DFS时看是否搜过了 ,use记录该店是否在环内 

inline int read(){//读入优化
    int f = 1, x = 0;
    char c = getchar();

    while (c < '0' || c > '9')
    {
        if (c == '-')
            f = -1;
        c = getchar();
    }

    while (c >= '0' && c <= '9')
    {
        x = x * 10 + c - '0';
        c = getchar();
    }

    return f * x;
}

void init(){//读入函数
	n = read(),m = read();//读入点和边 

	for(int i = 1;i <= m; i++){//读入边
		int x = read(),y = read();
		dis[x][y] = dis[y][x] = true;//将x与y的邻接矩阵更新
		nei[x].push_back(y);//将y压入x的邻居
		nei[y].push_back(x);//将x压入y的邻居
		in_out[x]++,in_out[y]++;//将x和y的度数++
		line[i] = (Line){x,y};//保存边
	}

	//for(int i = 1;i <= n; i++){
	//	for(int j = 1;j <= n; j++){
	//		cout<<dis[i][j]<<" ";
	//	}
	//	cout<<endl;
	//}
	//调试函数 

	return;
}

void out(){//输出函数，单独拿出来是用于调试用的
	for(int i = 1;i <= n; i++){
		cout<<ans[i]<<" "; //循环输出答案
	}
	cout<<"\n";
	return;
}

void new_ans(){//更新答案
	for(int i = 1;i <= n; i++){
		ans[i] = res[i];
	}
}

void work() {//用于判断目前方案与答案哪个更优
    if(ans[1] == 0){//如果目前答案为空，直接记录
    	new_ans();//更新答案
    	//out();
    	return;//这里一定要返回
    }

    for(int i = 1; i <= n; i++) {//逐次比较哪个更优
        if(res[i] == ans[i])//如果相同则继续
            continue;
        else if(res[i] < ans[i]) {//当前方案更优
            new_ans();//更新
            //out();
            return;
        }
	//	out();

        return;
    }
}

void Topo(){//基环图(与拓扑排序差不多)
	queue<int>q;//定义队列 

	for(int i = 1;i <= n; i++){//将度数为1的雅图队列
		if(in_out[i] == 1){
			q.push(i);
			use[i] = true;//标记不在环中
		}
	}

	while(!q.empty()){//还可以继续做
		int tot = q.front();//取队首
		int len = nei[tot].size();

		q.pop();
		use[tot] = true;//标记不在环中 

		for(int i = 0;i < len; i++){//依次删除度数
			int next = nei[tot][i];//下一个点
			in_out[next]--;

			if(in_out[next] == 1){//压入队列
				q.push(next);
				use[next] = true;
			}
		}
	}
}

void dfs_plan_1(int now){//用于情况二的DFS，这里不要回溯
	ans[++cur] = now;//直接更新答案
    b[now] = true;//标记
    int len = nei[now].size(); 

    for(int i = 0;i < len; i++){//循环
		int next = nei[now][i];

        if(b[next])continue;
        if(!dis[now][next])continue;
        b[next] = true;
        dfs_plan_1(next);
    }
}

void dfs(int now){//用于情况一的DFS，这里要回溯
	res[++cur] = now;//更新当前方案
	b[now] = true;
	int len = nei[now].size();
	for(int i = 0;i < len; i++){
		int next = nei[now][i];

		if(b[next])continue;
		//cout<<now<<" "<<next<<" "<<dis[i][next]<<endl;
		if(!dis[now][next])continue;
		b[next] = true;
		//cout<<next;
		dfs(next);
		b[next] = false;
	}
	b[now] = false;
	//cout<<"end."<<endl;
} 

int main(){
	init();//读入 

	for(int i = 1; i <= n; i++) {
		//这里很巧妙，从小到大排列邻居，优化
        sort(nei[i].begin(), nei[i].end());
    }

	if(m == n - 1){//情况二
		dfs_plan_1(1);
		out();
		return 0;
	}

	//情况一 

	Topo();//基环图 

	for(int i = 1;i <= m; i++){//枚举删边
		int x = line[i].xx;
		int y = line[i].yy;

		if(use[x] || use[y])continue;//有一个点不在环中就跳过 

		//cout<<i<<"line:"<<x<<" "<<y<<" "<<dis[x][y]<<endl;

		dis[x][y] = dis[y][x] = false;//删边
		cur = 0;

		dfs(1);//DFS 

		work();//更新答案
		dis[x][y] = dis[y][x] = true;//恢复边
	}

	out();//输出
	return 0;
}

基环图的处理方法

来都来了，听听吧

基换图如上面说的，就是一颗树多了一条边，形成了唯一的环。处理方法也会像上面说的，Topo排序找环、DFS即可