洛谷P1265 公路修建题解

题目描述

某国有n个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

（1）如果两个或以上城市申请修建同一条公路，则让它们共同修建；

（2）如果三个或以上的城市申请修建的公路成环。如下图，A申请修建公路AB，B申请修建公路BC，C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请；

（3）其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相：连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入格式

第一行一个整数n，表示城市的数量。(n≤5000)

以下n行，每行两个整数x和y，表示一个城市的坐标。(-1000000≤x，y≤1000000)

输出格式

一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

输入输出样例

输入 #1复制

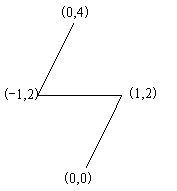
4
0 0
1 2
-1 2
0 4

输出 #1复制

6.47

说明/提示

修建的公路如图所示：

解析：

MST裸题(不接受挨打)

由于是稠密图，所以采用了Prim算法
(稀疏图最好用克鲁斯卡尔)
对任意两个点都求出距离
然后对其跑一遍最小生成树
但是注意n的范围是5000，而大小限制为125MB

题目本身不难，但是会一直MLE，所以需要优化

我这里有三个代码，不同的分数

第一个是裸的开 5000*5000 double数组的Prim算法可以跑出80分的好成绩(不开O2)。、

第二个是裸的克鲁斯卡尔算法，不开O2估计70分，开了O2稳定80分，运气好的话就是90分

第三个就是Prim，与第一个Prim不同的是会减少大量的冗余运算，具体体现就是把 5000 * 5000 的数组取消掉

只会在需要计算的时候才会计算，将大大减少时间和内存，，，所以就AC了。

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<string>
 #include<algorithm>
 #include<iomanip>
 #include<cstdlib>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<vector>
 #define LL long long
 #define re register
 #define INF 0x7fffffff
 #define Max 5002
 #define D double
 inline int read()
 {
     int s=,f=-;char ch=getchar();
     while(ch<''||ch>'') {if(ch=='-') f=-;ch=getchar();}
     while(ch>=''&&ch<='') s=s*+ch-'',ch=getchar();
     return s*f;
 }
 int n;D ans=0.0,g[Max][Max],dis[Max];
 bool vis[Max]={};
 struct edge {
     D x,y;
 }t[Max];
 D Dis(D x1,D y1,D x2,D y2)
 {
     return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
 }
 int main()
 {
     scanf("%d",&n);
     for(re int i =  ; i <= n ; ++ i) g[i][i]=,scanf("%lf%lf",&t[i].x,&t[i].y);
     for(re int i =  ; i <= n ; ++ i)
         for(re int j = i+ ; j <= n ; ++ j)
             g[i][j]=g[j][i]=Dis(t[i].x,t[i].y,t[j].x,t[j].y);
     int pos;vis[]=;
     for(re int i =  ; i <= n ; ++ i) dis[i]=g[][i];
     for(re int i =  ; i < n ; ++ i) {
         pos=;
         for(re int j =  ; j <= n ; ++ j) {
             if(vis[j]==) continue;
             if(!pos || dis[j] < dis[pos]) pos=j;
         }
         vis[pos]=;
         ans+=dis[pos];
         for(re int j =  ; j <= n ; ++ j) {
             if(vis[j]==) continue;
             dis[j]=std::min(dis[j],g[pos][j]);
         }
     }
     printf("%.2lf",ans);
     return ;
 }

80分裸的Prim

 // luogu-judger-enable-o2
 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<string>
 #include<algorithm>
 #include<iomanip>
 #include<cstdlib>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<vector>
 #define LL long long
 #define re register
 #define Max 5000*5000/2
 #define D double
 inline int read()
 {
     int s=,f=-;char ch=getchar();
     while(ch<''||ch>'') {if(ch=='-') f=-;ch=getchar();}
     while(ch>=''&&ch<='') s=s*+ch-'',ch=getchar();
     return s*f;
 }
 int n,pa[Max];D ans=;
 struct edge {
     D x,y;
 }t[Max];
 struct DIS {
     D dis;
     int from,to;
     friend bool operator<(DIS a,DIS b) {
         return a.dis<b.dis;
     }
 }e[Max];
 int find(int x)
 {
     if(x!=pa[x]) pa[x]=find(pa[x]);
     return pa[x];
 }
 void join(int x,int y)
 {
     x=find(x);y=find(y);
     pa[y]=x;
 }
 D Dis(D x1,D y1,D x2,D y2)
 {
     return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
 }
 int main()
 {
     scanf("%d",&n);int cnt=;
     for(re int i =  ; i <= n ; ++ i) pa[i]=i,scanf("%lf%lf",&t[i].x,&t[i].y);
     for(re int i =  ; i <= n ; ++ i)
         for(re int j = i+ ; j <= n ; ++ j)
             e[++cnt].dis=Dis(t[i].x,t[i].y,t[j].x,t[j].y),e[cnt].from=i,e[cnt].to=j;
     int k=;
     std::sort(e+,e++cnt);
     for(re int i =  ; i <= cnt ; ++ i) {
         int x=e[i].from,y=e[i].to;D t=e[i].dis;
         if(find(x)!=find(y)) join(x,y),ans+=t;
         if(k==n-) break;
     }
     printf("%.2lf",ans);
     return ;
 }

开O2或许是90分或许是80分，看你是否脸黑

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<string>
 #include<algorithm>
 #include<iomanip>
 #include<cstdlib>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<vector>
 #define LL long long
 #define re register
 #define INF 0x7fffffff
 #define Max 5002
 #define D double
 inline int read()
 {
     int s=,f=-;char ch=getchar();
     while(ch<''||ch>'') {if(ch=='-') f=-;ch=getchar();}
     while(ch>=''&&ch<='') s=s*+ch-'',ch=getchar();
     return s*f;
 }
 int n;D ans=0.0,dis[Max];
 bool vis[Max]={};
 struct edge {D x,y;}t[Max];
 D Dis(D x1,D y1,D x2,D y2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));}
 int main()
 {
     scanf("%d",&n);
     for(re int i =  ; i <= n ; ++ i) dis[i]=INF,scanf("%lf%lf",&t[i].x,&t[i].y);
     int pos;dis[]=;
     for(re int i =  ; i <= n ; ++ i) {
         D m=INF*1.0;
         for(re int j =  ; j <= n ; ++ j)
             if(dis[j] < m && !vis[j]) m=dis[j],pos=j;
         vis[pos]=;
         ans+=m;
         for(re int j =  ; j <= n ; ++ j) {
             if(vis[j]==) continue;
             D d=Dis(t[pos].x,t[pos].y,t[j].x,t[j].y);
             dis[j]=std::min(dis[j],d);
         }
     }
     printf("%.2lf",ans);
     return ;
 }

AC 代码