Luogu-P1450 [HAOI2008]硬币购物-完全背包+容斥定理

Luogu-P1450 [HAOI2008]硬币购物-完全背包+容斥定理

---

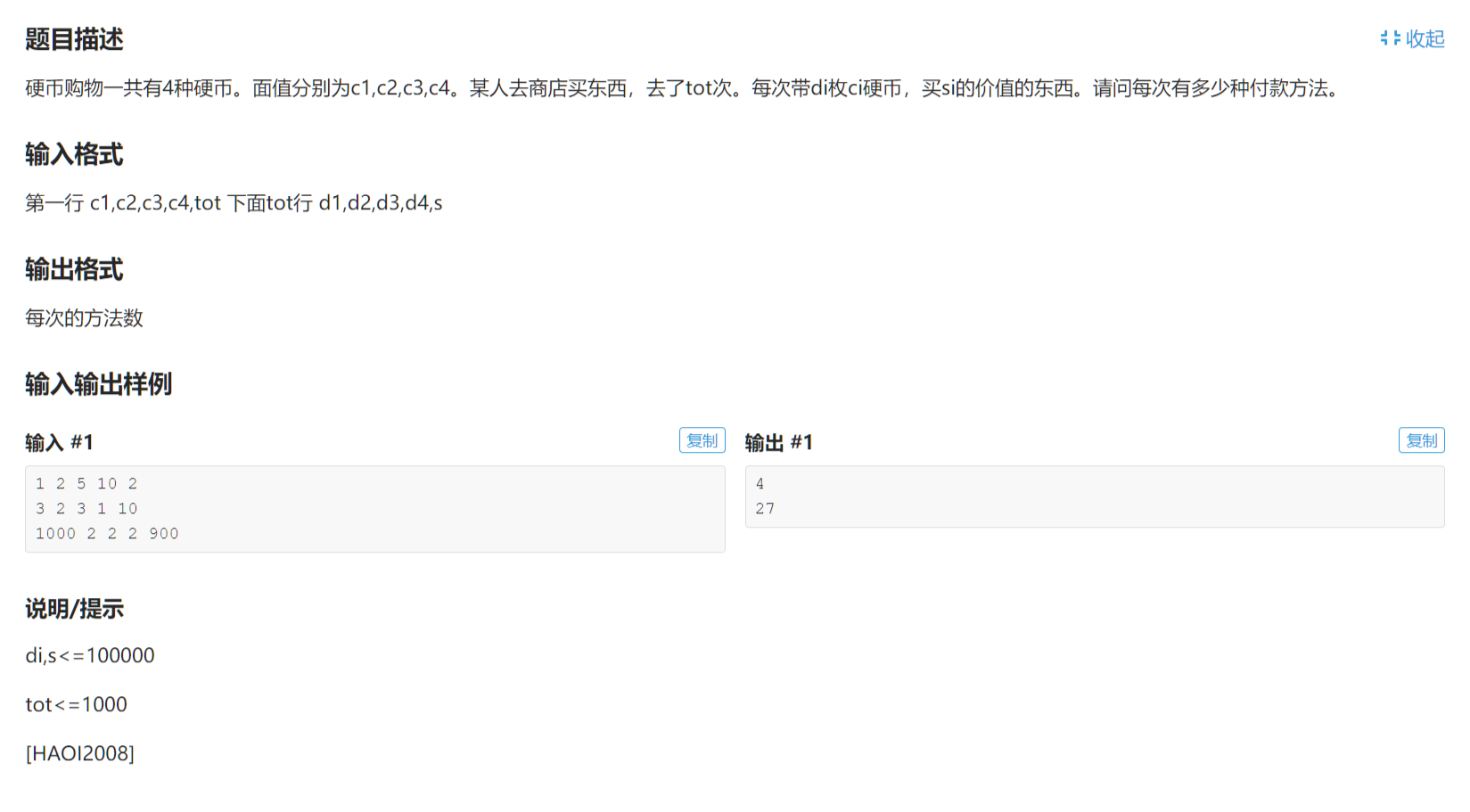
【Problem Description】

略

【Solution】

上述题目等价于：有\(4\)种物品，每种物品有\(d_i\)个，且每种物品的体积为\(c_i\)，问有多少种方法装满容量为\(s\)的背包？可以很容易想到跑多重背包即可，但是发现复杂度为\(O(4V\cdot n)\)。不可行。

题目要求的东西也等价于求以下等式有多少组满足条件的解：

\[c_1\cdot x_1+c_2\cdot x_2+c_3\cdot x_3+c_4\cdot x_4=s\\且0\le x1\le d_1,\ 0\le x_2\le d_2,\ 0\le x_3\le d_3,\ 0\le x_4\le d_4
\]

如果学过容斥定理的，就可以看出来这是容斥定理的一个模型。

即先不考虑\(x_1,x_2,x_3,x_4\)的上界限制条件，即每种物品有无限多个，那么就可以跑完全背包求得所有的方案数，令\(\overline A_1,\overline A_2,\overline A_3,\overline A_4\)分别代表\(0\le x1\le d_1,\ 0\le x_2\le d_2,\ 0\le x_3\le d_3,\ 0\le x_4\le d_4\)的条件，那么我们要求的就是满足\(\overline A_1\cap \overline A_2\cap \overline A_3\cap \overline A_4\)的方案数。有容斥原理公式得：

\[|\overline A_1\cap \overline A_2\cap \overline A_3\cap\overline A_4 |=|S|-(|A_1|+|A_2|+|A_3|+|A_4|)\\+(|A_1\cap A_2|+|A_1\cap A_3|+|A_1\cap A_4|+|A_2\cap A_3|+|A_2\cap A_4|+|A_3\cap A_4|)\\-(|A_1\cap A_2\cap A_3|+|A_1\cap A_2\cap A_4|+|A_1\cap A_3\cap A_4|+|A_2\cap A_3\cap A_4|)\\+(|A_1\cap A_2\cap A_3\cap A_4)\\
\]

对于\(|A_1|\)，我们知道\(A_1\Leftrightarrow x_1\ge d_1+1\)。所以\(|A_1|\)就表示\(x_1\ge d_1+1,\ x_2,x_3,x_4\ge 0\)时以下等式的解的个数：

\[c_1\cdot x_1+c_2\cdot x_2+c_3\cdot x_3+c_4\cdot x_4=s\\且x_1\ge d_1+1, x_2,x_3,x_4\ge 0
\]

令\(z_1=x_1-(d_1+1)，z_2=x_2,z_3=x_3,z_4=x_4\)，则原式变为在\(z_1,z_2,z_3,z_4\ge 0\)的条件下，求以下等式解的个数：

\[c_1\cdot z_1+c_2\cdot z_2+c_3\cdot z_3+c_4\cdot z_4=s-(d_1+1)\\且x_1,x_2,x_3,x_4\ge0
\]

预处理\(10^5\)以内容量为\(i\)方案数\(dp[i]\)。则\(|A_1|=dp[s-(d_1+1)]\)。同理\(|A_i|=dp[s-(d_i+1)]\)。

对于\(|A_1\cap A_2|\)等其他子集，也用类似方法转换为完全背包的做法。因为物品数只有\(4\)个，所以用位运算枚举子集，偶加奇数减即可。详细请看代码。复杂度为\(O(4V+2^4\cdot n)\)。

---

【Code】

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f
#define maxn 100005
int dp[maxn];
int c[5],d[5];
void CompleteBack(int V,int vol){ //完全背包
	for(int j=vol;j<=V;j++){
		dp[j]=dp[j]+dp[j-vol];
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>c[0]>>c[1]>>c[2]>>c[3];
	dp[0]=1;
	for(int i=0;i<4;i++){
		CompleteBack(maxn-5,c[i]);
	}
	int n;cin>>n;
	while(n--){
		cin>>d[0]>>d[1]>>d[2]>>d[3];int s;cin>>s;
		int ans=0;
		for(int i=0;i<(1<<4);i++){ //枚举子集
			int sum=s,num=0;
			for(int j=0;j<4;j++){
				if(i>>j&1){
					sum-=c[j]*(d[j]+1);	num++;
				}
			}
			if(sum<0) continue;
			if(num&1) ans-=dp[sum]; //偶加奇减
			else ans+=dp[sum];
		}
		cout<<ans<<endl;
	}
	return 0;
}