深入理解数据库索引采用B树和B+树的原因

前面几篇关于数据库底层磁盘文件读取，数据库索引实现细节进行了深入的研究，但是没有串联起来的讲解为什么数据库索引会采用B树和B+树而不是其他的数据结构，例如平衡二叉树、链表等，因此，本文打算从数据库文件存储以及读取说起，讲解数据库索引的由来。

我们以抛出问题的形式开始讲解：

（1）数据库文件存储的方式
     数据库文件存储都是以磁盘文件存储在系统中的，这也是数据库能持久化存储数据的原因。

（2）从数据库读取数据的原理
        从数据库读取数据，先暂且不考虑从缓存中读取数据的情况，那就是从磁盘文件中读取数据的，我们知道从磁盘文件中读取数据是比较耗时的，数据库的select操作的时间，取决于执行磁盘IO的次数，因此尽量减少磁盘IO就可以显著的提升数据的查询速度。

（3）减少磁盘IO操作的影响因素
      有哪些因素可以减少磁盘IO呢，这首先得将了解一下磁盘IO与预读。

磁盘IO与预读

磁盘读取依靠的是机械运动，分为寻道时间、旋转延迟、传输时间三个部分，这三个部分耗时相加就是一次磁盘IO的时间，大概9ms左右。这个成本是访问内存的十万倍左右；正是由于磁盘IO是非常昂贵的操作，所以计算机操作系统对此做了优化：预读；每一次IO时，不仅仅把当前磁盘地址的数据加载到内存，同时也把相邻数据也加载到内存缓冲区中。因为局部预读原理说明：当访问一个地址数据的时候，与其相邻的数据很快也会被访问到。每次磁盘IO读取的数据我们称之为一页（page）。一页的大小与操作系统有关，一般为4k或者8k。这也就意味着读取一页内数据的时候，实际上发生了一次磁盘IO。

正因为有了磁盘IO预读机制，所以才有了减少磁盘IO的可能，因为一次磁盘IO操作，可以查找到物理存储中相邻的一大片数据。

以索引为B+树为例：

磁盘IO次数和索引数据结构查询的次数以及磁盘IO与预读都有关系，具体关系：磁盘IO次数 <= B+树中从根节点一直到叶子节点整个过程中查询的节点数。

一次磁盘IO操作可以取出物理存储中相邻的一大片数据，如果查询的索引数据（就是B+树中从根节点一直到叶子节点整个过程中查询的节点数）都集中在该区域，那么只需要一次磁盘IO，否则就需要多次磁盘IO

（4）基于磁盘IO预读机制，索引可以快速查询数据
   到现在才开始讲解索引了。正是基于磁盘IO预读机制的前提，数据库可以采用索引机制快速查询出数据。

（a）什么是索引

索引是帮助数据高效查询数据的一种数据结构，它包含一个表中某些列的值以及记录对应的地址，并且把这些值存储在一个数据结构中。常用的索引有B树和B+树

（b）为什么要使用索引

举个例子来说，假设我们有一个数据库student，这个表分别有三个字段：name，age，class。假设表中有2000条记录。

1、假如没有使用索引，当我们查询名为“xiaxia”的学生的时候，即调用：

select name,age,class from student where name = "xiaxia";
      此时数据库不得不在student表中对这2000条记录一条一条的进行判断name字段是否为“xiaxia”。这也就是所谓的全表扫描。

2、而当我们在student表上的name字段上创建索引时，当我们查询名为“xiaxia”的学生时：

会通过索引查找去查询名为“xiaxia”的学生，因为该索引已经按照字母顺序排列，因此要查找名为“xiaxia”的记录时会快很多，因为名字首字母为“x”的雇员都是排列在一起的。通过该索引，能获取到表中对应的记录。

（5）数据库中使用什么数据结构作为索引
     （a）链表

链表的查询速度是O（N），每次查询都得从链表头开始查询，例如上面查询“xiaxia”，如果xiaxia在1000的位置，那么需要遍历1000次才能查找到。

（b）数组

有人可能会说，查询速度肯定是数据最快呀，毕竟O（1），的确单纯就select的话，采用数组的形式是最合适的，但是采用数组会遇到如下几个问题：1、采用数组的话，其他操作如Delete、Update、Insert就不合适了；2、另外一个原因：索引是存在于磁盘中，当索引非常大的时候，达到几个G的时候，无法一次加载到内存中。

（c）平衡二叉树

二叉查找树查询的时间复杂度是O（logN），查找速度最快和比较次数最少，既然性能已经如此优秀，但为什么实现索引是使用B-Tree而不是二叉查找树，关键因素是磁盘IO的次数。

（d）B树和B+树

数据库索引采用的数据结构

（6）采用平衡二叉树和B树，数据查询的对比
      这里直接引用https://blog.csdn.net/sinat_27602945/article/details/80118362，感谢博主。

二叉树查询过程：
           我们先来看二叉树查找时磁盘IO的次：定义一个树高为4的二叉树，查找值为10：

​

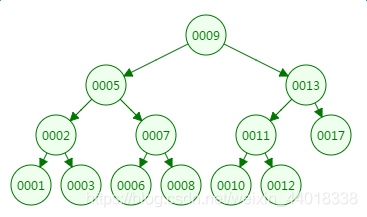
第一次磁盘IO：

​

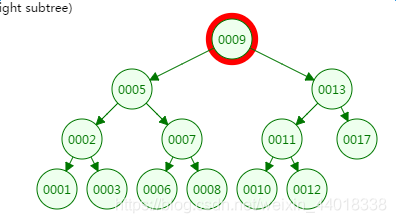
第二次磁盘IO

​

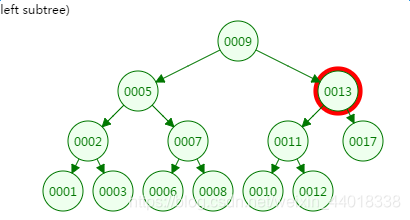
第三次磁盘IO:

​

第四次磁盘IO：

​

从二叉树的查找过程了来看，树的高度和磁盘IO的次数都是4，所以最坏的情况下磁盘IO的次数由树的高度来决定。

从前面分析情况来看，减少磁盘IO的次数就必须要压缩树的高度，让瘦高的树尽量变成矮胖的树，所以B-Tree就在这样伟大的时代背景下诞生了。

B-Tree查询过程：
 如下有一个3阶的B树，观察查找元素21的过程：

​

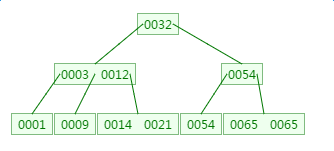
第一次磁盘IO：

​

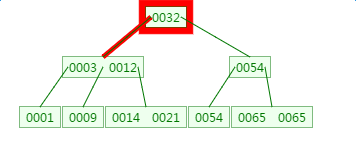
第二次磁盘IO：

​

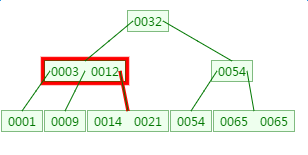
这里有一次内存比对：分别跟3与12比对

第三次磁盘IO:

​

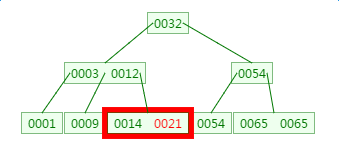
B树的查询次数少于平衡二叉树！所以基于B树以及B+树的查询次数少于平衡二叉树。

关于B+树的具体讲解，可以参照前面的博客：漫画叙述B+树和B-树，很值得看!