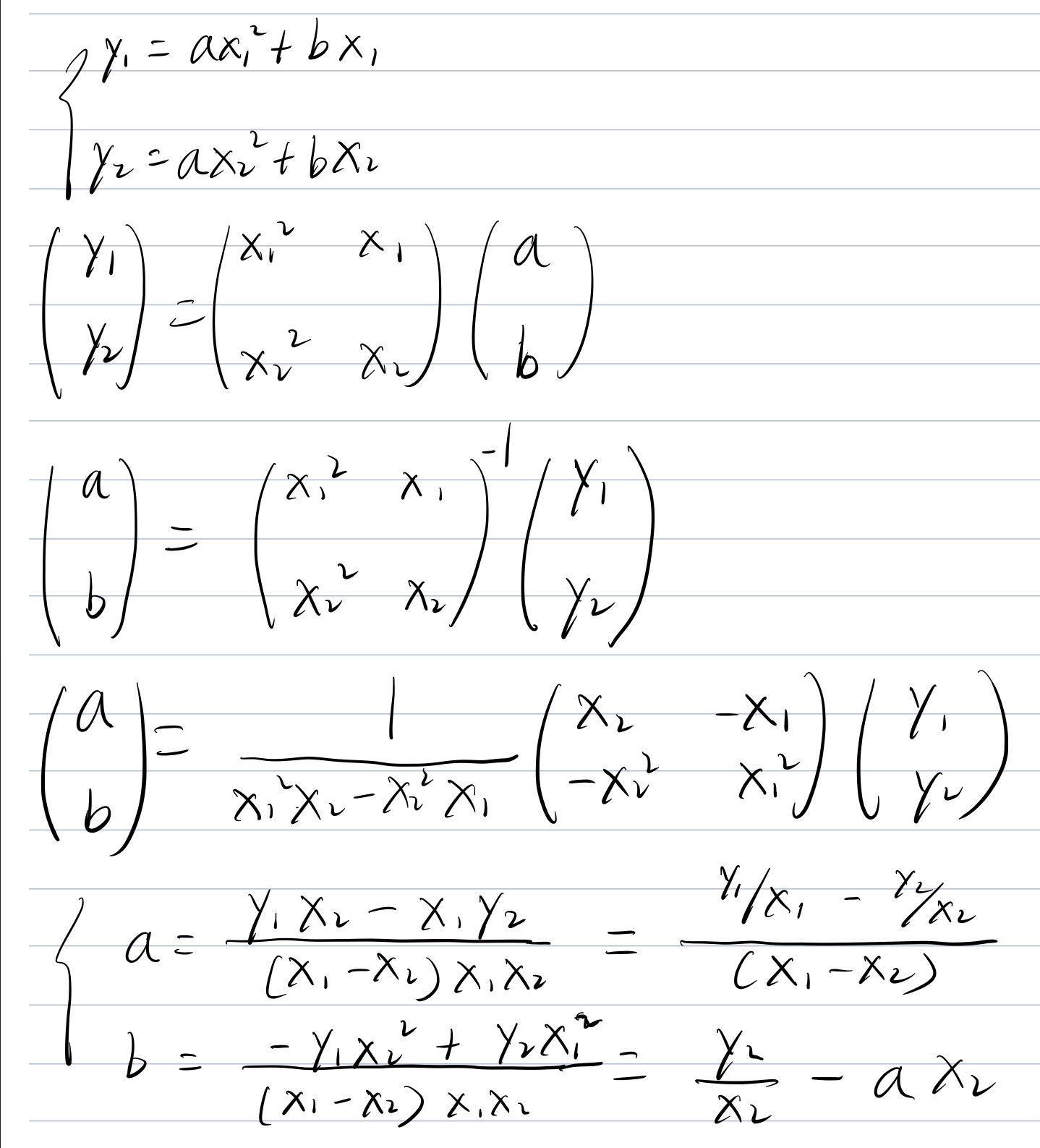luogu_2831: 愤怒的小鸟
洛谷2831:愤怒的小鸟(状压\(dp\))
题意:
- 在二维平面上给定\(n\)个点\((1\leq n\leq18)\)。
- 其中每个点用\((x_i,y_i)\)表示\((0<x_i,y_i<10)\),输入均保留两位小数。
- 求最少多少个经过原点的抛物线贯穿所有点。
输入格式:
- 第一行输入一个整数\(T\)代表有T组测试样例。
- 第二行输入两个整数\(n\)和\(m\)分别代表有多少个点和\(m\)的限制(见题意)。
- 其实这个\(m\)没什么用
- 接下来\(n\)行输入每行输入两个浮点数表示点的坐标。
输出格式:
- 输出\(T\)个整数表示答案。
思路:
这个数据范围不是爆搜就是状压。
首先题面说明必须要经过原点,所以原本三点确定抛物线,现在我们可以用两个点就能确定一条抛物线了。
所以可以用\(line(i,j)\)表示穿过\(i,j\)的抛物线所能经过所有点的集合。
再设\(f(s)\)表示在\(s\)状态下已经穿过了的点所需要的最少抛物线数。
当然,有:
- \(f(0)=0\)
- 枚举没有被穿过的点\(i,j\)
- \(f(s|line(i,j))=min(f(s|line(i,j)),f(s)+1)\)
- 考虑有些点可能只能用一条抛物线单独穿过,即他不能和其他点计算出合法抛物线。
- 所以还需要枚举未穿过的点对其单独穿过。
- \(f(s|(1<<(i-1)))=min(f(s|1<<(i-1)),f(s)+1)\)
- 最后答案为\(f((1<<n)-1)\)
需要遍历整个状态,所以有\(2^n\),同时需要枚举\(i\)和\(j\)。
总复杂度为\(O(Tn^22^n)\)带入\(n==18\)算一下发现稍微有点危险。
所以考虑优化
优化\(1:\)
- 当\(i\in S\)或者\(j\in S\)时没必要转移。(但这只是一个常数优化)
优化\(2:\)
- 对于每一个状态\(i\),我们找到他正数第一个没有被穿过的抛物线进行转移后\(break\)掉。
- 因为如果转移了第一个后面的某一个没有被穿过的点,在转移的过程中还是需要穿过第一个点。
- 所以我们每次处理第一个没被处理的点,后面的一个一个轮着转移就行了。
怎么判断一个点是不是在另外两个点确定的抛物线上?
即满足\(a,b\)的条件的时候就能判定在一条抛物线上了
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 25, INF = 0x3f3f3f3f;
int T, n, m;
int line[maxn][maxn];
int f[1<<maxn];
double x[maxn], y[maxn];
inline bool same(double x, double y){
return fabs(x - y) < 1e-6;
}
void init()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%lf%lf", &x[i], &y[i]);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
line[i][j] = 0;
//考虑ij每一种组合
for(int i = 1; i <= n-1; i++)
for(int j = i + 1; j <= n; j++)
{
if(same(x[i], x[j])) continue; //如果他们在同一列
double aa = (y[j]/x[j] - y[i]/x[i]) / (x[j]-x[i]);
if(aa >= 0) continue;
double bb = y[i]/x[i] - aa*x[i];
for(int k = 1; k <= n; k++)
if(same(aa*x[k]+bb, y[k]/x[k])) //如果他在这条抛物线上
line[i][j] |= (1<<(k-1));
}
for(int i = 0; i <= (1<<n)-1; i++) f[i] = INF; f[0] = 0;
}
int main()
{
scanf("%d", &T);
while(T--)
{
init();
for(int i = 0; i <= (1<<n)-1; i++)
{
for(int j = 1; j <= n; j++)
if(!(i&(1<<(j-1)))) //如果这里有一个没有穿过的点
{
for(int k = j; k <= n; k++) //前面的已经串好了
{
if(j == k)
f[i|(1<<(j-1))] = min(f[i|(1<<(j-1))], f[i]+1);
if(same(x[j], x[k])) continue;
//用已有的线好还是再多一条线好
f[i|line[j][k]] = min(f[i|line[j][k]], f[i]+1);
}
break;
}
}
//输出答案
printf("%d\n", f[(1<<n)-1]);
}
return 0;
}
luogu_2831: 愤怒的小鸟的更多相关文章
- [NOIP2016]愤怒的小鸟 D2 T3 状压DP
[NOIP2016]愤怒的小鸟 D2 T3 Description Kiana最近沉迷于一款神奇的游戏无法自拔. 简单来说,这款游戏是在一个平面上进行的. 有一架弹弓位于(0,0)处,每次Kiana可 ...
- 基于html5实现的愤怒的小鸟网页游戏
之前给大家分享一款基于html5 canvas和js实现的水果忍者网页版,今天给大家分享一款基于html5实现的愤怒的小鸟网页游戏.这款游戏适用浏览器:360.FireFox.Chrome.Safar ...
- [luogu2831][noip d2t3]愤怒的小鸟_状压dp
愤怒的小鸟 noip-d2t3 luogu-2831 题目大意:给你n个点,问最少需要多少条经过原点的抛物线将其覆盖. 注释:1<=点数<=18,1<=数据组数<=30.且规定 ...
- 洛谷P2831 愤怒的小鸟 + 篮球比赛1 2
这三道题一起做,有一点心得吧. 愤怒的小鸟,一眼看上去是爆搜,但是实现起来有困难(我打了0分出来). 还有一种解法是状压DP. 抛物线一共只有那么多条,我们枚举抛物线(枚举两个点),这样就能够预处理出 ...
- Unity3D笔记 愤怒的小鸟<二> 实现Play界面
创建Play界面.能个把各个图片组合成一个场景,场景组成后背景能够不停的滚动,当鼠标单击时显示图片手型鼠标 一.GUI Texture 1.创建背景.地面.树木.草 ,这里注意Z轴的排序,一层一层则第 ...
- Unity3D笔记 愤怒的小鸟<一>场景切换
新建3个场景,场景1 Start 十秒后自动切换到场景2 Splash,场景2在二秒后自动切换到场景3 Selection 一.场景一Start 二.场景2 Splash 三.场景3 Selectio ...
- Unity3D游戏-愤怒的小鸟游戏源码和教程(二)
Unity愤怒的小鸟游戏教程(二) 本文提供全流程,中文翻译.Chinar坚持将简单的生活方式,带给世人!(拥有更好的阅读体验 -- 高分辨率用户请根据需求调整网页缩放比例) AngryEva游戏效果 ...
- Unity3D游戏-愤怒的小鸟游戏源码和教程(一)
Unity愤怒的小鸟游戏教程 本文提供全流程,中文翻译.Chinar坚持将简单的生活方式,带给世人!(拥有更好的阅读体验 -- 高分辨率用户请根据需求调整网页缩放比例) AngryEva游戏效果: 1 ...
- 【NOIP2016提高组】 Day2 T3 愤怒的小鸟
题目传送门:https://www.luogu.org/problemnew/show/P2831 说个题外话:NOIP2014也有一道题叫做愤怒的小鸟. 这题自测时算错了eps,导致被卡了精度,从1 ...
随机推荐
- java数字前面补充0公共方法
- k8s-架构中各个组件介绍
参考链接:https://github.com/opsnull/follow-me-install-kubernetes-cluster kubernetes 概述 1.kubernetes 是什么 ...
- ES集群7.3.0设置快照,存储库进行索引备份和恢复等
说明:三台ES节点组成ES集群,一台kibana主机,版本均是7.3.0,白金试用版 官方地址:https://www.elastic.co/guide/en/elasticsearch/refere ...
- Wireshark教程之一:认识Wireshark界面
1.下载与安装 官网地址:https://www.wireshark.org/ 官网下载地址:https://www.wireshark.org/#download 本文以windows环境为例来说明 ...
- 服务发现对比:Zookeeper vs etcd vs Consul
我们拥有的服务越多,如果我们使用预定义的端口,就会发生冲突的可能性越大.毕竟,在同一端口上不能监听两个服务.管理一百个服务所使用的所有端口的紧密列表本身就是一项挑战.将那些服务所需的数据库添加到该列表 ...
- java 泛型和object比较
引言 我们使用object和泛型做形参,都是为了让这个方法能接收更多类型的对象,让程序变得更健壮,代码复用率更高.当我们回看自己写的代码时会发现,好像使用泛型的地方使用object也可以,使用obje ...
- Socker编程之UDP
一:socket简介 1. 不同电脑上的进程之间如何通信 首要解决的问题是如何唯一标识一个进程,否则通信无从谈起! 在1台电脑上可以通过进程号(PID)来唯一标识一个进程,但是在网络中这是行不通的. ...
- [echart] webpack中安装和使用
安装echart npm install echarts --save 全量引入 可以直接在项目代码中 require('echarts') 得到 ECharts. 官方示例 var echarts ...
- vue路由切换时内容组件的滚动条回到顶部
在使用vue的时候会出现切换路由的时候滚动条保持在原来的位置,要切换路由的时候滚动条回到顶部才有更好的用户体验 1.当页面整体都要滚动到顶部的情况 router.afterEach(() => ...
- 渐进增强(progressive enhancement)、优雅降级(graceful degradation)
渐进增强 progressive enhancement: 针对低版本浏览器进行构建页面,保证最基本的功能,然后再针对高级浏览器进行效果.交互等改进和追加功能达到更好的用户体验. 优雅降级 grace ...