Codeforces 1239B. The World Is Just a Programming Task (Hard Version)

传送门

这一题好妙啊

首先把括号序列转化成平面直角坐标系 $xOy$ 上的折线，初始时折线从坐标系原点 $(0,0)$ 出发

如果第 $i$ 个位置是 '(' 那么折线就往上走一步（$y+1$），否则往下走一步 （$y-1$）

这条折线有很多有用的性质

$1.$如果某个时刻折线的纵坐标为负数了，那么说明这个括号序列一定是不合法的

证明也挺好理解的，变成负数说明没有足够的 '(' 和 ')' 匹配了，显然不合法

$2.$如果最终位置 $n$ 的折线 $y$ 坐标不为 $0$ ，那么一定不合法，因为这样说明 '(' 和 ')' 数量不相等

$3.$如果以上两条都不满足，那么括号序列合法，证明应该是挺显然的吧，即任何位置的 ')' 都能得到匹配并且最后全部匹配完毕

并且可以发现，在保证最终位置折线 $y$ 坐标为 $0$ 的情况下，这个括号序列的不同循环移位的合法序列数即为 这些到达最小值的位置数

设这些位置的序列为 $p$

对初始序列进行循环移位 $p_1,p_2,p_3...$ 后括号序列是合法的，并且其他的循环移位后都不合法

证明首先设 $a_1,a_2,a_3...a_n$ 是初始时的括号序列

那么对于循环移位 $p$ ，相当于把序列 $a$ 变成 $a_{p+1}a_{p+2}...a_{n}a_{1}a_{2}a_{3}...a_{p}$

那么假设原本折线在位置 $p$ 时的 $y$ 的值为 $t$ （显然 $t<=0$）

那么对于 $(p,n]$ 的这一段折线，显然它的形状不会变，并且 $y$ 坐标同时增加 $-t$

这个挺好理解的吧，首先 $p$ 位置的 $y$ 变成 $0$ ，后面的就和 $p$ 位置一起变了

然后 $[0,p]$ 这一段折线再接到原本位置 $n$ 的后面（显然这一段折线也增加了 $-t$），看图理解吧：

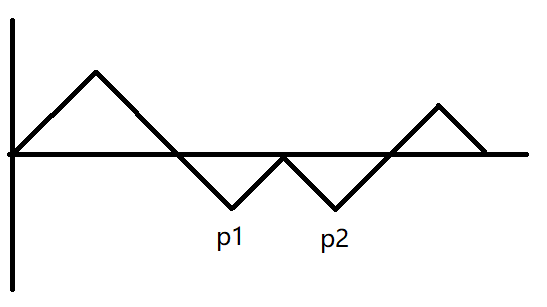
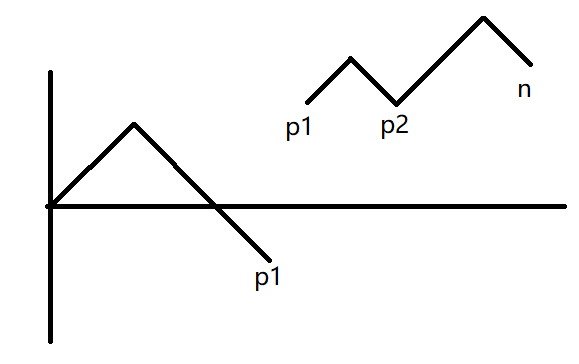
上图展示了循环移位 $p1$ 后折线的变化

由于 $t$ 是初始折线最小的纵坐标，那么循环移位后就不存在任何位置的 $y$ 小于 $0$

由上图你会发现所有的 $y$ 都增加了 $-t$，又因为折线的形状不变所以所有位置的 $y$ 都大于等于 $0$

然后又因为最终位置的 $y$ 一定为 $0$（由于初始时位置 $n$ 的 $y$ 为 $0$，那么左右括号数量永远相等，不管怎么循环移位最终位置都是 $y=0$）

那么说明这一段循环移位后括号序列一定是合法的（由之前证明的第 $3$ 条可得）

现在只剩下证明其他的循环移位都不合法即可，其实十分显然，因为从其他位置循环移位后坐标增加量不到 $-t$

那么对于初始为 $t$ 的位置增加后还是小于 $0$，还是不合法

所以我们经历了千辛万苦终于证明了官方题解里一句话的东西：

It can easily be shown that the answer to the question of the number of cyclic shifts being correct bracket sequence is the number of times how much minimum balance is achieved in the array of prefix balances.

如果此时你理解了循环移位对于折线的变化，那么就很容易知道交换两个位置对折线的变化

如果交换 ')' 和 '(' ，会导致一段区间的 $y$ 加 $2$ ，那么对答案毫无意义，只会让答案变小

所以只能交换 '(' 和 ')' ，那么会导致区间的 $y$ 减 $2$，如果你改变的区间跨过了某个 $p_i$ （$p_i$ 的定义同上）

那么只会让答案更小，因为此时只有跨过的 $p$ 会产生贡献，还不如原本更多的 $p$

为了方便，现在让我们把折线用循环移位变成任意时刻都大于等于 $0$ 的情况（显然对任意一个 $p_i$ 进行循环移位 $p_i$ 即可）

此时所有初始位置为 $p$ 的位置的 $y$ 均为 $0$，设此时 $y$ 为 $0$ 的位置为新的序列 $p$

因为之前证明的，交换只能在区间 $(p_i,p_{i+1})$ 进行，如果我们把 $p_{i}+1$ （显然是 '('）和 $p_{i+1}$ 交换（显然是 ')'）

那么区间内所有 $y$ 值为 $1$ 的位置因为减 $2$ 就变成了最小的位置（区间内不存在 $y=0$ 的位置），那么交换以后序列的答案即为初始这一段区间内 $1$ 的个数

为了答案最大我们显然只要考虑 $(p_i,p_{i+1})$ 区间内 $1$ 的个数

然后考虑把 $y=2$ 的位置通过减 $2$ 变成 $0$ ，那么答案就是初始时的答案加上区间内 $y=2$ 的贡献（注意此时区间内不能有 $0,1$）

我们同样可以找到这些位置，然后操作一下看看答案是多少即可，实现起来还是有点细节的

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=3e5+;
int n,cnt,sl,sr,sum[N];
char s[N],tmp[N];
int main()
{
    n=read(); scanf("%s",s+);
    int pos=,now=,mi=;
    for(int i=;i<=n;i++)
    {
        now+=s[i]=='(' ?  : -;
        if(now<mi) mi=now,pos=i;
    }
    if(now!=) { printf("0\n1 1\n"); return ; }
    for(int i=;i<=n;i++) tmp[i]=s[ (pos+i-)%n+ ];
    vector <int> V; V.push_back();
    for(int i=;i<=n;i++)
    {
        s[i]=tmp[i]; sum[i]=sum[i-] + (s[i]=='(' ?  : -);
        if(!sum[i]) cnt++,V.push_back(i);
    }
    int ans=cnt,L=,R=,len=V.size();
    for(int i=;i<len;i++)
    {
        int l=V[i-]+,r=V[i],t=;
        for(int j=l;j<=r;j++) t+=sum[j]==;
        if(t>ans) ans=t,L=l,R=r;
    }
    V.clear(); for(int i=;i<=n;i++) if(sum[i]==) V.push_back(i);
    len=V.size();
    for(int i=;i<len;i++)
    {
        int l=V[i-]+,r=V[i],t=cnt;
        if(sum[l]==) continue;//如果sum[l]不为0,那么sum[l]一定为2,那么下一个sum为1的位置一定为r,即[l,r)之间不存在sum为0或1的位置
        for(int j=l;j<=r;j++) t+=sum[j]==;
        if(t>ans) ans=t,L=l,R=r;
    }
    printf("%d\n%d %d\n",ans,(L+pos-)%n+,(R+pos-)%n+);
    return ;
}