LDA算法 (主题模型算法) 学习笔记
转载请注明出处: http://www.cnblogs.com/gufeiyang
随着互联网的发展,文本分析越来越受到重视。由于文本格式的复杂性,人们往往很难直接利用文本进行分析。因此一些将文本数值化的方法就出现了。LDA就是其中一种很NB的方法。 LDA有着很完美的理论支撑,而且有着维度小等一系列优点。本文对LDA算法进行介绍,欢迎批评指正。
本文目录:
1、Gamma函数
2、Dirichlet分布
3、LDA文本建模
4、吉普斯抽样概率公式推导
5、使用LDA
1、Gamma函数
T(x)= ∫ tx-1 e-tdt T(x+1) = xT(x)
若x为整数,则有 T(n) = (n-1)!
2、Dirichlet分布
这里抛出两个问题:
问题1: (1) X1, X2......Xn 服从Uniform(0,1)
(2) 排序后的顺序统计量为X(1), X(2), X(3)......X(n)
(3) 问X(k1)和X(k1+k2)的联合分布式什么
把整个概率区间分成[0,X1) , [X1, X1+Δ), [X1+Δ, X1+X2), [X1+X2, X1+X2+Δ), [X1+X2+Δ,1]
X(k1) 在区间[X1, X1+Δ), X(k1+k2) 在区间[X1+X2, X1+X2+Δ)。 我们另X3 = 1-X1-X2.
则,
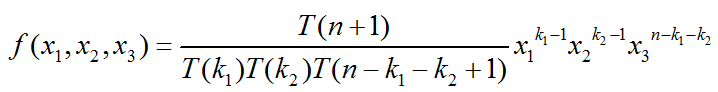
即Dir(x1, x2, x3| k1, k2, n-k1-k2+1)
问题2: (1) X1, X2......Xn 服从Uniform(0,1), 排序后的顺序统计量为X(1), X(2), X(3)......X(n)
(2) 令p1 = [0, X(k1)], p2 = [X(k1), X(k1+k2)], p3 = 1-p1-p2
(3) 另外给出新的信息, Y1, Y2.....Ym服从Uniform(0, 1), Yi落到[0,X(k1)], [X(k1), X(k1+k2)], [X(k1+k2), 1]的数目分别是m1, m2, m3
(4) 问后验概率 p(p1,p2,p3|Y1,Y2,....Ym)的分布。
其实这个问题和问题1很像,只是在同样的范围内多了一些点而已。 因此这个概率分布为 Dir(x1,x2,x3| k1+m1, k2+m2, n-k1-k2+1+m3)。
我们发现这么一个规律 Dir(p|k) + multCount(m) = Dir(p|k+m)。 即狄利克雷分布是多项分布的共轭分布。
狄利克雷分布有这么一个性质:如果 则,
则,

3、 LDA文本建模
首先我们想一篇文章是如何形成的:作者在写一篇文章的时候首先会想这个文章需要包含什么主题呢。比如在写武侠小说的时候,首先会想小说里边需要包含武侠、爱情、亲情、搞笑四个主题。并且给这四个主题分配一定的比例(如武侠0.4,爱情0.3,亲情0.2,搞笑0.1)。每个主题会包含一些word,不同word的概率也是不一样的。 因此我们上帝在生成一篇文章的时候流程是这个样子的:
(1)上帝有两个坛子的骰子,第一个坛子装的是doc-topic骰子,第二个坛子装的是topic-wod骰子。
(2)上帝随机的从二个坛子中独立抽取了k个topic-doc骰子,编号1-K。
(3)每次生成一篇新的文档前,上帝先从第一个坛子中随机抽取一个doc-topic骰子,然后重复如下过程生成文档中的词。
<1>、投掷这个doc-topic骰子,得到一个topic的编号z。
<2>、选择K个topic-word骰子中编号为z的的那个,投掷这个骰子, 于是就得到了这个词。
假设语料库中有M篇文章, 所有的word和对应的topic如下表示:
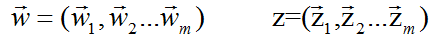
我们可以用下图来解释这个过程:

一共两个物理过程:
第一个过程:  ,这个过程分两个阶段。第一个阶段是上帝在生成一篇文档之前,先抽出一个主题分布的骰子
,这个过程分两个阶段。第一个阶段是上帝在生成一篇文档之前,先抽出一个主题分布的骰子 ,这个分布选择了狄利克雷分布(狄利克雷分布是多项分布的共轭分布)。 第二个阶段根据
,这个分布选择了狄利克雷分布(狄利克雷分布是多项分布的共轭分布)。 第二个阶段根据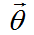 来抽样得到每个单词的topic。这是一个多项分布。 整个过程是符合狄利克雷分布的。
来抽样得到每个单词的topic。这是一个多项分布。 整个过程是符合狄利克雷分布的。
第二个过程: ,这个过程也分两个阶段。第一个阶段是对每个主题,生成word对应的概率,即选取的骰子
,这个过程也分两个阶段。第一个阶段是对每个主题,生成word对应的概率,即选取的骰子 ,这个分布也是选择了狄利克雷分布。 第二个阶段是根据
,这个分布也是选择了狄利克雷分布。 第二个阶段是根据 ,对于确定的主题选择对应的word,这是一个多项分布。因此,整个过程是狄利克雷分布。
,对于确定的主题选择对应的word,这是一个多项分布。因此,整个过程是狄利克雷分布。
4、吉普斯抽样概率公式推导
LDA的全概率公式为:  。 由于
。 由于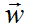 是观测到的已知数据,只有
是观测到的已知数据,只有 是隐含的变量,所以我们需要关注的分布为:
是隐含的变量,所以我们需要关注的分布为: 。 我们利用Gibbs Sampling进行抽样。 我们要求的某个位置i(m,n)对应的条件分布为
。 我们利用Gibbs Sampling进行抽样。 我们要求的某个位置i(m,n)对应的条件分布为 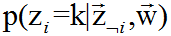 。
。
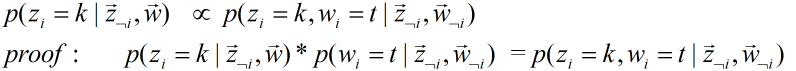
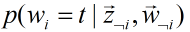 是一个定值,因此原公式成立。
是一个定值,因此原公式成立。
下边是公式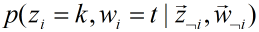 的推导:
的推导:
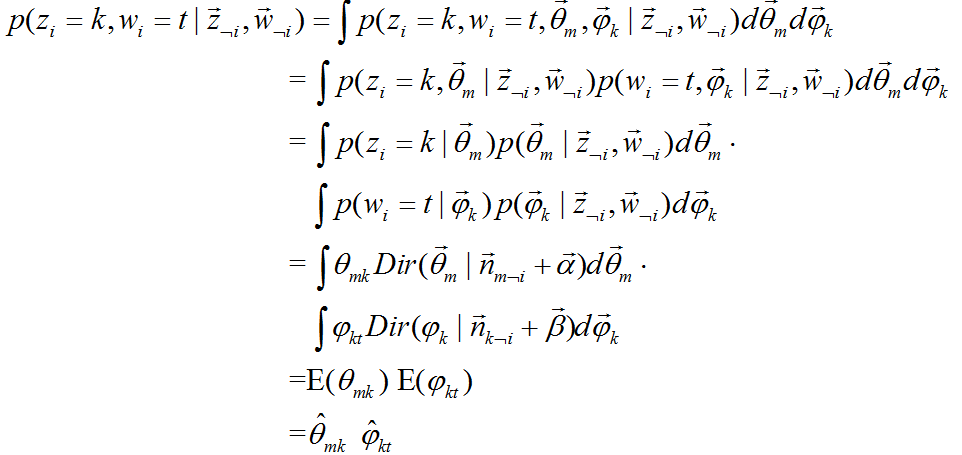
又由于根据狄利克雷分布的特性:
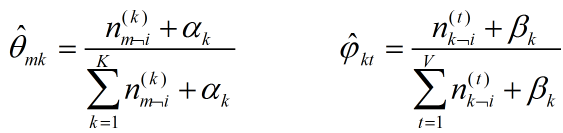

抽样的时候,首先随机给每个单词一个主题,然后用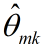 和
和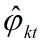 进行Gibbs抽样,抽样后更新这两个值,一直迭代到收敛(EM过程)。
进行Gibbs抽样,抽样后更新这两个值,一直迭代到收敛(EM过程)。
至此抽样就结束了。
5、使用LDA
抽样结束后,我们可以统计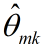 和
和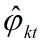 来得到
来得到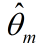 和
和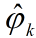 。
。
对于LDA我们的目标有两个:
(1)得到文章库中每篇文章的主题分布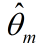
(2)对于一篇新来的文章,能得到它的主题分布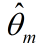 。
。
第一个目标很容易就能达到。下面主要介绍如果计算 一篇新文章的主题分布。这里我们假设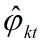 是不会变化的。因此对于一篇新文章到来之后,我们直接用Gibbs Sampling得到新文章的
是不会变化的。因此对于一篇新文章到来之后,我们直接用Gibbs Sampling得到新文章的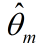 就好了。 具体抽样过程同上。
就好了。 具体抽样过程同上。
由于工程上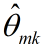 对于计算新的文章没有作用,因此往往只会保存
对于计算新的文章没有作用,因此往往只会保存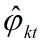 。
。
参考资料:
《LDA数学八卦》 Rickjin著
python LDA package:
http://pythonhosted.org/lda/index.html
LDA算法 (主题模型算法) 学习笔记的更多相关文章
- LDA(主题模型算法)
LDA整体流程 先定义一些字母的含义: 文档集合D,topic集合T D中每个文档d看作一个单词序列< w1,w2,...,wn >,wi表示第i个单词,设d有n个单词.(LDA里面称之为 ...
- Spark:聚类算法之LDA主题模型算法
http://blog.csdn.net/pipisorry/article/details/52912179 Spark上实现LDA原理 LDA主题模型算法 [主题模型TopicModel:隐含狄利 ...
- [综] Latent Dirichlet Allocation(LDA)主题模型算法
多项分布 http://szjc.math168.com/book/ebookdetail.aspx?cateid=1&§ionid=983 二项分布和多项分布 http:// ...
- 机器学习实战(Machine Learning in Action)学习笔记————06.k-均值聚类算法(kMeans)学习笔记
机器学习实战(Machine Learning in Action)学习笔记————06.k-均值聚类算法(kMeans)学习笔记 关键字:k-均值.kMeans.聚类.非监督学习作者:米仓山下时间: ...
- Spark机器学习(8):LDA主题模型算法
1. LDA基础知识 LDA(Latent Dirichlet Allocation)是一种主题模型.LDA一个三层贝叶斯概率模型,包含词.主题和文档三层结构. LDA是一个生成模型,可以用来生成一篇 ...
- RSA算法、SSL协议学习笔记
最近学习计算机网络,涉及到SSL协议,我想起了去年密码学课程讲过的非对称加密RSA算法,结合阮老师的博客,写写学习笔记,这里再回忆一下. RSA算法 RSA算法是一种非对称密码算法,所谓非对称,就是指 ...
- LDA概率主题模型
目录 LDA 主题模型 几个重要分布 模型 Unigram model Mixture of unigrams model PLSA模型 LDA 怎么确定LDA的topic个数? 如何用主题模型解决推 ...
- TF-IDF与主题模型 - NLP学习(3-2)
分词(Tokenization) - NLP学习(1) N-grams模型.停顿词(stopwords)和标准化处理 - NLP学习(2) 文本向量化及词袋模型 - NLP学习(3-1) 在上一篇博文 ...
- LDA(Latent Dirichlet Allocation)主题模型算法
原文 LDA整体流程 先定义一些字母的含义: 文档集合D,topic集合T D中每个文档d看作一个单词序列< w1,w2,...,wn >,wi表示第i个单词,设d有n个单词.(LDA里面 ...
随机推荐
- layui.js源码分析
/*! @Title: Layui @Description:经典模块化前端框架 @Site: www.layui.com @Author: 贤心 @License:MIT */ ;!functi ...
- C++中头文件与源文件的作用详解
一.C++ 编译模式 通常,在一个 C++ 程序中,只包含两类文件―― .cpp 文件和 .h 文件.其中,.cpp 文件被称作 C++ 源文件,里面放的都是 C++ 的源代码:而 .h 文件则被称作 ...
- Windows环境下大数据处理的构想(一)
为什么不呢?我们有了RPC/RMI和MAP,为什么不能在windows环境下处理大数据呢?windows是迄今为止最普及的操作系统,据市调公司NetMarketShare最新(2019年5月)统计数据 ...
- Jupyter Notebook环境安装
Jupyter Notebook环境安装 一.什么是jupyter Notebook 1.简介 Jupyter Notebook 是基于网页的用于交互计算机的应用程序器可被应用程序. 能让用户将说明文 ...
- PyCharm-安装&调试
windows安装pycharm 和python的链接: PyCharm:http://www.jetbrains.com/pycharm/ Python:https://www.python.org ...
- 关于在centos下安装python3.7.0以上版本时报错ModuleNotFoundError: No module named '_ctypes'的解决办法
3.7版本需要一个新的包libffi-devel,安装此包之后再次进行编译安装即可. #yum install libffi-devel -y#make install若在安装前移除了/usr/bin ...
- mybatis中如何将多个表的查询结果,放入结果集中返回
1.首先需要将resultMap进行改造,为了避免对其他sql的影响建议另外定义一个resultMapExtral,避免id相同, 2.然后在resultMapExtral中添加其它表的字段,若多个表 ...
- IDEA实用教程(七)—— IDEA的断点调试
IDEA实用教程(七)-- IDEA的断点调试 23/100 发布文章 qq_41684621 六. IDEA的断点调试 打断点 在行号的右侧点击鼠标左键,出现红色圆形图标,说明已经被打上断点 Deb ...
- Spring4- 04-Spring简易整合Mybatis -导入jar包/ 正常编写pojo/ 编写spring 配置文件
笔记要点&出错分析与总结 POJO(Plain Ordinary Java Object)简单的Java对象,实际就是普通JavaBeans,工程组织 (AirportService为机场 ...
- robot framework 笔记(一)
背景: 平时使用rf时会用到一些方法,长时间不用就会忘记,本文用来记录当做自己的小笔记 内容持续更新中········ 一.robot framework 大小写转换 1.转换小写: ${low} E ...
