【洛谷P3756】[CQOI2017]老C的方块（最小割）

洛谷

题意：

给出一个网格图类似于这样：

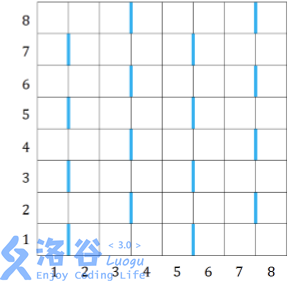
现在给出一个\(n*m\)大小的网格，之后会给出一些点，若某些点相连形成了如下的几个图案，那么就是不好的。

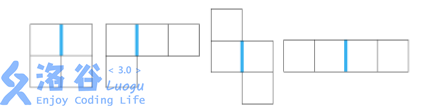
现在可以删去一些点，但删除每个点都有一些代价，问最终不出现上述图案的最小代价为多少。

思路：

初一看这图是什么乱七八糟的，但仔细观察能够发现它们的共性：对于蓝色的边两旁的格子，我们称为灰点；若有两个灰点相连，并且它们各自至少还连接了一个点，那么就是不合法的图案。

同时观察网格奇偶性，之后对网格奇偶染色。

然后初步思路为：源点连向所有白点，容量为白点权值；黑点向汇点连边，容量也为权值；然后中间为两两相连的灰点，权值为两者最小值。之后求个最小割就行了（相当于不存在一条白-灰-灰-黑的路径）。

但是这还有连边的细节需要分情况讨论一下，假设我们固定白点为起点，那么在不同行，灰点间的连边是不同的。

详见代码吧：

#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
//#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << '\n'; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
  #define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 5e5 + 5;

int c, r, n;
int x[N], y[N], w[N], col[N];
#define INF 0x3f3f3f3f
template <class T>
struct Dinic{
    struct Edge{
        int v, next;
        T flow;
        Edge(){}
        Edge(int v, int next, T flow) : v(v), next(next), flow(flow) {}
    }e[N << 1];
    int head[N], tot;
    int dep[N];
    void init() {
        memset(head, -1, sizeof(head)); tot = 0;
    }
    void adde(int u, int v, T w, T rw = 0) {
        e[tot] = Edge(v, head[u], w);
        head[u] = tot++;
        e[tot] = Edge(u, head[v], rw);
        head[v] = tot++;
    }
    bool BFS(int _S, int _T) {
        memset(dep, 0, sizeof(dep));
        queue <int> q; q.push(_S); dep[_S] = 1;
        while(!q.empty()) {
            int u = q.front(); q.pop();
            for(int i = head[u]; ~i; i = e[i].next) {
                int v = e[i].v;
                if(!dep[v] && e[i].flow > 0) {
                    dep[v] = dep[u] + 1;
                    q.push(v);
                }
            }
        }
        return dep[_T] != 0;
    }
    T dfs(int _S, int _T, T a) {
        T flow = 0, f;
        if(_S == _T || a == 0) return a;
        for(int i = head[_S]; ~i; i = e[i].next) {
            int v = e[i].v;
            if(dep[v] != dep[_S] + 1) continue;
            f = dfs(v, _T, min(a, e[i].flow));
            if(f) {
                e[i].flow -= f;
                e[i ^ 1].flow += f;
                flow += f;
                a -= f;
                if(a == 0) break;
            }
        }
        if(!flow) dep[_S] = -1;
        return flow;
    }
    T dinic(int _S, int _T) {
        T max_flow = 0;
        while(BFS(_S, _T)) max_flow += dfs(_S, _T, INF);
        return max_flow;
    }
};
Dinic <int> solver;
map <int , int> mp[N];
const int dx[] = {1, -1, 0, 0};
const int dy[] = {0, 0, 1, -1};

void run() {
    for(int i = 1; i <= n; i++) {
        cin >> x[i] >> y[i] >> w[i];
        mp[x[i]][y[i]] = i;
        if(y[i] % 2 == 0) {
            if(x[i] % 4 == 0 || x[i] % 4 == 3) col[i] = 2;
            else if((x[i] + y[i]) & 1) col[i] = 1;
            else col[i] = 0;
        } else {
            if(x[i] % 4 == 1 || x[i] % 4 == 2) col[i] = 2;
            else if((x[i] + y[i]) & 1) col[i] = 1;
            else col[i] = 0;
        }
    }
    solver.init();
    dbg(mp[1][1]);
    int s = 0, t = n + 1;
    for(int i = 1; i <= n; i++) {
        if(col[i] == 1) solver.adde(s, i, w[i]);
    }
    for(int i = 1; i <= n; i++) {
        if(col[i] == 0) solver.adde(i, t, w[i]);
    }
    for(int i = 1; i <= n; i++) {
        if(col[i] == 2) continue;
        for(int j = 0; j < 4; j++) {
            int curx = x[i] + dx[j], cury = y[i] + dy[j];
            int id = mp[curx][cury];
            if(id > 0 && col[id] == 2) {
                if(col[i] == 0) {
                    solver.adde(id, i, INF);
                }
                else {
                    solver.adde(i, id, INF);
                }
            }
        }
    }
    for(int i = 1; i <= n; i++) {
        if(col[i] != 2) continue;
        int curx, cury;
        if(y[i] % 2) {
            curx = x[i] + 1, cury = y[i];
        } else {
            curx = x[i] - 1, cury = y[i];
        }
        int id = mp[curx][cury];
        if(id > 0 && col[id] == 2) {
            solver.adde(i, id, min(w[id], w[i]));
        }
    }
    int ans = solver.dinic(0, t);
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    while(cin >> c >> r >> n) run();
    return 0;
}