MongoDB 之 "$" 的奇妙用法 MongoDB - 5
在MongoDB中有一个非常神奇的符号 "$"
"$" 在 update 中 加上关键字 就 变成了 修改器
其实 "$" 字符 独立出现也是有意义的 , 我起名叫做代指符
首先看个例子: 还是这个Collection

现在把 "score": 100 的 test_list 里面的 2 改为 9

{$set :{"test_list." : 9}} 这样就是对应 Array 中的下标进行修改了 "test_list.下标"
问题来了 如果 是 一个很长很长很长的 Array 你要查找其中一个值,把这个值修改一下怎么整呢?

神奇不神奇?
$ 字符 在语句中代表了什么呢? 下标,位置
解释一下: 首先我们查询一下db.Oldboy.findOne({"score":100,"test_list":3}) 返回 给我们满足条件的数据对吧
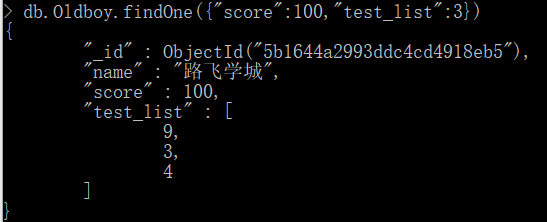
那么 如果 我们 使用 update的话, 满足条件的数据下标位置就会传递到 $ 字符中,在我们更新操作的时候就相当于 对这个位置 的元素进行操作
MongoDB 之 "$" 的奇妙用法 MongoDB - 5的更多相关文章
- 5,MongoDB 之 "$" 的奇妙用法
在MongoDB中有一个非常神奇的符号 "$" "$" 在 update 中 加上关键字 就 变成了 修改器 其实 "$" 字符 独立出现 ...
- python 全栈开发,Day124(MongoDB初识,增删改查操作,数据类型,$关键字以及$修改器,"$"的奇妙用法,Array Object 的特殊操作,选取跳过排序,客户端操作)
一.MongoDB初识 什么是MongoDB MongoDB 是一个基于分布式文件存储的数据库.由 C++ 语言编写.旨在为 WEB 应用提供可扩展的高性能数据存储解决方案. MongoDB 是一个介 ...
- mongodb学习(2)--- nodeJS与MongoDB的交互(使用mongodb/node-mongodb-native)
转载:http://www.cnblogs.com/zhongweiv/p/node_mongodb.html 目录 简介 MongoDB安装(windows) MongoDB基本语法和操作入门(mo ...
- NoSql非关系型数据库之MongoDB应用(二):安装MongoDB可视化工具
业精于勤,荒于嬉:行成于思,毁于随. 我们上次说到NoSql非关系型数据库之MongoDB应用(一):安装MongoDB服务 这次我们介绍安装 NoSQL Manager for MongoDB 可 ...
- MongoDB的安装与设置MongoDB服务
Mongo DB 是目前在IT行业非常流行的一种非关系型数据库(NoSql),其灵活的数据存储方式备受当前IT从业人员的青睐.Mongo DB很好的实现了面向对象的思想(OO思想),在Mongo DB ...
- MongoDB学习笔记(1):MongoDB简介
1. MongoDB的特点: (1) 易于使用 MongoDB是一个面向文档的数据库,非关系型数据库.通过在文档中嵌入式文档和数据,面向对象的方法能够仅使用一条记录来表现复杂的层次关系.文档的键和值不 ...
- Mongodb Manual阅读笔记:MongoDB教程
Mongodb教程的说明,可以当手册用 Getting Started Install MongoDB on Linux Systems Install MongoDB on Red Hat Ente ...
- MongoDB笔记(一)MongoDB概述和安装
概述 关键词:关系数据库.非关系数据库 关系数据库: 关系数据库,是建立在关系数据库模型基础上的数据库,借助于集合代数等概念和方法来处理数据库中的数据.目前主流的关系数据库有oracle.SQL.ac ...
- Linux平台安装MongoDB及使用Docker安装MongoDB
一.Linux平台安装MongoDB MongoDB 提供了 linux 各发行版本 64 位的安装包,你可以在官网下载安装包. 下载地址:https://www.mongodb.com/downlo ...
随机推荐
- hadoop-lzo 安装配置
在hive中要想使用lzo的格式,需要配置安装好lzo工具并且在hadoop的core-site.xml与mapred-site.xml中配置相应的配置 一.编译安装lzo与lzop 在 ...
- Notes of Daily Scrum Meeting(12.18)
前期落下的进度我们会在周六周日赶一下,在编译课程设计中期测试之后集中处理项目中的问题. 今天的任务总结如下: 团队成员 今日团队工作 陈少杰 调试后端连接的部分,寻找bug 王迪 测试搜索功能,修改b ...
- 第二阶段站立会议alpha版总结
一.会议过程 在完成第二次冲刺后,Alpha版本最终发布,我们对校园二手交易平台开发过程及产品存在的问题进行了激烈讨论.进行了我们的团队总结会议,会议中每个人先发表了个人对Alpha版开发过程中存在的 ...
- ELK 性能(2) — 如何在大业务量下保持 Elasticsearch 集群的稳定
ELK 性能(2) - 如何在大业务量下保持 Elasticsearch 集群的稳定 介绍 如何在大业务量下保持 Elasticsearch 集群的稳定? 内容 当我们使用 Elasticsearch ...
- memcache安装以及php_memcache.dll 扩展安装
php_memcache.dll扩展下载地址:http://windows.php.net/downloads/pecl/releases/memcache/3.0.8/ 下载注意事项:选择匹配自己环 ...
- emoji & click copy
emoji & click copy document.execCommand("copy"); https://clipboardjs.com/ https://www. ...
- Java之字符流操作-复制文件
package test_demo.fileoper; import java.io.*; /* * 字符输入输出流操作,复制文件 * 使用缓冲流扩展,逐行复制 * */ public class F ...
- spring boot 系列之六:深入理解spring boot的自动配置
我们知道,spring boot自动配置功能可以根据不同情况来决定spring配置应该用哪个,不应该用哪个,举个例子: Spring的JdbcTemplate是不是在Classpath里面?如果是,并 ...
- IDEA中新建Module时Module name、Content root、Module file location的含义
如下图测试: 最开始默认情况下,Content root.Module file location两行,最末尾的数据跟Module name是相同的. 现在对三行数据,强制进行不同的命名,Finish ...
- MT【187】余弦的线性组合
已知$\alpha+\beta+\gamma=\pi,(\alpha,\beta,\gamma\ge0)$ 求:$3\cos\alpha+4\cos\beta+5\cos\gamma$的最大值____ ...
