deeplearning.ai学习LSTM

一、LSTM架构与公式

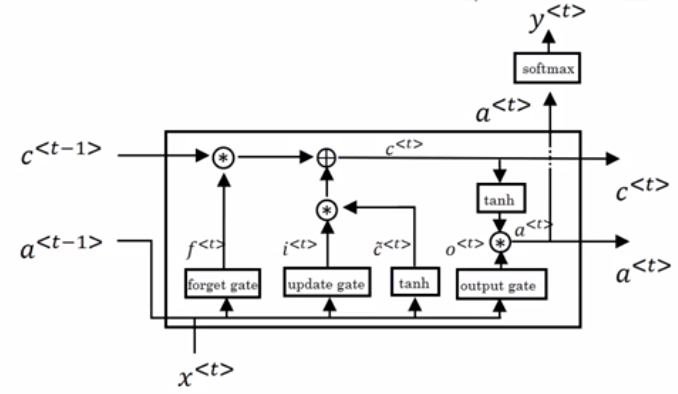
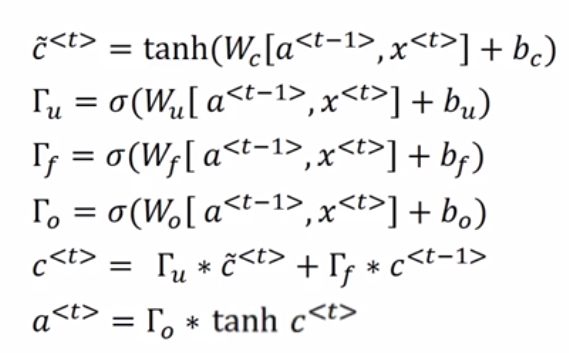
这里的a<t>表示的就是原始输出，y<t>表示的就是经过softmax的输出，c<t>相当于状态。u(update)代表是输入门，f代表遗忘门，o(output)代表输出门。

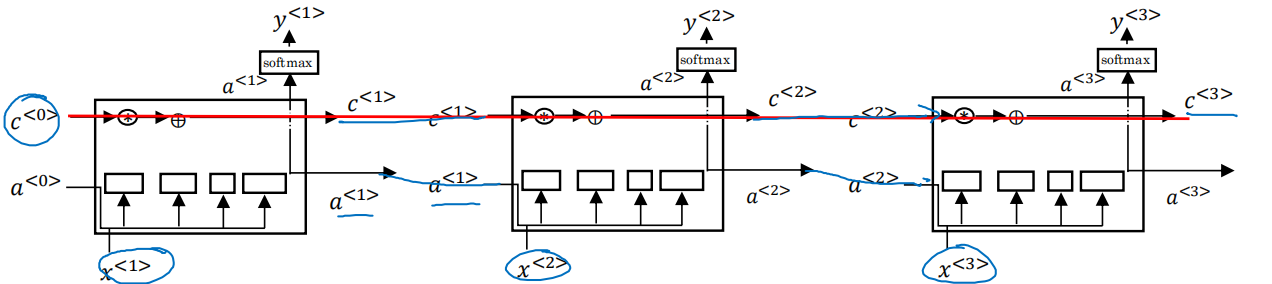
上图就是串联起来的结构，从图中我们可以看出，如果门控设置比较合理的话，c<0>从左到右是可以一直传递的，无论中间经过多少层，这就是LSTM可以处理长依赖的优势。

二、Bidirectional RNN(双向RNN结构)

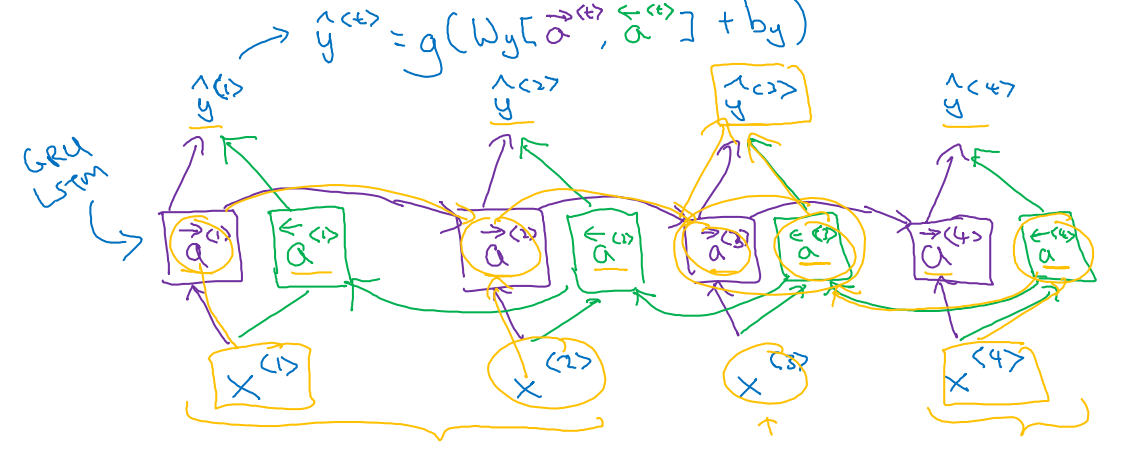
上图就是andrew ng画的双向RNN的结构示意图，该结构还是以序列标注的问题作为例子解释的。从图示可以看出，一个是从左到右计算a<1>--->a<2>--->a<3>--->a<4>，另一个方向是从右向左计算a<4>--->a<3>--->a<2>--->a<1>，根据最终两个方向计算出来的a<t>来计算最终的输出y<t>。计算公式如下：

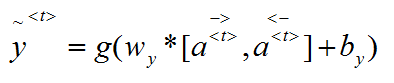
上图每一个节点cell可以是普通RNN结构，也可以是GRU或者LSTM。

三、Deep RNN

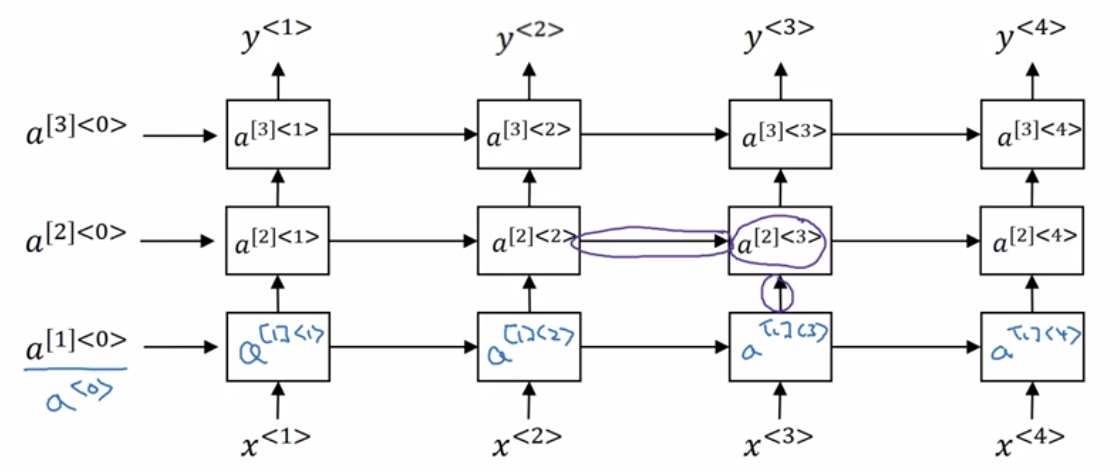
如图所示的深层RNN共有三层，RNN对于计算资源要求比较高，所以三层已经不少了，其各个节点a和输出值y计算如下：

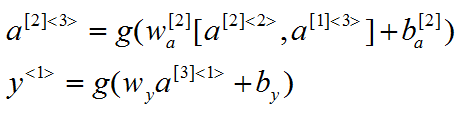
其中的每个方框节点cell，同样可以是普通RNN，GRU或者LSTM.