AC自动机学习笔记-2（Trie图&&last优化）

我是连月更都做不到的蒟蒻博主QwQ

考虑到我太菜了，考完noip就要退役了，所以我决定还是把博客的倒数第二篇博客给写了，也算是填了一个坑吧。（最后一篇？当然是悲怆のnoip退役记啦QAQ）

所以我们今天学习的是AC自动机的Trie图和last优化。如果不知道什么是AC自动机，建议看一看我的上一篇博客：AC自动机学习笔记1

Trie图

上次我们说到朴素的AC自动机的时间复杂度是布星的，原因如下：

匹配时因为每次都要跳fail边，复杂度上界可以达到 $ O(ml) $

而Tire图就是用来解决这种问题的。可以想到，匹配时跳fail边是十分浪费时间的。举个例子，对于字符集{a,b,c}上的模式ab,aab,aaab,aaaab,ac和文本串aaaac，它们建出来的AC自动机和匹配过程是这样的（蓝色边是Trie树的边，红色边是fail指针，黄色边是匹配时的状态转移）：

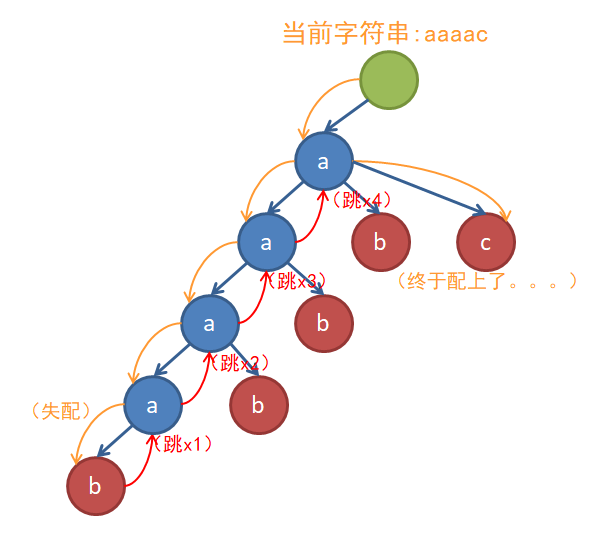
我们会想，如果失配时可以一步到位就好了。每次跳fail边的过程是固定的：一直跳，直到找到拥有儿子c的节点为止。也就是说，无论什么时候在这个节点上失配，只要你找的是字符c，你总会在固定的节点上重新开始匹配。既然这样，不如直接把那个字符为c的节点变成自己的儿子，就可以省去跳fail边的麻烦：

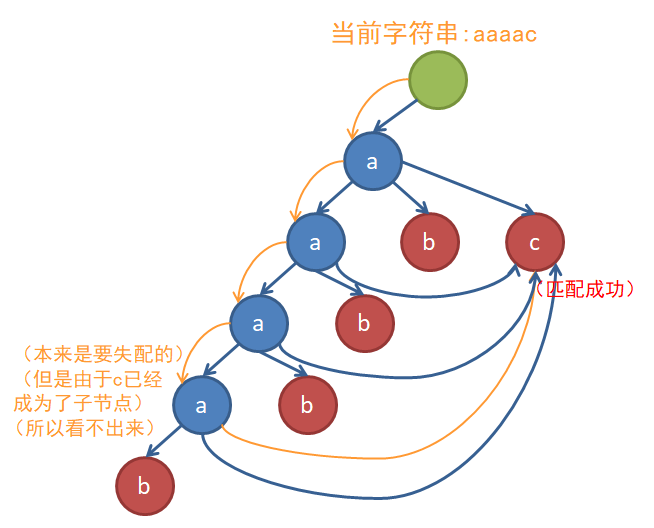
上图中，所有的节点的a,b,c三个子节点都是满的（未画出的边都指向根节点，表示完全失配只能从根重新开始）。这样，原本是DAG结构的AC自动机上出现了环，这样的结构我们称之为Trie图。于是乎，在匹配的时候我们终于可以不用考虑fail边，一口气不停地匹配到底辣٩(๑>◡<๑)۶复杂度变成了真正的 $ O(m) $ ，所以你就可以拿这个算法去爆踩std啦qwq

那么，怎么利用fail指针将AC自动机转化为Trie图呢？其实，只需要在构建fail指针时顺便修改子节点就行了：

void build()
{
    queue<int>q;
    q.push(1);
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(int i=0;i<26;++i)
        {
            int c=ch[x][i];
            if(!c){ch[x][i]=ch[fail[x]][i];continue;}//关键，把子节点改成fail节点的子节点
            q.push(c);
            int fa=fail[x];
            while(fa&&!ch[fa][i])fa=fail[fa];
            fail[c]=ch[fa][i];
        }
    }
}

因为当你遍历到这个节点时，fail节点的所有儿子肯定已经求出来了，所以直接用fail节点的子节点就好了。

last优化

上述方法将建图+匹配的复杂度成功优化为了 $ O(\sum n+m) $ ，但是别忘了，匹配成功时的计数也是需要跳fail边的。然而，为了跳到一个结束节点，我们可能需要中途跳到很多没用的伪结束节点：

如果一个节点的fail指向一个结尾节点，那么这个点也成为一个（伪）结尾节点。在匹配时，如果遇到结尾节点，就进行相应的计数处理。

这里面就又有优化的余地了：对于不是真正结束节点的伪结束点，直接跳过它就好了。我们用一个last指针表示“在它顶上的fail边所指向的一串节点中，第一个真正的结束节点”。于是，每次计数处理时，我们不跳fail边，改为跳last边，省去了很多冗余操作。

获得last指针的方法也十分简单，就是在void build()中加一句话：

last[c]=end[fail[c]]?fail[c]:last[fail[c]];

然后匹配时的代码就变成了：

void count(int x)
{
    while(x)
    {
       //计数、打印等，视题目要求顶
        x=last[x];
    }
}

void match()
{
    int now=1;
    for(int i=1;s[i]!='\0';++i)
    {
        int x=s[i]-'a';
        now=ch[now][x];
        if(end[now])count(now);
        else if(last[now])count(last[now]);
    }
}

注意：last优化是对复杂度没有影响的小优化，但是大多数情况下效果明显，类似于搜索剪枝。

总结

trie图和last优化都是在“如何跳过不必要的操作”上进行思考后的产物。这种思想可以被运用在很多题目里面，往往可以把复杂度里的一个n给去掉或者变成log。（不存在的。。。所谓“把某种方法完全掌握就可以轻松做出所有这种题”是某C姓教练最喜欢说的话，他认为“没做出一道要用到某种数据结构的题”的原因是“对某种数据结构的掌握还是不够熟练”，进而认为最好且明智的解决方法就是“多刷这种数据结构的题以提高熟练度”。这种人实在不好评价，我们还非得听他的话。。。）

AC自动机学习笔记就告一段落了，写这样一篇博客真的很费劲，感谢您的资瓷啦qwq！