treap（堆树）

# 2018-09-27 17:35:58 我实现的这个treap不能算是堆。有问题

　　最近对堆这种结构有点感兴趣，然后想用指针的方式实现一个堆而不是利用数组这种结构，于是自己想到了一个用二叉树结构实现堆的算法，下面是主要操作的源码：

　　头文件：

#ifndef _HEAP_H__
#define _HEAP_H__

#include <iostream>
#include <vector>

template<class type>
class BaseNode {
private:
	type val;
	BaseNode *left, *right;
public:
	BaseNode() {}
	BaseNode(type v) : val(v), left(nullptr), right(nullptr) {}
	/**/
	void value(type val) { this->val = val; }
	void lchild(BaseNode *left) { this->left = left; }
	void rchild(BaseNode *right) { this->right = right; }
	type value() { return val; }
	BaseNode* lchild() { return left; }
	BaseNode* rchild() { return right; }
};

template<class type>
class treap : protected BaseNode<type> {
	BaseNode<type> *root;
	size_t count;
public:
	treap() : root(nullptr), count(0) {}
	treap(std::vector<type> iter_type_vec) {
		for (int i = 0; i < iter_type_vec.size(); i++)
			insert(iter_type_vec[i]);
	}
	~treap() {
		delete root;
	}
	bool empty() const {
		if (count == 0)
			return true;
		return false;
	}
	size_t size() const {
		return count;
	}
	type top() const {
		if (empty())
		{
			std::cout << "Underflow!" << std::endl;
			return -1;
		}
		return root->value();
	}
	void show() const {
		travel(root);
		std::cout << std::endl;
	};
	void insert(type val);
	void remove();
	void travel(BaseNode<type> *pr) const;
};

#endif // _HEAP_H__

　　定义函数的实现：

#include "Heap.h"

template<class type>
void treap<type>::insert(type val)
{
	BaseNode<type> *node = new BaseNode<type>(val);
	if (!root)
		root = node;
	else if (root->value() <= val)
	{
		node->lchild(root);
		root = node;
	}
	else
	{
		if (root->lchild() && root->rchild()) {
			BaseNode<type> *pr = root;
			while (pr) {
				if (pr->lchild() && pr->lchild()->value() > val)
					pr = pr->lchild();
				else if (pr->rchild() && pr->rchild()->value() > val)
					pr = pr->rchild();
				else
					break;
			}
			if (!pr->lchild())
				pr->lchild(node);
			else if (!pr->rchild())
				pr->rchild(node);
			else {
				BaseNode<type> *tem = pr->lchild();
				pr->lchild(node);
				node->lchild(tem);
			}
		}
		else if (!root->lchild())
			root->lchild(node);
		else
			root->rchild(node);
	}
	++count;
}

template<class type>
void treap<type>::remove()
{
	if (!empty())
	{
		if (root->lchild() && root->rchild())
		{
			if (root->lchild()->value() > root->rchild()->value())
			{
				BaseNode<type> *rr = root->rchild();
				root = root->lchild();
				BaseNode<type> *tem = root->rchild();
				if (!tem)
					root->rchild(rr);
				else {
					BaseNode<type> *pr = root->rchild();
					while (pr) {
						if (pr->lchild() && pr->lchild()->value() > rr->value())
							pr = pr->lchild();
						else if (pr->rchild() && pr->rchild()->value() > rr->value())
							pr = pr->rchild();
						else
							break;
					}
					if (!pr->lchild())
						pr->lchild(rr);
					else
						pr->lchild(rr);
				}
			}
			else {
				BaseNode<type> *rr = root->lchild();
				root = root->rchild();
				BaseNode<type> *tem = root->lchild();
				if (!tem)
					root->lchild(rr);
				else {
					BaseNode<type> *pr = root->lchild();
					while (pr) {
						if (pr->lchild() && pr->lchild()->value() > rr->value())
							pr = pr->lchild();
						else if (pr->rchild() && pr->rchild()->value() > rr->value())
							pr = pr->rchild();
						else
							break;
					}
					if (!pr->lchild())
						pr->lchild(rr);
					else
						pr->rchild(rr);
				}
			}
		}
		else if (root->lchild())
			root = root->lchild();
		else
			root = root->rchild();
		--count;
	}
}

template<class type>
void treap<type>::travel(BaseNode<type> *pr) const
{
	if (pr) {
		std::cout << pr->value() << ' ';
		travel(pr->lchild());
		travel(pr->rchild());
	}
}

　　测试：

#include <iostream>
#include <vector>
#include "Heap.cpp"

int main()
{
    std::vector<int> nums{1,5,3,2,4};
    treap<int> trees;

    for (auto v : nums)
        trees.insert(v);

    std::cout << "当前堆节点个数：" << trees.size() << std::endl;

    std::cout << "遍历堆树：";
    trees.show();
    std::cout << std::endl;

    while (!trees.empty()) {
        std::cout << "当前堆顶数据：" << trees.top() << std::endl;
        trees.remove();
    }

    return 0;
}

　　运行结果：

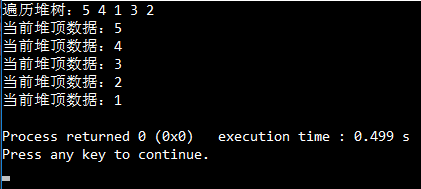
　　在Windows上VS和CodeBlocks上都测试成功了，VS上是代码都在一个文件中测试的，codeblocks上不知道为什么必须用 #include "Heap.cpp" 而不能用 #include "Heap.h"，否则会报错。。。

　　CentOS7 gcc 8.1.0也测试成功了：