SPFA（）判环

1 SPFA（）判负环

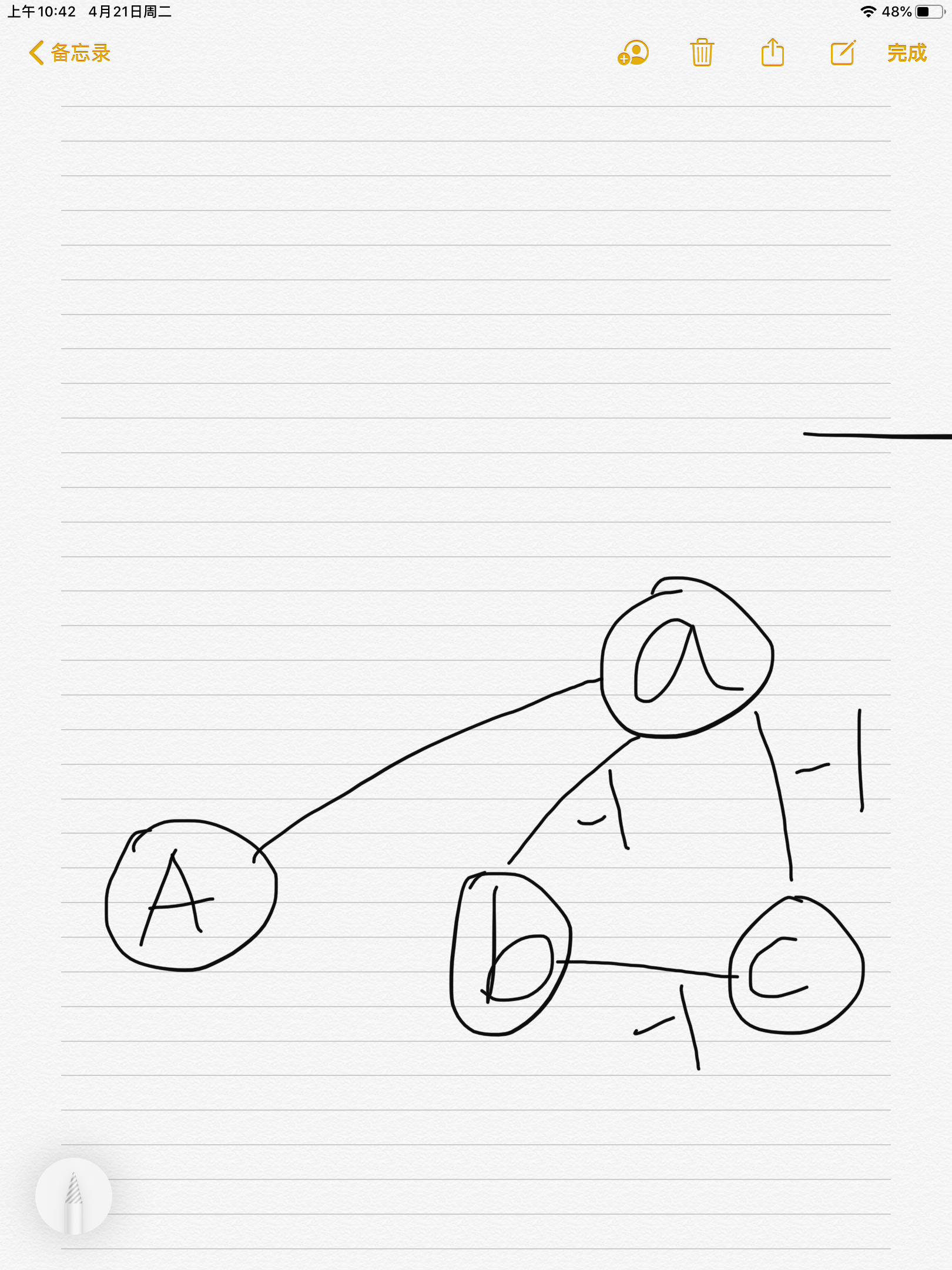
SPFA（）判负环的原理就是在求最短路的过程中，如果存在负环，比如说要求从A到a的最短距离，设为s,但是经过a->c->b->a可以更短，所以如果一直经过a->c->b的话，会一直减小。所以说程序会一直对a进行是松弛，那么最多松弛多少次我们会发现有环呢?,答案是n次（n为点的个数）。(至于为什么，还不太理解以后再补吧)

code:

void add(int x,int y,int z){
    edge[cnt].to=y;
    edge[cnt].weight=z;
    edge[cnt].nxt=head[x];
    head[x]=cnt++;
}
bool SPFA(){
    queue<int >que;
    que.push();
    mark[]=;
    dis[]=;
    num[]=;
    while(que.size()){
        int u=que.front();
        que.pop();
        mark[u]=;
        for(int i=head[u];i!=-;i=edge[i].nxt){
            int v=edge[i].to;
            if(dis[v]>dis[u]+edge[i].weight){
                dis[v]=dis[u]+edge[i].weight;
                if(!mark[v]) {
                    mark[v]=;
                    num[v]++;
                    if(num[v]>=n) return ;
                    que.push(v);
                }
            }
        }
    }
    return ;
}

2 SPFA()判正环

判断正环是在最长路的基础上判断的， 原理个判负环一样，当存在正环时，正环会让环外一点到环上一点的距离无限增大。代码就是将判断条件换成 dis[v]<dis[u]+edge[i].weight.