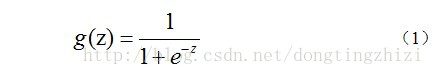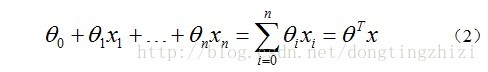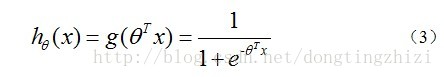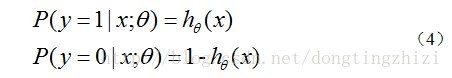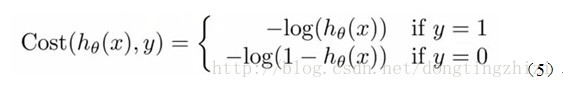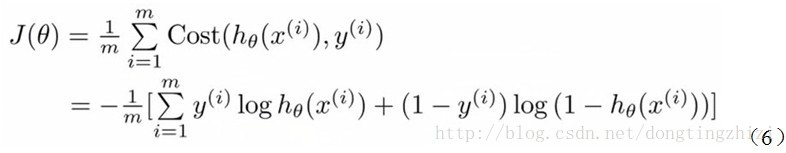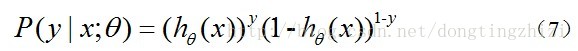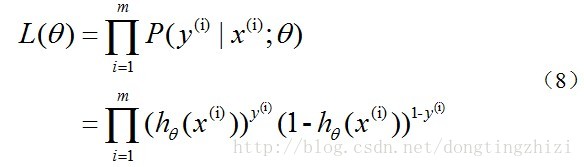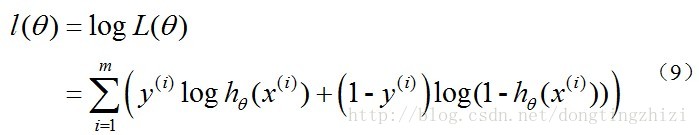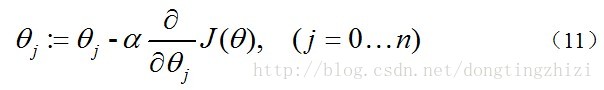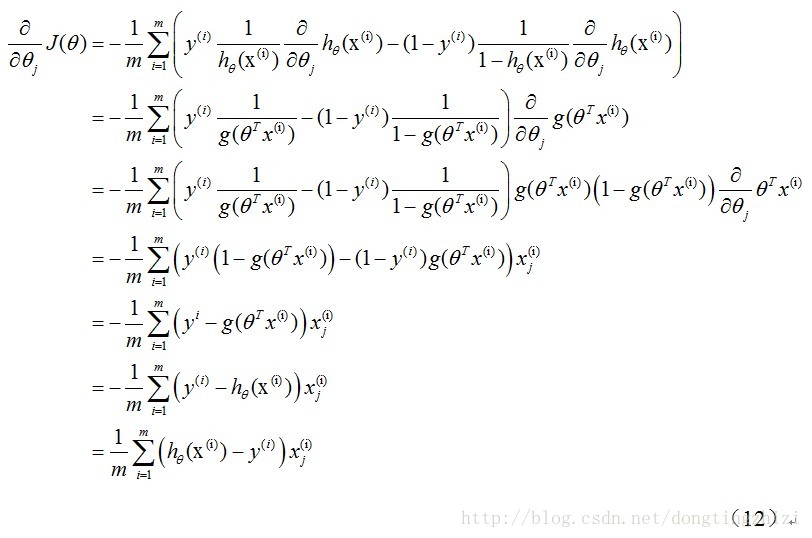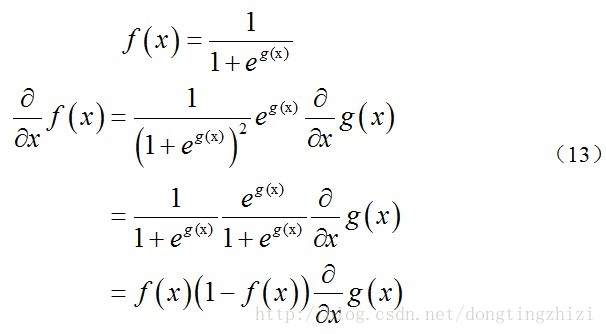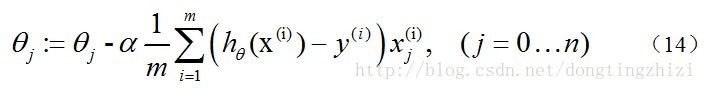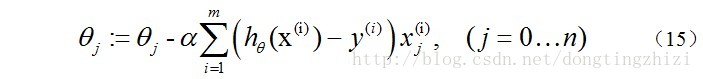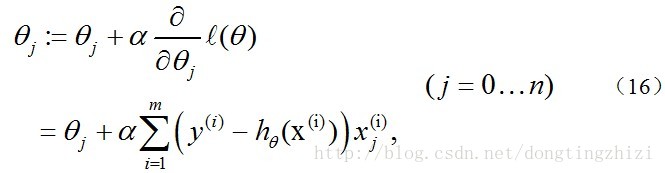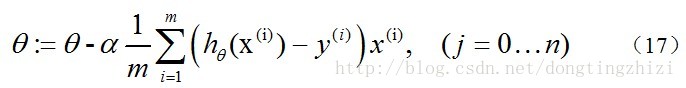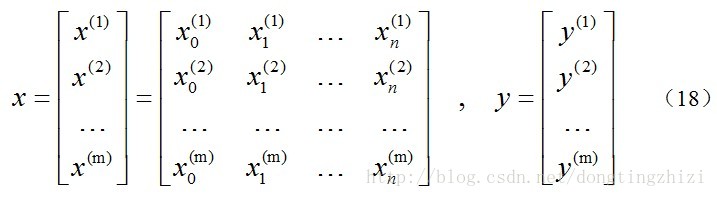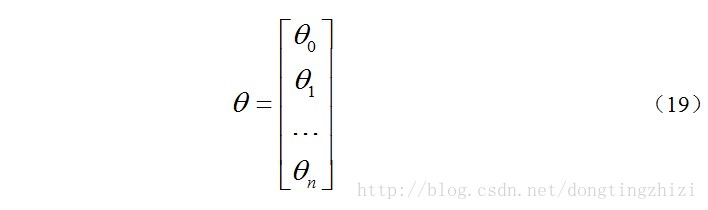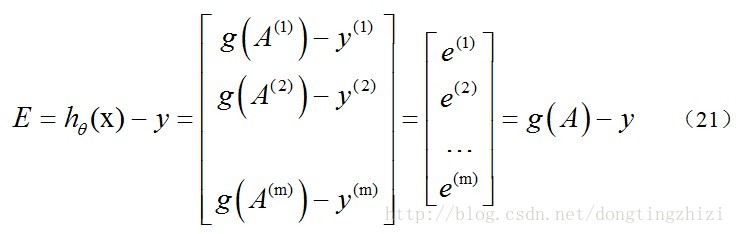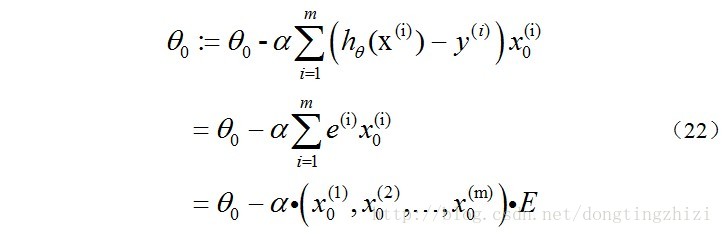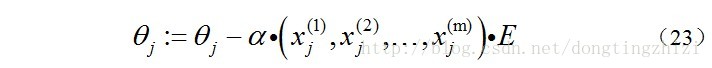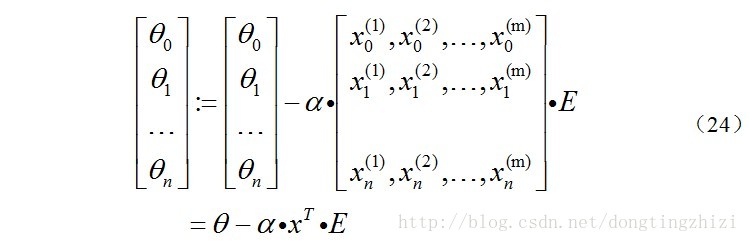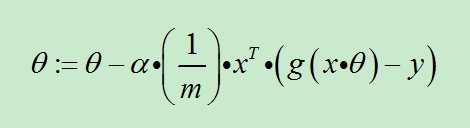转载-Logistic回归总结
Logistic回归总结
作者:洞庭之子
微博:洞庭之子-Bing
(2013年11月)
1.引言
看了Stanford的Andrew Ng老师的机器学习公开课中关于Logistic Regression的讲解,然后又看了《机器学习实战》中的LogisticRegression部分,写下此篇学习笔记总结一下。
首先说一下我的感受,《机器学习实战》一书在介绍原理的同时将全部的算法用源代码实现,非常具有操作性,可以加深对算法的理解,但是美中不足的是在原理上介绍的比较粗略,很多细节没有具体介绍。所以,对于没有基础的朋友(包括我)某些地方可能看的一头雾水,需要查阅相关资料进行了解。所以说,该书还是比较适合有基础的朋友。
本文主要介绍以下三个方面的内容:
(1)Logistic Regression的基本原理,分布在第二章中;
(2)Logistic Regression的具体过程,包括:选取预测函数,求解Cost函数和J(θ),梯度下降法求J(θ)的最小值,以及递归下降过程的向量化(vectorization),分布在第三章中;
(3)对《机器学习实战》中给出的实现代码进行了分析,对阅读该书LogisticRegression部分遇到的疑惑进行了解释。没有基础的朋友在阅读该书的Logistic Regression部分时可能会觉得一头雾水,书中给出的代码很简单,但是怎么也跟书中介绍的理论联系不起来。也会有很多的疑问,比如:一般都是用梯度下降法求损失函数的最小值,为何这里用梯度上升法呢?书中说用梯度上升发,为何代码实现时没见到求梯度的代码呢?这些问题在第三章和第四章中都会得到解答。
文中参考或引用内容的出处列在最后的“参考文献”中。文中所阐述的内容仅仅是我个人的理解,如有错误或疏漏,欢迎大家批评指正。下面进入正题。
2. 基本原理
Logistic Regression和Linear Regression的原理是相似的,按照我自己的理解,可以简单的描述为这样的过程:
(1)找一个合适的预测函数(Andrew Ng的公开课中称为hypothesis),一般表示为h函数,该函数就是我们需要找的分类函数,它用来预测输入数据的判断结果。这个过程时非常关键的,需要对数据有一定的了解或分析,知道或者猜测预测函数的“大概”形式,比如是线性函数还是非线性函数。
(2)构造一个Cost函数(损失函数),该函数表示预测的输出(h)与训练数据类别(y)之间的偏差,可以是二者之间的差(h-y)或者是其他的形式。综合考虑所有训练数据的“损失”,将Cost求和或者求平均,记为J(θ)函数,表示所有训练数据预测值与实际类别的偏差。
(3)显然,J(θ)函数的值越小表示预测函数越准确(即h函数越准确),所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法,Logistic
Regression实现时有的是梯度下降法(Gradient Descent)。
3. 具体过程
3.1 构造预测函数
Logistic Regression虽然名字里带“回归”,但是它实际上是一种分类方法,用于两分类问题(即输出只有两种)。根据第二章中的步骤,需要先找到一个预测函数(h),显然,该函数的输出必须是两个值(分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
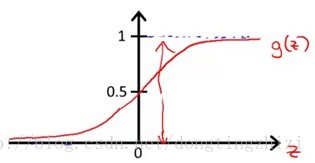
对应的函数图像是一个取值在0和1之间的S型曲线(图1)。
图1
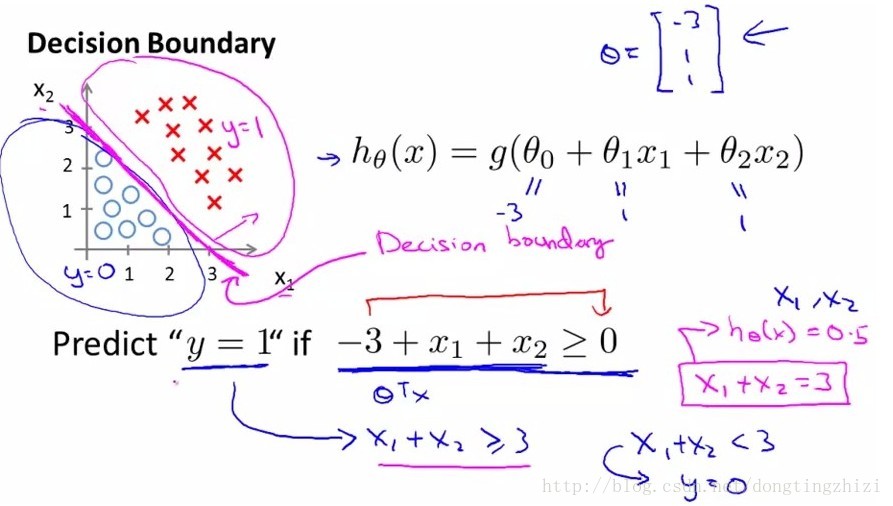
接下来需要确定数据划分的边界类型,对于图2和图3中的两种数据分布,显然图2需要一个线性的边界,而图3需要一个非线性的边界。接下来我们只讨论线性边界的情况。
图2
图3
对于线性边界的情况,边界形式如下:
构造预测函数为:
hθ(x)函数的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
3.2 构造Cost函数
Andrew Ng在课程中直接给出了Cost函数及J(θ)函数如式(5)和(6),但是并没有给出具体的解释,只是说明了这个函数来衡量h函数预测的好坏是合理的。
实际上这里的Cost函数和J(θ)函数是基于最大似然估计推导得到的。下面详细说明推导的过程。(4)式综合起来可以写成:
取似然函数为:
对数似然函数为:
最大似然估计就是要求得使l(θ)取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew
Ng的课程中将J(θ)取为(6)式,即:
因为乘了一个负的系数-1/m,所以J(θ)取最小值时的θ为要求的最佳参数。
3.3 梯度下降法求J(θ)的最小值
求J(θ)的最小值可以使用梯度下降法,根据梯度下降法可得θ的更新过程:
式中为α学习步长,下面来求偏导:
上式求解过程中用到如下的公式:
因此,(11)式的更新过程可以写成:
因为式中α本来为一常量,所以1/m一般将省略,所以最终的θ更新过程为:
另外,补充一下,3.2节中提到求得l(θ)取最大值时的θ也是一样的,用梯度上升法求(9)式的最大值,可得:
观察上式发现跟(14)是一样的,所以,采用梯度上升发和梯度下降法是完全一样的,这也是《机器学习实战》中采用梯度上升法的原因。
3.4 梯度下降过程向量化
关于θ更新过程的vectorization,Andrew Ng的课程中只是一带而过,没有具体的讲解。
《机器学习实战》连Cost函数及求梯度等都没有说明,所以更不可能说明vectorization了。但是,其中给出的实现代码确是实现了vectorization的,图4所示代码的32行中weights(也就是θ)的更新只用了一行代码,直接通过矩阵或者向量计算更新,没有用for循环,说明确实实现了vectorization,具体代码下一章分析。
文献[3]中也提到了vectorization,但是也是比较粗略,很简单的给出vectorization的结果为:
且不论该更新公式正确与否,这里的Σ(...)是一个求和的过程,显然需要一个for语句循环m次,所以根本没有完全的实现vectorization,不像《机器学习实战》的代码中一条语句就可以完成θ的更新。
下面说明一下我理解《机器学习实战》中代码实现的vectorization过程。
约定训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同的特称取值:
约定待求的参数θ的矩阵形式为:
先求x.θ并记为A:
求hθ(x)-y并记为E:
g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。由上式可知hθ(x)-y可以由g(A)-y一次计算求得。
再来看一下(15)式的θ更新过程,当j=0时:
同样的可以写出θj,
综合起来就是:
综上所述,vectorization后θ更新的步骤如下:
(1)求A=x.θ;
(2)求E=g(A)-y;
(3)求θ:=θ-α.x'.E,x'表示矩阵x的转置。
也可以综合起来写成:
前面已经提到过:1/m是可以省略的。
4. 代码分析
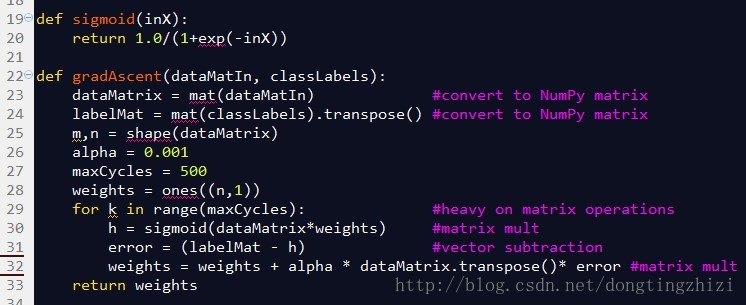
图4中是《机器学习实战》中给出的部分实现代码。
图4
sigmoid函数就是前文中的g(z)函数,参数inX可以是向量,因为程序中使用了Python的numpy。
gradAscent函数是梯度上升的实现函数,参数dataMatin和classLabels为训练数据,23和24行对训练数据做了处理,转换成numpy的矩阵类型,同时将横向量的classlabels转换成列向量labelMat,此时的dataMatrix和labelMat就是(18)式中的x和y。alpha为学习步长,maxCycles为迭代次数。weights为n维(等于x的列数)列向量,就是(19)式中的θ。
29行的for循环将更新θ的过程迭代maxCycles次,每循环一次更新一次。对比3.4节最后总结的向量化的θ更新步骤,30行相当于求了A=x.θ和g(A),31行相当于求了E=g(A)-y,32行相当于求θ:=θ-α.x'.E。所以这三行代码实际上与向量化的θ更新步骤是完全一致的。
总结一下,从上面代码分析可以看出,虽然只有十多行的代码,但是里面却隐含了太多的细节,如果没有相关基础确实是非常难以理解的。相信完整的阅读了本文,就应该没有问题了!^_^。
【参考文献】
[1]《机器学习实战》——【美】Peter Harington
[2] Stanford机器学习公开课(https://www.coursera.org/course/ml)
[3] http://blog.csdn.net/abcjennifer/article/details/7716281
[4] http://www.cnblogs.com/tornadomeet/p/3395593.html
[5] http://blog.csdn.net/moodytong/article/details/9731283
[6] http://blog.csdn.net/jackie_zhu/article/details/8895270
转载-Logistic回归总结的更多相关文章
- 转载:Logistic回归原理及公式推导
转载自:AriesSurfer 原文见 http://blog.csdn.NET/acdreamers/article/details/27365941 Logistic回归为概率型非线性回归模型,是 ...
- 转载 Deep learning:六(regularized logistic回归练习)
前言: 在上一讲Deep learning:五(regularized线性回归练习)中已经介绍了regularization项在线性回归问题中的应用,这节主要是练习regularization项在lo ...
- 【转载】logistic回归
原文地址:https://www.cnblogs.com/zichun-zeng/p/3824745.html 1. logistic回归与一般线性回归模型的区别: (1) 线性回归的结果变量 ...
- 如何在R语言中使用Logistic回归模型
在日常学习或工作中经常会使用线性回归模型对某一事物进行预测,例如预测房价.身高.GDP.学生成绩等,发现这些被预测的变量都属于连续型变量.然而有些情况下,被预测变量可能是二元变量,即成功或失败.流失或 ...
- 机器学习笔记—Logistic回归
本文申明:本系列笔记全部为原创内容,如有转载请申明原地址出处.谢谢 序言:what is logistic regression? Logistics 一词表示adj.逻辑的;[军]后勤学的n.[逻] ...
- 机器学习简易入门(四)- logistic回归
摘要:使用logistic回归来预测某个人的入学申请是否会被接受 声明:(本文的内容非原创,但经过本人翻译和总结而来,转载请注明出处) 本文内容来源:https://www.dataquest.io/ ...
- 第三集 欠拟合与过拟合的概念、局部加权回归、logistic回归、感知器算法
课程大纲 欠拟合的概念(非正式):数据中某些非常明显的模式没有成功的被拟合出来.如图所示,更适合这组数据的应该是而不是一条直线. 过拟合的概念(非正式):算法拟合出的结果仅仅反映了所给的特定数据的特质 ...
- 对线性回归,logistic回归和一般回归的认识
原文:http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html#3281650 对线性回归,logistic回归和一般回归的认识 ...
- 机器学习实战笔记5(logistic回归)
1:简单概念描写叙述 如果如今有一些数据点,我们用一条直线对这些点进行拟合(改线称为最佳拟合直线),这个拟合过程就称为回归.训练分类器就是为了寻找最佳拟合參数,使用的是最优化算法. 基于sigmoid ...
随机推荐
- FFmpeg笔记-基本使用
FFmpeg是目前最牛逼的开源跨平台音视频处理工具. 准备知识 我不是音视频编解码出身的,对于这一块非常的不了解,导致在学习FFmpeg的时候云里雾里的,所以学习之前最好看些资料对音视频编解码有点认识 ...
- Golang 如何交叉编译
Golang 支持交叉编译,即在一个平台上生成另一个平台的可执行程序.方法如下: Mac 下编译 Linux 和 Windows 64位可执行程序 CGO_ENABLED=0 GOOS=linux G ...
- BZOJ 4166: 月宫的符卡序列
如果使用回文树,节点 \(u\) 的回文串和 \(fail_u\) 的回文串中心不一样,因为回文树的 \(fail\) 指针指向的是最长回文后缀,没法快速解决异或和 考虑魔改回文树,用马拉车来解决,扩 ...
- Python字符串(一)
一.get char 1.获取单个字符 字符串中的每一个字符都会对应一个唯一的下标(索引)用来表示字符串中的位置.下标从0开始依次增加:0对应的是第一个字符:也可以从从-1开始依次减小,-1代表最后一 ...
- HDU 5506:GT and set bitset+暴力
GT and set Accepts: 35 Submissions: 194 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 655 ...
- 第1节 storm编程:4、storm环境安装以及storm编程模型介绍
dataSource:数据源,生产数据的东西 spout:接收数据源过来的数据,然后将数据往下游发送 bolt:数据的处理逻辑单元.可以有很多个,基本上每个bolt都处理一部分工作,然后将数据继续往下 ...
- c++中比较好用的“黑科技”
切入正题,上黑科技 一.黑科技函数(常用的我就不写了,例如sort函数) 1.next_permutation(a+1,a+1+n) a[1-n]全排列 2.reverse(a+1,a+1+n) 将a ...
- 针对小文件的spark wholeTextFiles()
场景:推送过来的数据文件数量很多,并且每个只有10-30M的大小 spark读取hdfs一般都是用textfile(),但是对于这种情况,如果使用textFile默认产生的分区数将与文件数目一致,产生 ...
- redis长篇介绍
一. 简介 Redis 完全开源免费,遵守BSD协议,高性能的(NOSQL) key-value数据库 BSD 伯克利软件发行版 缓存数据集 所以都在内存上面 Redis 数据类型分为:字符串类型.散 ...
- CSS-text-intent
text-indent:[ <length> | <percentage> ] && ? && ? 默认值:0 适用于:块容器 继承性:有 动画 ...