python --内建结构 汉诺塔结构

规则：

　　1.每次移动一个盘子

　　2.任何时候大盘子在下面，小盘子在上面

方法：

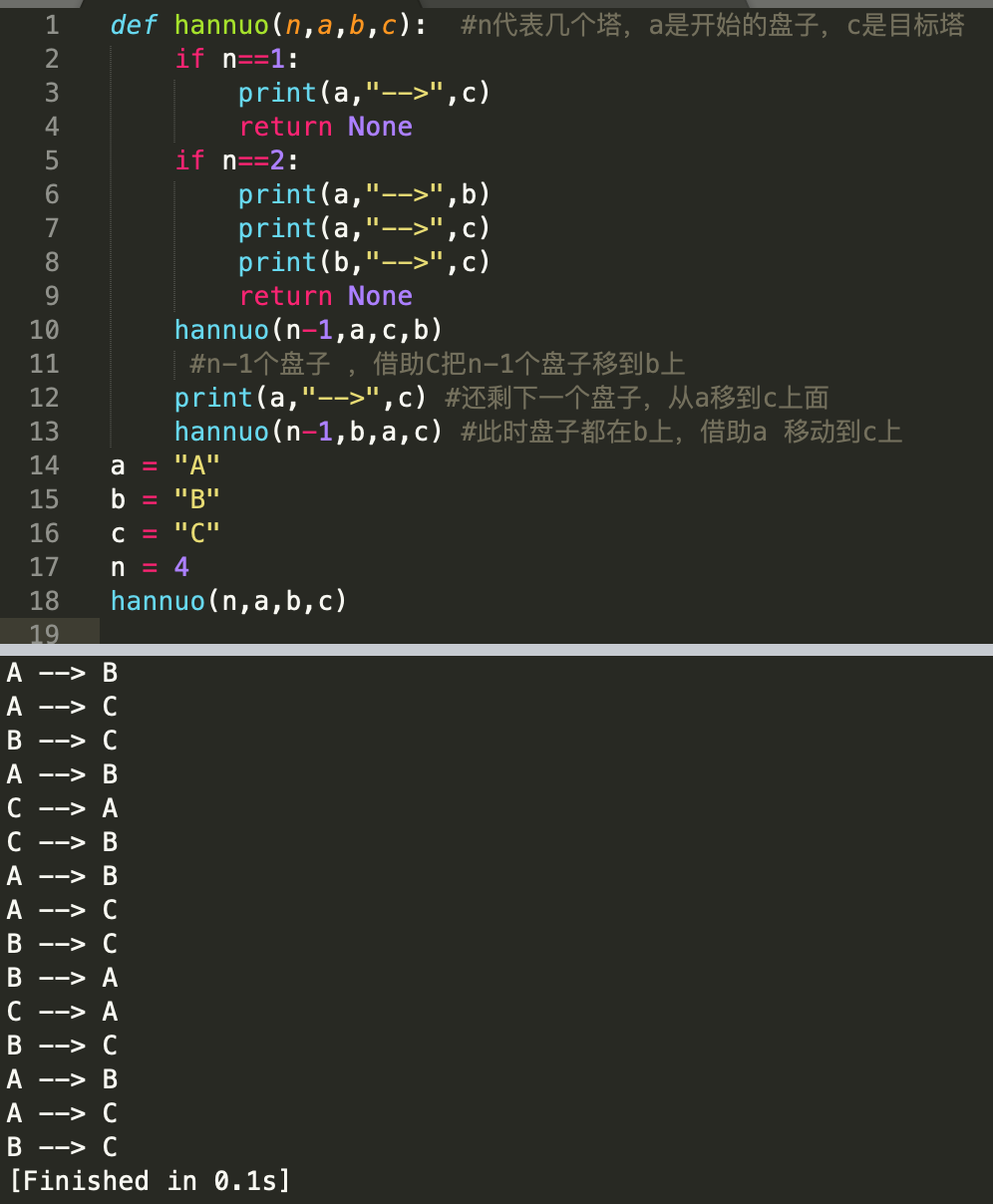
　　1.n=1:直接将A上的盘子移动到c 上面，A->C

　　2.n=2:

　　　　1>A->B

　　　　2>A->C

　　　　3>B->C

　　3.n=3:

　　　　1.把A上面两个盘子，通过C移动到B上面，通过递归实现

　　　　2.把A上面剩下的一个最大的盘子移动到C上面，A—>C

　　　　3.把B上面的盘子借助A，移到C上，调用递归

　　　4.n=n:

　　　　1.把A上的N-1个盘子借助C，移动到B上，通过递归实现；

　　　　2.把A上最大的盘子移动到C上，A->C

　　　　3.把B上n-1个盘子，借助A 移动到C上，调用递归