PageRank 算法初步了解

前言

因为想做一下文本自动摘要，文本自动摘要是NLP的重要应用，搜了一下，有一种TextRank的算法，可以做文本自动摘要。其算法思想来源于Google的PageRank，所以先把PageRank给了解一下。

马尔科夫链

我感觉说到PageRank，应该要提起马尔科夫链，因为PageRank在计算的过程中，和马尔科夫链转移是十分相似的，只是PageRank在马尔科夫链的转移上做了一些改动。

马尔科夫链的维基百科里是这么说的：

马尔可夫链是满足马尔可夫性质的随机变量序列\(X_{1}, X_{2}, X_{3}, ...\)。即给出当前状态，将来状态和过去状态是相互独立的。从形式上看，如果两边的条件分布有定义（即如果\(\Pr(X_{1}=x_{1},...,X_{n}=x_{n})>0\)则\(\Pr(X_{{n+1}}=x\mid X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{n}=x_{n})=\Pr(X_{{n+1}}=x\mid X_{n}=x_{n})\)。

\(Xi\)的可能值构成的可数集S叫做该链的“状态空间”。

形式定义好像有点复杂。我这里只想介绍自己所认识的马氏链，一个简单通俗易懂的马氏链。

假设有一个离散型随机变量\(w\)，表示的是当前社会中贫穷，中等和富有的人的概率，其初始分布是：\(w=(0.21,0.68,0.11)\) 表示社会中贫穷的人占28%，中等的人占68%，富有的人占11%，

这是初始状态，可以想象成这是我们所处地球的第一代人\(X_{1}\)（那个时候就有贫富差距了），接下来第一代人要生小孩，形成第二代人\(X_{2}\)，这个叫做状态的转移，从\(X_{1}\)转移到\(X_{2}\)。怎么转移呢，这是有一个概率的：

父代\子代	儿子是穷人	儿子是中等	儿子是富人
父亲是穷人	0.65	0.28	0.07
父亲是中等	0.15	0.67	0.18
父亲是富人	0.12	0.36	0.52

上述表格代表的是，父亲属于哪个阶级，那儿子属于某个阶级的概率。比如父亲是富人，儿子也是富人的概率是 0.52，这表示大概一半的富二代以后都会败光家产。所以根据以上表格，第二代\(X_{2}\)穷人的概率是 \(0.21*0.65+0.68*0.15+0.11*0.12=0.252\) 以上的计算过程实际上矩阵相乘，表格里的数据组成一个矩阵\(P\) 叫做概率转移矩阵

\[ P=\begin{bmatrix}
0.65 & 0.28 &0.07 \\
0.15 & 0.67 & 0.18 \\
0.12 & 0.36 & 0.52
\end{bmatrix}
\]

\[ X_{1} \cdot P = X_{2} = \begin{Bmatrix}
0.252 & 0.554 &0.194
\end{Bmatrix}
\]

以此类推，不断计算，不断状态转移，我们发现从第7代开始，就稳定不变了：

\[ X_{3} = \begin{Bmatrix}
0.270 & 0.512 & 0.218
\end{Bmatrix} \\
X_{4} = \begin{Bmatrix}
0.278 & 0.497 & 0.225
\end{Bmatrix} \\
X_{5} = \begin{Bmatrix}
0.282 & 0.490 & 0.226
\end{Bmatrix} \\
X_{6} = \begin{Bmatrix}
0.285 & 0.489 & 0.225
\end{Bmatrix} \\
X_{7} = \begin{Bmatrix}
0.286 & 0.489 & 0.225
\end{Bmatrix} \\
X_{8} = \begin{Bmatrix}
0.286 & 0.489 & 0.225
\end{Bmatrix} \\
X_{9} = \begin{Bmatrix}
0.286 & 0.489 & 0.225
\end{Bmatrix} \\
\]

这不是偶然，从任意一个\(X_{1}\)的分布出发，经过概率转移矩阵，都会收敛到一个稳定的分布 \(\pi=\lbrace 0.286,0.489,0.225 \rbrace\)，从\(X_{1} \rightarrow X_{2} \rightarrow X_{3}....\rightarrow X_{n}\) 这个转移的链条就是马尔科夫链，它最终会收敛到稳定分布 \(\pi\)，也就是 \(\pi \cdot P = \pi\)，至于为什么会这样，肯定是和状态转移矩阵有关，最终的稳定分布不是由初始状态\(X_{1}\)决定的，而是由转移矩阵\(P\)决定的，具体就不细究了。

总之，我们得出这样一个结论，如果有一个随机变量分布为\(X\) 和状态转移矩阵\(P\)，随机变量分布的下一个状态\(X_{next}\) 可以由上一个状态\(X_{pre}\) 乘以矩阵\(P\)得来，那么经过n步迭代，最终会得到一个不变的，平稳的分布。

PageRank

PageRank 是谷歌搜索引擎的进行网页排名算法，它是把所有网页都构成一张图，每个网页是一个节点，如果一个网页中有链向其他网页的链接，那么就有一条有向边连接这两个点。

有了这张图可以干嘛吗？PageRank 认为，每条边都是一个投票动作，\(A \rightarrow B\) 是A在给B投票，B的权重就会增加。

举个例子就非常清楚了，假设互联网上一共就4个页面，全球几十亿网名，每天只能看这个4个web页面，这四个页面分别是A,B,C,D，其中B页面有两个超链接指向A,C，C中有1个超链接指向A，D中有三个超链接指向A。其画成一张图，就是这样的：

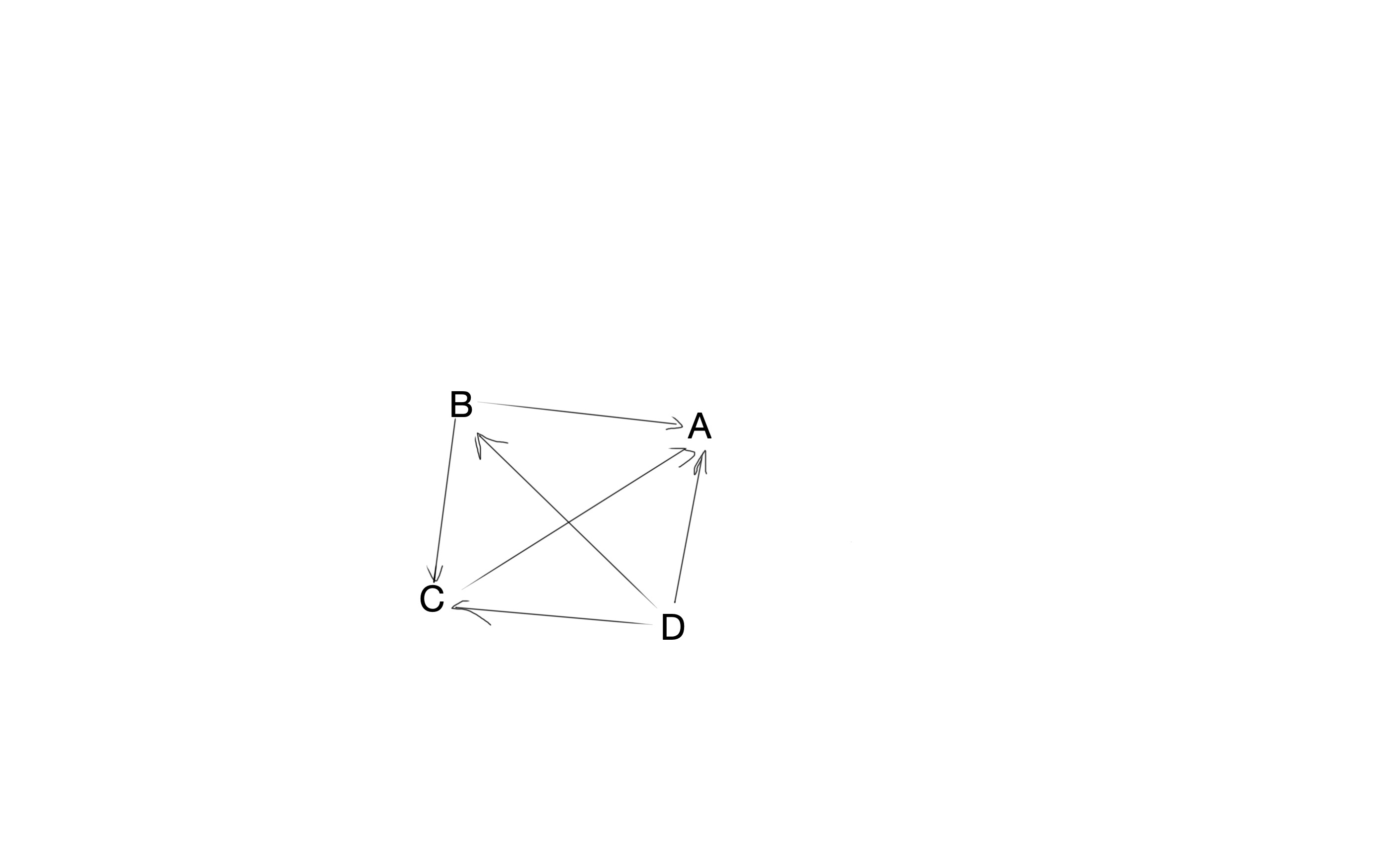
这里要清楚 PageRank 计算的值是什么，PageRank 计算的最终值，是每个网页被往点击浏览的概率，也就相当于权重。所以这还是一个离散型随机变量，\(W=\lbrace p_{a},p_{b},p_{c},p_{d} \rbrace , p_{a}+p_{b}+p_{c}+p_{d} = 1\)。一开始假设每个网页被浏览的概率都是相同的，每个页面被网民点击的概率都是0.25，\(W=\lbrace 0.25,0.25,0.25,0.25 \rbrace\)

PageRank 的计算过程就和上面所说的马尔科夫链一样，初始状态\(W_{0}\)就是全球网民同时上网，每个网民每次都只点击一次网页，每个网页被访问的概率。那么状态2 \(W_{1}\) 就是全体网民开始点击浏览第二个网页时，每个网页被访问的概率。PageRank 也有一个概率转移矩阵\(P\)，而\(P\)就存在于上图中，其中\(P_{i,j}\) 表i网页链向j的链接数除以i网页的所有外链数。 其实意思就是，当你访问到i网页的时候，有多大的概率访问j网页。所以对于某个特定的状态\(W_{n}\)，全体网民开始访问第n个网页，它是由上一个状态\(W_{n-1}\) 全体网民访问到第n-1个网页，通过某种概率得来。这和上面的穷人，富人非常相似。我们计算A页面在第n次，也就是状态n的时候被访问的概率

\[p_{a}^{n} = p_{b}^{n-1} * P_{b,a} + p_{c}^{n-1} * P_{c,a} + p_{d}^{n-1} * P_{d,a}
\]

所以

\[W_{1} = W_{0} \cdot P，P=\begin{Bmatrix}
0.000 & 0.000 & 0.000 & 0.000 \\
0.500 & 0.000 & 0.500 & 0.000 \\
1.000 & 0.000 & 0.000 & 0.000 \\
0.333 & 0.333 & 0.333 & 0.000
\end{Bmatrix}
\]

整个PageRank 计算直到得到平稳分布\(\pi\)，这就是最终每个网页被网民点击的概率，或者叫做权重，排名。

接下来咱们具体计算一下，上述四个页面A,B,C,D的最终权重是多少。我们写一段C++ 程序来模拟PageRank 的计算过程。

int main()
{
    int n=4;
    double d=0.85;
    double a[4]={0.25,0.25,0.25,0.25};

    double b[4][4]={{0,0,0,0},{1,0,1,0},{1,0,0,0},{1,1,1,0}};
    double linkNums[4]={0,2,1,3};

    printf("转移矩阵:\n");
    double p[4][4];
    for(int i=0;i<4;i++)
    {
        for(int j=0;j<4;j++)
        {
            p[i][j] = b[i][j]==0?0:b[i][j]/linkNums[i];
            printf("%.3f ",p[i][j]);
        }
        printf("\n");
    }
    printf("\n");
    printf("初始状态:\n");
    for(int i=0;i<4;i++)
    {
        printf("%.3f ",a[i]);
    }
    printf("\n");
    double c[4];
    int i=0;
    int pos=0;
    while(1)
    {

        for(int i=0;i<4;i++) {

            double x=0;

            for (int j = 0; j < 4; j++) {

                x+=a[j]*b[j][i];
            }
            c[i]=x;
            //c[i]=1.0*(1-d)/n + d*x;
        }

        int tag=0;
        for(int i=0;i<4;i++) {

            if(a[i] != c[i])
            {
                tag=1;
                a[i]=c[i];
            }
        }

        pos++;
        printf("状态%d :\n",pos);

        for(int i=0;i<4;i++)
        {
            printf("%.3f ",a[i]);
        }
        printf("\n");
        printf("\n");

        if(tag==0)
            break;

    }

}

其中p是转移矩阵，a是我们要求的随机变量的分布。

运行结果如下

转移矩阵:
0.000 0.000 0.000 0.000
0.500 0.000 0.500 0.000
1.000 0.000 0.000 0.000
0.333 0.333 0.333 0.000 

初始状态:
0.250 0.250 0.250 0.250
状态1 :
0.750 0.250 0.500 0.000 

状态2 :
0.750 0.000 0.250 0.000 

状态3 :
0.250 0.000 0.000 0.000 

状态4 :
0.000 0.000 0.000 0.000 

状态5 :
0.000 0.000 0.000 0.000

我们发现，到最后的平稳分布居然是\(\lbrace 0,0,0,0 \rbrace\)，为什么会发生这样的情况呢？因为D这个网页，没有任何网页链接到它，所以在转移的过程中，它的下一个状态肯定为0，又因为D变成0了，所以影响到它所链接的网页，最终会导致所有网页的概率值都变成0。

为了避免这样的情况，PageRank 引入了一个阻尼系数d和随机访问的概念 ,d是一个概率值在0-1之间，这个d的物理意义是当你浏览到一个网页的时候，继续点击网页中的链接浏览下一个网页的概率。那么1-d 表示的就是浏览到一个网页的时候，不通过网页中的链接，而是额外新开了一个窗口随机访问其他网页的概率。所以PageRank 认为访问网页，要么是通过网页中的链接点击，要么是随机访问。

有了这个阻尼系数d，原先图中的情况就发生变化了，每个网页，都有很多条隐形的边，指向所有其他的网页，这些隐形的边表示的是随机访问不通过链接点击。因此在计算A页面在第n次，也就是状态n的时候被访问的概率公式就要发生变化了

\[p_{a}^{n} = (p_{b}^{n-1} * P_{b,a} + p_{c}^{n-1} * P_{c,a} + p_{d}^{n-1} * P_{d,a})*d + \frac{1-d}{N}
\]

物理意义也很好了解，原先从别的网页通过链接点击过来的是有一定概率的，概率就是d。而从任意一个网页随机访问而来的概率是1/N，还要乘以1-d 。

因此

\[W_{n} = d * W_{n-1} \cdot P + \frac{1-d}{N}
\]

修改一下程序，再运行一下

转移矩阵:
0.000 0.000 0.000 0.000
0.500 0.000 0.500 0.000
1.000 0.000 0.000 0.000
0.333 0.333 0.333 0.000 

初始状态:
0.250 0.250 0.250 0.250
状态1 :
0.675 0.250 0.463 0.038 

状态2 :
0.675 0.069 0.282 0.038 

状态3 :
0.368 0.069 0.128 0.038 

状态4 :
0.237 0.069 0.128 0.038 

状态5 :
0.237 0.069 0.128 0.038

最终四个网页的权重再第五步的时候就收敛了，可以看到A网页的权重是最高的，因为它被指向的链接是最多的。

我对 PageRank 算法的初步了解就这么多了，我觉得PageRank 也应该算是马尔科夫链的应用之一吧。

参考链接：

维基百科 ：https://zh.wikipedia.org/wiki/PageRank

LDA 数学八卦 PDF： http://bloglxm.oss-cn-beijing.aliyuncs.com/lda-LDA数学八卦.pdf