数值计算方法实验之Lagrange 多项式插值 (Python 代码)

一、实验目的

在已知f(x),x∈[a,b]的表达式，但函数值不便计算,或不知f(x),x∈[a,b]而又需要给出其在[a,b]上的值时，按插值原则f(x_i)= y_i(i= 0,1…….,n)求出简单函数P(x)(常是多项式),使其在插值基点x_i,处成立P(x_i)= y_i(i=0,1,……,n),而在[a,b]上的其它点处成立f(x)≈P(x).

二、实验原理

三、实验内容

求之f(x)=x⁴在[0,2]上按5个等距节点确定的Lagrange插值多项式.

四、实验程序

 import matplotlib.pyplot as plt
 from pylab import mpl

 #计算插值多项式的系数。
 x = [0, 0.5, 1, 1.5, 2]
 y = [0, 0.0625, 1, 5.0625, 16]

 def ParametersOfLagrangeInterpolation(data_x,data_y,size):
     parameters=[]

     i=0;#i用来控制参数的个数
     while i < size:
         j = 0;#j用来控制循环的变量做累乘
         temp = 1;
         while j < size:
             if(i != j):
                 temp*=data_x[i]-data_x[j]
             j+=1;
         parameters.append(data_y[i]/temp)
         i += 1;
     return parameters

 #计算拉格朗日插值公式的值。

 def CalculateTheValueOfLarangeInterpolation(data_x,parameters,x):
     returnValue=0
     i = 0;
     while i < len(parameters):
         temp = 1
         j = 0;
         while j< len(parameters):
             if(i!=j):
                 temp *=x-data_x[j]
             j+=1
         returnValue += temp * parameters[i]
         i += 1
     return returnValue

 #将函数绘制成图像
 def  Draw(data_x,data_y,new_data_x,new_data_y):
         plt.plot(new_data_x, new_data_y, label="拟合曲线", color="red")
         plt.scatter(data_x,data_y, label="离散数据",color="yellow")
         plt.scatter(1.75, 9.37890625, label="真实数据", color="orange")
         plt.scatter(1.25, 2.44140625, color="green")
         mpl.rcParams['font.sans-serif'] = ['SimHei']
         mpl.rcParams['axes.unicode_minus'] = False
         plt.title("Lagrange插值拟合数据")
         plt.legend(loc="upper left")
         plt.show()

 parameters=ParametersOfLagrangeInterpolation(x,y,5)
 datax=[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2]
 datay=[]
 for temp in datax:
     datay.append(CalculateTheValueOfLarangeInterpolation(x,parameters,temp))
 x.append(1.75)
 y.append(CalculateTheValueOfLarangeInterpolation(x,parameters,1.75))
 Draw(x,y,datax,datay)
 print("得到的四次Lagrange插值多项式为：L(x) = %f(x-0)(x-1)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1)(x-2) + %f(x-0)(x-0.5)(x-1)(x-1.5)"%(parameters[1],parameters[2],parameters[3],parameters[4]))

五、运算结果

(1)图像

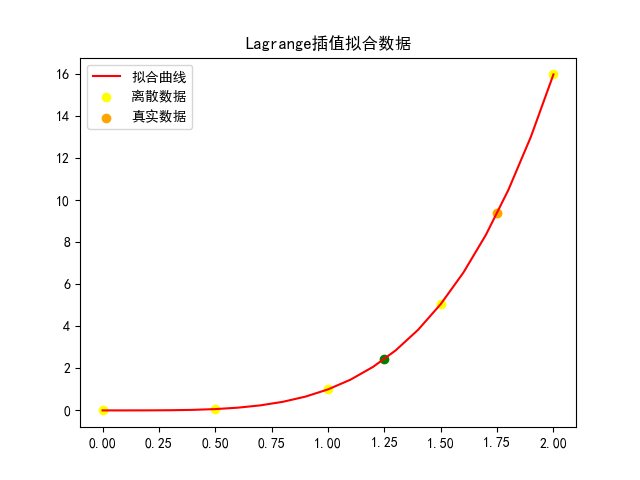
(2)运算结果

得到的四次Lagrange插值多项式为：L(x) = -0.166667(x-0)(x-1)(x-1.5)(x-2) + 4.000000(x-0)(x-0.5)(x-1.5)(x-2) + -13.500000(x-0)(x-0.5)(x-1)(x-2) + 10.666667(x-0)(x-0.5)(x-1)(x-1.5)