方差分析||MSA/MSE|
应用统计学-方差分析
数值型数据使用线性回归来研究因素对因变量的影响。类别型数据使用方差分析来研究因素对因变量的影响。方差分析是使用方差比MSA/MSE来检验均值是否全相等,即相等是H0假设,而不全相等是H1假设。
自变量是因素,而因素取值是水平。比如,降水量是因素,降水量大、中和小是因素的三个水平。
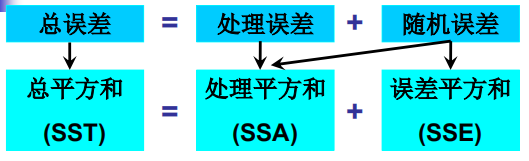
看方差是否相等,来判断组间差异是不是很大,
组内组间都有随机误差,但是不是一种随机误差
方差分析||MSA/MSE|的更多相关文章
- 方差分析|残差|MSA/MSE|Completely randomized design|Randomized block design|LSD|主效应|intercept|多重比较|
符合方差分析的三个条件: 残差=实际值-预测值(其实是均值). 在原假设下,MSA的期望会等于MSE的期望:在备选假设下,MSA的期望会大于MSE的期望,所以MSA/MSE的取值范围在(1,正无穷), ...
- 方差分析(python代码实现)
python机器学习-乳腺癌细胞挖掘(欢迎关注博主主页,学习python视频资源,还有大量免费python经典文章) https://study.163.com/course/introduction ...
- 用Python学分析 - 单因素方差分析
单因素方差分析(One-Way Analysis of Variance) 判断控制变量是否对观测变量产生了显著影响 分析步骤 1. 建立检验假设 - H0:不同因子水平间的均值无差异 - H1:不同 ...
- 多重检验_LSD方法不准确性
sklearn实战-乳腺癌细胞数据挖掘(博客主亲自录制视频教程) https://study.163.com/course/introduction.htm?courseId=1005269003&a ...
- 主效应|处理误差 |组间误差|处理效应|随机误差|组内误差|误差|效应分析|方差齐性检验|SSE|SSA|SST|MSE|MSA|F检验|关系系数|完全随机化设计|区组设计|析因分析
8 什么是只考虑主效应的方差分析? 就是不考虑交互效应的方差分析,即认为因素之间是不相互影响的,就是无重复的方差分析. 什么是处理误差 (treatment error).组间误差(between ...
- Atitit 软件架构方法的进化与演进cs bs soa roa msa attilax总结
Atitit 软件架构方法的进化与演进cs bs soa roa msa attilax总结 1.1. 软件体系架构是沿着单机到 CS 架构,再到 BS 的三层架构甚至多层架构逐步发展过来的,关于 ...
- Hotelling T2检验和多元方差分析
1.1 Hotelling T2检验 Hotelling T2检验是一种常用多变量检验方法,是单变量检验的自然推广,常用于两组均向量的比较. 设两个含量分析为n,m的样本来自具有公共协方差阵的q维正态 ...
- 方差分析 ANOVA
来源: http://blog.sciencenet.cn/blog-479412-391481.html 方差分析是为了比较多个总体样本均数是否存在差别.该方法有RA.Fisher首先提出,后来由G ...
- MSA:多重比对序列的格式及其应用
多重比对序列的格式及其应用 这里对多重序列比对格式(Multiple sequence alignment – MSA)进行总结.在做系统演化分析.序列功能分析.基因预测等,都需要涉及到多重序列比 ...
随机推荐
- (转)绝对路径${pageContext.request.contextPath}用法及其与web.xml中Servlet的url-pattern匹配过程
以系统的一个“添加商品”的功能为例加以说明,系统页面为add.jsp,如图一所示: 图一 添加商品界面 系统的代码目录结构及add.jsp代码如图二所示: 图二 系统的代码目录结构及add.js ...
- centos7-vsftp(虚拟用户)
要求如下: 1.所有用户主目录为/var/www宿主为virtual用户: 2.ftpuser1用户只能下载不能上传以及删除文件重命名操作: 3.ftpuser2可以下载与上传文件以及删除重命名操作: ...
- F5 BIG-IPLTM但比组网的三种连接模式(转)
原文链接:https://www.cnblogs.com/yujianadu/p/11850977.html作者:遇见阿杜
- B. Odd Sum Segments CF(分割数组)
题目地址 http://codeforces.com/contest/1196/problem/B B. Odd Sum Segments time limit per test 3 seconds ...
- 关于阿里云的远程连接和轻型桌面(xfce4)安装
这里用的阿里云服务器是轻量应用服务器 先通过网页端的远程连接进入服务器,然后 安装xfce4 (1)先安装更新:apt-get update. (2)安装xrdp:输入apt-get install ...
- 理解浮动和position定位(转)
前言 为了更好理解浮动和position,建议先看看我写的这篇文章<Html文档流和文档对象模型DOM理解> 正文 一.浮动 CSS设计float属性的主要目的,是为了实现文本绕排图片的效 ...
- 深入理解JVM - JVM内存模型
各版本的差异 JDK1.6 在JDK1.6 的时候运行时常量池在方法区中 JDK1.7 在JDK1.7 的时候运行时常量池在堆中 JDK1.8 在JDK1.8 的时候,JVM内存模型直接将方法区移到了 ...
- Kattis dragonball1 Dragon Ball I(最短路)
There is a legendary tale about Dragon Balls on Planet X: if one collects seven Dragon Balls, the Dr ...
- ae基础一
1.导入素材2.整理素材3.创建合成1280*720是高清的模式 也是平时都用的格式 HDV/HDTV 720 251920*1080是超清的模式格式是以16:9的格式显示的 电脑电视机都是用这个比例 ...
- sphinx转pdf显示中文
在conf.py中 修改, 加入 ctex包 latex_elements = { # The paper size ('letterpaper' or 'a4paper'). #'papersize ...
