最短路算法之Dijkstra算法通俗解释

Dijkstra算法

---

说明：求解从起点到任意点的最短距离，注意该算法应用于没有负边的图。

来，看图。

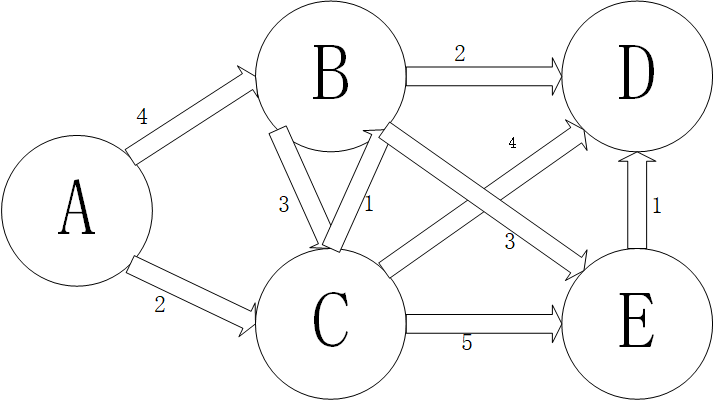
用邻接矩阵表示

       int[][] m = {
                {0, 0, 0, 0, 0, 0},
                {0, 0, 4, 2, 0, 0},
                {0, 0, 0, 3, 2, 3},
                {0, 0, 1, 0, 4, 5},
                {0, 0, 0, 0, 0, 0},
                {0, 0, 0, 0, 1, 0}};

备注：第一行（从第零行开始）表示A，第一列（从第零列开始）表示A。m[1][2]表示A到B的距离，如果没有相连则赋值为0。

首先用dist[i]数组表示从起点到该点的距离，比如dist[3]表示起点A到点C的距离。先全部初始化为无穷大，把起点初始化为0，因为自己到自己距离为0。接下来把所有的点的距离放入一个优先队列。步骤：

遍历直到队列为空：

在优先队列中删除值（dist[i]）最小的点，不过记得保存下来，然后看与其相邻的点的距离，如果相邻的点的距离大于该点距离加上该点到相邻点的距离，则改变相邻的点的距离为该点距离加上该点到相邻点的距离，在优先队列中改变这个相邻的点的距离就好了。

解释：就是宽度优先搜索的变形，宽度优先搜索是直接从队列取出来就好了，没有优先顺序，而这个是根据该点的距离值（就是从起点到该点的距离）来确定优先出队顺序。

在这里优先队列实现的方案有四种：数组，二分堆，d堆，Fibonacci堆。复杂度可以自己去分析一下。提示：你可以计算从队列中删除和加入，复杂度分别是多少，就很容易算出来了。在这里说下数组的吧，从数组中删除最小的：o(V)，插入：o(1)，总：o(v^2)

来，看下我的代码实现。我是用的map，复杂度与数组实现类似。

import java.util.*;

public class Main {

    public static int deleteMin(Map<Integer, Integer> map) {
        int min = Integer.MAX_VALUE;
        for (int num : map.values()) {
            min = Math.min(min, num);
        }
        int u = 0;
        for (int num : map.keySet()) {
            if (map.get(num) == min) {
                u = num;
                break;
            }
        }
        map.remove(u);
        return u;
    }

    public static void dijkstra(int[][] m) {
        int n = m.length;
        int[] dist = new int[n + 1];
        int[] pre = new int[n + 1];
        for (int i = 0; i < n; i++) dist[i] = Integer.MAX_VALUE;
        dist[1] = 0;
        pre[1] = 1;
        //点与距离
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 1; i < n; i++) {
            map.put(i, dist[i]);
        }
        while (!map.isEmpty()) {
            int u = deleteMin(map);
            for (int i = 1; i < n; i++) {
                if (m[u][i] > 0) {
                    if (dist[i] > dist[u] + m[u][i]) {
                        dist[i] = dist[u] + m[u][i];
                        pre[i] = u;
                        map.put(i, dist[i]);
                    }
                }
            }
        }
        for (int i = 1; i < n; i++) {
            System.out.println("节点1离节点" + i + "距离是：" + dist[i] + "，节点" + i +"的父节点是；" + pre[i]);
        }
    }

    public static void main(String[] args) {
        int[][] m = {
                {0, 0, 0, 0, 0, 0},
                {0, 0, 4, 2, 0, 0},
                {0, 0, 0, 3, 2, 3},
                {0, 0, 1, 0, 4, 5},
                {0, 0, 0, 0, 0, 0},
                {0, 0, 0, 0, 1, 0}};
        dijkstra(m);

    }

}