从交叉熵损失到Facal Loss

1交叉熵损失函数的由来
1.1关于熵，交叉熵，相对熵（KL散度）
　　熵：香农信息量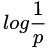的期望。变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。其计算公式如下：

　　　　

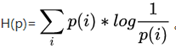
　　其是一个期望的计算，也是记录随机事件结果的平均编码长度(关于编码：一个事件结果的出现概率越低，对其编码的bit长度就越长。即无法压缩的表达，代表了真正的信息量.)
熵与交叉熵之间的联系：
　　假设有两个分布p,q。其中p是真实概率分布,q是你以为（估计）的概率分布（可能不一致）；你以 q 去编码,编码方案 log(1/qi)可能不是最优的； 于是,平均编码长度 = ∑pi *log(1/qi),就是交叉熵；只有在估算的分布q完全正确时，即q与p的分布完全相同时，平均编码长度才是最短的，此时交叉熵 = 熵
　　相对熵: q得到的平均编码长度比由p得到的平均编码长度多出的bit数(交叉熵与熵的差值)。

　　　　　　　

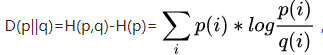
1.2交叉熵与极大似然估计得关系
　　一般情况下的极大似然函数如下：

　　　　　　　　

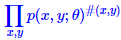
　　其中，#(x,y),表示x,y同时出现的次数。P表示概率。
　　其相对应的对数损失为：

　　　　　　

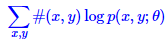
　　易知道，#(x,y)可以用样本统计频率来代替;

　　　　　　 ，

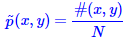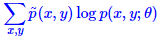
　　在前面加负号，即可变成极小问题：

　　　　　　

　　上式类似于交叉熵损失函数。也就是说，求最大似然函数的最大值，等价于求交叉熵的最小值。
1.3交叉熵损失函数特点：
　　非负性。（所以我们的目标就是最小化代价函数）
　　当真实输出a与期望输出y接近的时候，代价函数接近于0.(比如y=0，a～0；y=1，a~1时，代价函数都接近0)。
　　克服方差代价函数更新权重过慢的问题：

　　　　　　 ，

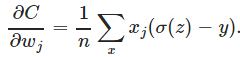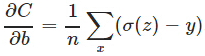
　　导数中没有σ′(z)这一项，权重的更新是受σ(z)−y这一项影响，即受误差的影响。所以当误差大的时候，权重更新就快，当误差小的时候，权重的更新就慢。
2.修正的交叉熵损失
　　考虑这样一个问题：我们的目标是极小化交叉熵损失函数。但我们最后的评估目标，并非要看交叉熵有多小，而是看模型的准确率。一般来说，交叉熵很小，准确率也会很高，但这个关系并非必然的。
　　打个比方，平均分和及格率的问题：最终的考核目标是及格率。两组数据：两个人分别考40和90，那么平均分就是65，及格率只有50%；另有两个人的成绩都是60，平均分就是60，及格率却有100%。这也就是说，平均分可以作为一个目标，但这个目标并不直接跟考核目标挂钩。这里的平均分相当于交叉熵的值，及格率相当于分类的准能率。
　　在实际的样本中，每个样本的向标签收敛的速度，难易是不同的。这些收敛难的样本我们称为为Hard Example。分类问题，我们认为大于0.5的就是正样本了，小于0.5的就是负样本。对于上述问题，一个简单的方法是：设定一个阈值为0.6，那么模型对某个正样本的输出大于0.6以及对某个负样本的输出小于0.4，我就不根据这个样本来更新模型而且了，模型，我也不根据这个样本来更新模型了，只有在0.4~0.6之间的，才让模型更新，这时候模型会更“集中精力”去关心那些“模凌两可”的样本，从而使得分类效果更好，这有点类似于传统的SVM思想是一致的。
2.1硬截断
　　硬截断Loss的形式为:

　　　　 　　

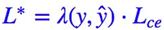
　　其中：

　　　　　 

　　正样本的预测值大于 0.5 的，或者负样本的预测值小于 0.5 的，我都不更新了，把注意力集中在预测不准的那些样本，当然这个阈值可以调整。这样做能部分地达到目的，但是所需要的迭代次数会大大增加。
　　原因是这样的：对于正确分类且满足条件的样本，其梯度为0.，相当于没有这些样本，下一阶段的计算只有分类错误的样本起作用。分类规则会一直向分类错误样本方向移动，所以在之后的某一阶段，之前分类正确的预测值就很有可能变回小于 0.5 了。（这里的0.5是一个阈值，并没有特殊的含义，可以根据情况自行更改）。
2.2软截断
　　硬截断会出现不足，关键地方在于因子 λ(y,ŷ) 是不可导的，或者说我们认为它导数为 0，因此这一项不会对梯度有任何帮助。避免这种情况的一种方法是光滑化Loss。
　　根据λ定义，可以发现其性质与sigmoid函数性质一致，所以可以用sigmoid函数近似λ函数。更改后的Loss函数为： 　　　　　　　　　　　　　　　

　　　　　　

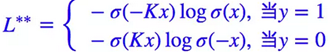
　　其中theat函数为sigmoid函数，K的作用是使theat函数近似于0.

　　　　　　

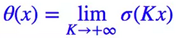
　　其中， 和 为超参数。

3. Fcal Loss
3.1. 来源
　　该损失函数是在Kaiming He的一篇论文中提出的。动机如下：图像目标检测框架主要有两种：一种是 one-stage ，例如 YOLO、SSD 等，这一类方法速度很快，但识别精度没有 two-stage 的高，其中一个很重要的原因是，利用一个分类器很难既把负样本抑制掉，又把目标分类好。另外一种目标检测框架是 two-stage ，以 Faster RCNN 为代表，这一类方法识别准确度和定位精度都很高，但存在着计算效率低，资源占用大的问题。Focal Loss 从优化函数的角度上来解决这些问题，使得在能够匹配以前的一级探测器的速度同时超过所有现有最先进的两级探测器的精度。实验结果非常 solid，很赞的工作。
　　论文认为训练过程中阻碍单阶段检测器精度不高的主要障碍是类别失衡，并提出了一种新的损失函数来消除这个障碍。sliding window的工作方式会使正负样本接近1000：1，而且绝大部分负样本都是easy example。往往这些easy example虽然loss很低，但由于数量众多，对于loss依旧有很大贡献（使得训练一直向这些easy example的方向移动），从而导致收敛到不够好的一个结果。
3.2. 函数形式
　　　　　　

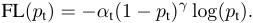
　　上式和软截断损失函数中对数前面的系数的作用是一样的，都是为了降低分类正确样本对于训练的贡献。只不过一个是指数方式，一个是sigmoid变化方式。K和 的作用都是一样的，都是调节权重曲线的陡度。
　　另外，其中也体现了对不均衡样本的解决方法。以二分类为例：当负样本远比正样本多的话，模型肯定会倾向于数目多的负类（可以想象全部样本都判为负类），这时候，负类的 或 都很小，而相应的正类的就很大，这时候模型就会开始集中精力关注正样本。
3.3. 实现
　　

　　　　

论文原文：
　　Lin T Y, Goyal P, Girshick R, K He，P Dollárl. Focal Loss for Dense Object Detection[J]. 2017.
　　https://www.zhihu.com/question/41252833
　　http://blog.csdn.net/u014313009/article/details/51043064