C语言实现二叉树的基本操作

二叉树是一种非常重要的数据结构。本文总结了二叉树的常见操作：二叉树的构建，查找，删除，二叉树的遍历(包括前序遍历、中序遍历、后序遍历、层次遍历)，二叉搜索树的构造等。

1. 二叉树的构建

  二叉树的基本构建方式为:添加一个节点，如果这是一棵空树，则将该节点作为根节点；否则按照从左到右、先左子树后右子树的顺序逐个添加节点。比如依次添加节点:1,6,10,2,7,11，则得到的二叉树为:



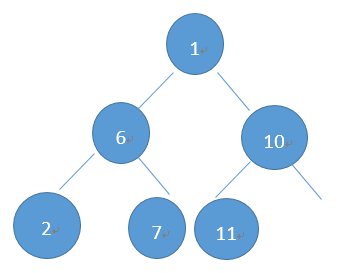
在这里，我们需要借助一个链表来保存节点，以实现二叉树的顺序插入，具体做法如下：

1.0 初始化一个用来保存二叉树节点的空链表；

1.1 插入一个节点，

①如果该树是一棵空树，则将该节点作为根节点，并且将该节点添加到链表中；

②如果该树不为空，取得链表第一个节点的值(注意不是链表的头节点)。如果该节点左子树为空，则将待插入节点添加到左子树，并且将左子树添加到链表；否则将待插入节点添加到右子树，将右子树添加到链表。此时，父节点的左右子树都不为空，将该父节点(即链表第一个节点)

弹出。

按照这样的顺序，我们就可以完成二叉树节点的顺序插入。

2. 二叉搜索树的构建

   二叉搜索树是这样一棵树：对于任意一个节点，其左子树的值均小于父节点的值；右子树的值均大于父节点的值。从二叉树的根节点开始，对于其左右子树均按照这样的方式递归插入，即可以得到一棵二叉搜索树。二叉搜索树具有很好的性质，因为它的有序性，如果在二叉搜索树中查找一个元素可以按照类似二分查找的方式进行；对于二叉搜索树，如果采用中序遍历则可以得到按照值递增排列的节点。二叉搜索树的具体构建方式如下：

插入一个节点：

2.1如果当前节点本身值为空，则将插入节点直接作为当前节点；

2.2如果当前节点本身值不为空，

①比较插入节点的值与当前节点的值，如果插入节点值小于当前节点值，则将该节点递归插入左子树；

②比较插入节点的值与当前节点的值，如果插入节点值大于当前节点值，则将该节点递归插入右子树；

③ 如果插入节点的值等于当前节点的值，则直接返回(即二叉搜索树每个节点的值都是不同的)。

3.二叉搜索树的查找

  二叉搜索树的查找类似于二分查找。具体步骤如下：

3.1 从根节点开始，比较查找值与当前节点值的大小：

① 如果当前节点值为空，则说明无法查找到该值，直接返回；

②如果当前节点值等于查找值，则查找成功；

③如果查找值小于当前节点的值，则递归查找左子树；

④如果查找值大于当前节点的值，则递归查找右子树。

4. 二叉搜索树的删除

   二叉搜索树的删除与查找基本类似，不同之处在于如果查找到了待删除的节点，则将该节点直接删除之后，还要进行如下操作保证删除节点之后的二叉树仍是一棵二叉搜索树：

①如果该删除节点没有左右子树，则直接删除该节点；

②如果该删除节点只有左子树(右子树)，则将删除节点的父节点直接指向其左子树(右子树);

③如果该删除节点既有左子树又有右子树，则有下面的三种处理方法：

4.3.1：找到按照中序遍历该删除节点的直接前驱节点，将该节点转移到删除节点，然后删除这个前驱节点；

4.3.2：找到按照中序遍历该删除节点的直接后续节点，将该节点转移到删除节点，然后删除这个后序节点；

4.3.3：找到按照中序遍历该删除节点的直接前驱节点，将删除节点的左子树接到父节点上，将删除节点的右子树接到该前序节点的右子树上，然后删除节点。

5. 二叉树的前序遍历

  由于二叉树是递归定义的，所以二叉树的遍历一般也是采用递归的形式。前序遍历即采用先访问根节点，再访问左子树，最后访问右子树的顺序。前序遍历也是按照类似的方式递归遍历，具体操作如下：

① 如果当前节点值为空，返回；

②如果当前节点值不为空，打印当前节点值；递归遍历左子树；递归遍历右子树。

6. 二叉树的中序遍历

①如果当前节点值为空，返回；

②递归遍历左子树；打印当前节点的值；递归遍历右子树。

7. 二叉树的后序遍历

①如果当前节点值为空，返回；

②递归遍历左子树；递归遍历右子树；打印当前节点的值。

8. 二叉树的层次遍历

  二叉树的层次遍历，即从根节点开始，逐层按照从左到右的顺序遍历。层次遍历比前中后序遍历要麻烦一点，它需要借助一个额外的链表来保存节点进行遍历。具体做法如下：

①初始化一个用来保存二叉树节点的空链表；

②如果这是一棵空二叉树，直接返回；否则将根节点添加到链表；

③while(当链表不为空时)

  弹出链表第一个二叉树节点，打印该二叉树节点的值；

  如果该二叉树节点的左子树不为空，则将该左子树添加到链表；

  如果该二叉树节点的右子树不为空，则将该右子树添加到链表；

  以上就是关于二叉树的基本操作，下面是C语言具体实现的代码，供大家参考：

/*
二叉树的基本操作:插入，删除,查找,前序遍历,中序遍历,后序遍历,层次遍历
*/
#include<stdio.h>
#include<stdlib.h>
#define BLANK -1
#define LEFT -2
#define RIGHT -3
typedef struct BINARY_TREE
{
	// 左子树
	struct BINARY_TREE *left;
	// 右子树
	struct BINARY_TREE *right;
	int value;
} Binary_tree;
typedef struct NODE
{
	struct NODE *link;
	Binary_tree *value;
} Node;

// 二叉树插入
int insert(Binary_tree *root,int value,Node *node_root);
// 二叉搜索树插入
int search_insert(Binary_tree *root,int value);
// 二叉树删除
int erase(Binary_tree *roote,int value);
// 二叉搜索树查找
int search_find(Binary_tree *root,int value);
// 二叉树前序遍历
void pre_print(Binary_tree *root);
// 二叉树中序遍历
void mid_print(Binary_tree *root);
// 二叉树后序遍历
void back_print(Binary_tree *root);
// 层次遍历
void level_print(Binary_tree *root);
// 弹出链表第一个元素
Binary_tree* top(Node *root);
// 将元素添加到链表末尾
int append(Node *current,Binary_tree* value);

int main(void)
{
	Binary_tree *root = (Binary_tree*)malloc(sizeof(Binary_tree));
	if(root == NULL)
	{
		printf("Malloc memory failed!\n");
		exit(-1);
	}
	root->left = NULL;
	root->right = NULL;
	root->value = BLANK;
	Node *node_root = (Node*)malloc(sizeof(Node));
	if(node_root == NULL)
	{
		printf("Malloc memory failed!\n");
		exit(-1);
	}
	node_root->link = NULL;
	search_insert(root,10);
	search_insert(root,2);
	search_insert(root,2);
	search_insert(root,3);
	search_insert(root,4);
	search_insert(root,15);
	search_insert(root,6);
	search_find(root,15);
        /*
	insert(root,10,node_root);
	insert(root,2,node_root);
	insert(root,2,node_root);
	insert(root,3,node_root);
	insert(root,4,node_root);
	insert(root,15,node_root);
	insert(root,6,node_root);
	*/
	printf("前序遍历: ");
	pre_print(root);
	puts("");
	printf("中序遍历: ");
	mid_print(root);
	puts("");
	printf("后序遍历: ");
	back_print(root);
	puts("");
	printf("层次遍历: ");
	level_print(root);
	puts("");
	free(root);
	return 0;
}
// 二叉树插入
int insert(Binary_tree *root,int value,Node *node_root)
{
	// 如果是空树
	if(root->left == NULL && root->right == NULL && root->value == BLANK)
	{
		root->value = value;
		append(node_root,root);
		printf("Insert %d into an empty link list!\n",value);
	}
	else
	{
		// 构造一个新节点
		Binary_tree *new_tree_node = (Binary_tree*)malloc(sizeof(Binary_tree));
		new_tree_node->value = value;
		new_tree_node->left = new_tree_node->right = NULL;
		// 得到链表第一个节点的值
		Binary_tree *current = node_root->link->value;
		// 如果左子树为空
		if(current->left == NULL)
		{
			current->left = new_tree_node;
			append(node_root,current->left);
			printf("Insert %d in parent's left node!\n",value);
		}
		// 左子树不为空
		else
		{
			current->right = new_tree_node;
			append(node_root,current->right);
			printf("Insert %d in parent's right node!\n",value);
			top(node_root);
		}
	}
	return 0;
}
// 二叉搜索树插入
int search_insert(Binary_tree *root,int value)
{
	// 如果左右子树都为空且根节点值为小于0(BLANK 或者 LEFT 或者 RIGHT)
	if(root->left == NULL && root->right == NULL && root->value < 0)
	{
		if(root->value == BLANK)
			printf("Insert %d into an empty binary tree succeed!\n",value);
		else if(root->value == LEFT)
			printf("Insert %d into parent's left node succeed!\n",value);
		else
			printf("Insert %d into parent's right node succeed!\n",value);
		root->value = value;
		return value;
	}
	if(value < root->value)
	{
		if(root->left == NULL)
		{
			root->left = (Binary_tree*)malloc(sizeof(Binary_tree));
			if(root->left == NULL)
			{
				printf("Malloc memory failed!\n");
				exit(-1);
			}
			root->left->value = LEFT;
			root->left->left = root->left->right = NULL;
		}
		search_insert(root->left,value);
	}
	else if(value > root->value)
	{
		if(root->right == NULL)
		{
			root->right = (Binary_tree*)malloc(sizeof(Binary_tree));
			if(root->right == NULL)
			{
				printf("Malloc memory failed!\n");
				exit(-1);
			}
			root->right->value = RIGHT;
			root->right->left = root->right->right = NULL;
		}
		search_insert(root->right,value);
	}
	else
	{
		printf("%d already exits in binary tree!\n");
		return value;
	}
}

// 二叉搜索树查找
int search_find(Binary_tree *root,int value)
{
	if(root->left == NULL && root->right == NULL && root->value < 0)
	{
		printf("Can't find %d in binary tree!\n",value);
		return -1;
	}
	if(root->value == value)
	{
		printf("Find %d in binary tree!\n",value);
		return 0;
	}
	else if(value < root->value)
	{
		if(root->left == NULL)
		{
			printf("Can't find %d in binary tree!\n",value);
			return -1;
		}
		search_find(root->left,value);
	}

	else
	{
		if(root->right == NULL)
		{
			printf("Can't find %d in binary tree!\n",value);
			return -1;
		}
		search_find(root->right,value);
	}
}
// 二叉树前序遍历
void pre_print(Binary_tree *root)
{
	if(root->left == NULL && root->right == NULL && root->value < 0)
		return;
	printf("%d ",root->value);
	if(root->left != NULL)
		pre_print(root->left);
	if(root->right != NULL)
		pre_print(root->right);
}

// 二叉树中序遍历
void mid_print(Binary_tree *root)
{
	if(root->left == NULL && root->right == NULL && root->value < 0)
		return;
	if(root->left != NULL)
		pre_print(root->left);
	printf("%d ",root->value);
	if(root->right != NULL)
		pre_print(root->right);
}

// 二叉树后序遍历
void back_print(Binary_tree *root)
{
	if(root->left == NULL && root->right == NULL && root->value < 0)
		return;
	if(root->left != NULL)
		pre_print(root->left);
	if(root->right != NULL)
		pre_print(root->right);
	printf("%d ",root->value);
}

// 弹出链表第一个元素
Binary_tree* top(Node *root)
{
	if(root->link == NULL)
	{
		printf("Can't get top value from empty link list!\n");
		exit(-1);
	}
	Node *current = root->link;
	root->link = current->link;
	return current->value;
}
// 将元素添加到链表末尾
int append(Node *current,Binary_tree* value)
{
	Node *new_node = (Node*)malloc(sizeof(Node));
	new_node->value = value;
	while(current->link != NULL)
	{
		current = current->link;
	}
	current->link = new_node;
	new_node->link = NULL;
	return 0;
}

// 二叉树层次遍历
void level_print(Binary_tree* root)
{
	if(root->left == NULL && root->right == NULL && root->value < 0)
		return;
	Node *node_root = (Node*)(malloc(sizeof(Node)));
	node_root->link = NULL;
	append(node_root,root);
	Binary_tree* current;
	while(node_root->link != NULL)
	{
		current = top(node_root);
		printf("%d ",current->value);
		if(current->left != NULL)
			append(node_root,current->left);
		if(current->right != NULL)
			append(node_root,current->right);
	}
}

运行结果如下：