cdoj913-握手 【Havel定理】

http://acm.uestc.edu.cn/#/problem/show/913

握手

Time Limit: 2000/1000MS (Java/Others)     Memory Limit: 65535/65535KB (Java/Others)

Submit Status

一群人参加了一次聚会，其中有一些人是好朋友。一对朋友见面后握手且仅握一次手，并且每个人不会和自己握手（废话！）。现在告诉你每个人一共握了几次手，请你判断是否存在一种朋友关系满足每个人的握手数。

Input

输入多组数据，第一行一个数T，表述数据组数。每组数据第一行输入一个数n，表示有n个人参加了聚会，下一行有n个数，di到dn ，di表示第i个人的握手数。 （1≤n≤105 ，输入的所有d之和不超过5×105）

Output

存在这种朋友关系输出YES，反之NO。

Sample input and output

Sample Input	Sample Output
3 3 0 1 1 3 2 2 2 3 1 1 1	YES YES NO

题解：用Havel定理解即可。

握手定理：任意图所有顶点度数之和必为偶数。

度序列：V(G)={v1,v2,....vn},称序列 {d(v1),d(v2),....d(vn)}为度序列。

一个正整数序列(d1,d2,.....,dn)是度序列当且仅当。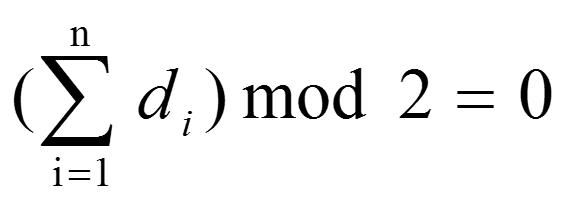

Havel定理：

一个序列：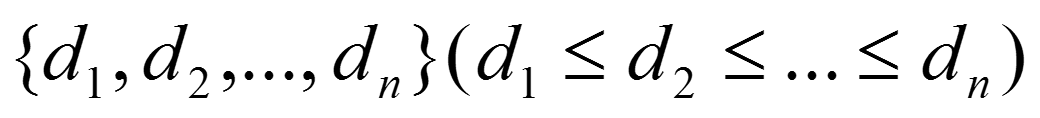

是简单图的度序列当且仅当：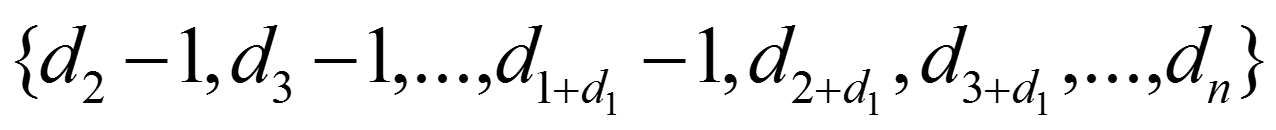

算法流程：

设序列有n个元素，d1,d2,....dn

1、若序列中出现负数则无解，若序列全为为0则有解，否则转2。

2、取出序列中最大值dmax，若dmax大于n-1,无解退出。否则取出剩下n-1个元素中前dmax大的dmax个元素，把这些元素依次减1后放回序列中，dmax舍弃，n=n-1。

代码：

 #include <fstream>
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <queue>

 using namespace std;

 const int N=;
 priority_queue<int> p;
 int n;
 int a[N],t[N];
 bool b;

 int main()
 {
     //freopen("D:\\input.in","r",stdin);
     //freopen("D:\\output.out","w",stdout);
     int T,cnt;
     scanf("%d",&T);
     while(T--){
         cnt=;
         b=;
         scanf("%d",&n);
         for(int i=;i<n;i++){
             scanf("%d",&a[i]);
             cnt+=a[i];
         }
         if(cnt&)   puts("NO");
         else{
             while(!p.empty())   p.pop();
             for(int i=;i<n;i++)    p.push(a[i]);
             while(!p.empty()){
                 cnt=p.top();
                 p.pop();
                 if(cnt>=n){
                     b=;
                     break;
                 }else if(cnt==){
                     break;
                 }
                 if(p.size()<cnt){
                     b=;
                     break;
                 }else{
                     for(int i=;i<cnt;i++){
                         t[i]=p.top()-;
                         p.pop();
                     }
                     if(t[cnt-]<){
                         b=;
                         break;
                     }
                     for(int i=;i<cnt;i++)
                         if(t[i])    p.push(t[i]);
                     n--;
                 }
             }
             if(b)   puts("YES");
             else    puts("NO");
         }
     }
     return ;
 }