[模板]LCA的倍增求法解析

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入输出格式

输入格式：

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。

接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

输出格式：

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入样例#1：

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出样例#1：

4
4
1
4
4

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

该树结构如下：

第一次询问：2、4的最近公共祖先，故为4。

第二次询问：3、2的最近公共祖先，故为4。

第三次询问：3、5的最近公共祖先，故为1。

第四次询问：1、2的最近公共祖先，故为4。

第五次询问：4、5的最近公共祖先，故为4。

故输出依次为4、4、1、4、4。

Solution:

题目来源：Luogu P3379

我们来讲讲LCA的倍增求法，来自于LS学长神犇的教授，加上我自身的理解，可能对各位新人的帮助会更有理解作用，所以我决定分享一下。（蒟蒻一本正经）

LCA——最近公共祖先。最朴素的算法无疑是从两个点一个个往上走，出现的第一个两个点都走过的点即为两点的LCA。这个无需多加解释。

然而这样时间复杂度非常高。尤其是当树退化成一条链的时候，每次查询的复杂度将会飙到O(N)。

为此，倍增的作用就是将两点上升所需的复杂度减低。而原理就是，把两点往上跳，跳到LCA.-.

流程概括为：将深度不同的两点跳到同一层（深一点的跳到浅一点的一层），然后再将两点向上跳到LCA的下面一层，最后再向上跳一层。（后面一部分下面会解释，为什么不能直接跳到LCA。）

快速跳的方法，每次向上跳的层数都为2^i层。(i为非负整数)，相当于把层数差转成2进制数，一位一位往上跳，使层数差快速减小。这样，每次查询复杂度最高就只会为log2(N)。

实现方法：

我们首先需要两个数组。f[i][j]代表从i点向上跳2^j层后所到达的点，dep[i]代表这棵树中点i的深度。

dep数组可以在从根深度遍历整棵树的时候求得。

f数组利用了递推的思想。递推式为：f[i][j]=f[f[i][j-1]][j-1]。初始化f[i][0]也可以在遍历整棵树的时候求得。

之后，我们处理LCA时，按照上面的流程。我们先将较深的点一次次往上逼近较浅的点，直至他们层数相同。（相当于把层数差的二进制一位一位减去，直至变成0）

然后，两点再同时向上逼近。i从最高位开始枚举，假设两点分别为x,y，那么能向上跳的判断式为：if f[x][i]!=f[y][i] then x=f[x][i],y=f[y][i]。翻译成人话就是如果两点向上跳了2^i层以后不到同一个点就接着往上跳。为什么这样？因为如果往上跳了2^i层，即使到了同一个点，它不一定是两点的LCA。（为什么？）

这样做，最终就会到达LCA的下面一层。随后，我们再将两点向上跳一层。LCA求得。

为什么最终会到达LCA的下面一层？

我们假设从a,b点开始，往上跳2^j层，跳到同一点。不跳。往上跳2^(j-1)层，不跳到同一点，往上跳，分别到了A'，B'。显然，这种情况是一定会存在的。

那么，从A'，B’再往上跳到原来那个决定不跳的点，显然要跳2^(j-1)层。那么，那个点有可能是LCA，也有可能不是，对吧？所以，从A'，B'往上跳到LCA所需的层数，是≤2^(j-1)的。

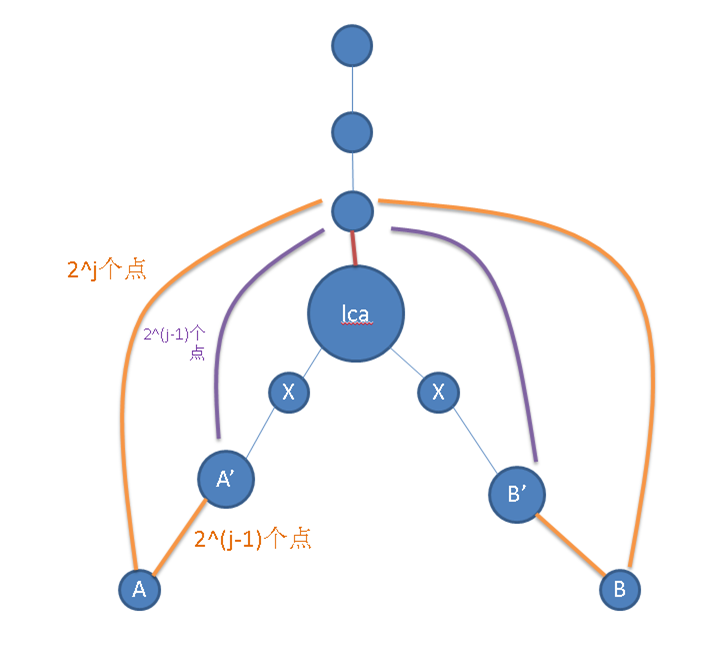
所以，从A'，B'跳到LCA的下面一层X的所需层数，会是＜2^(j-1)的。换句话来说，A'，B'到X的层数变成了一个j-2位的二进制数（可能会有前导零，也就是还可能会跳到点数相同的地方）。而此时，刚好枚举到j-2位。那么，前导零不减，再这么减下去，你发现，这个层数差最终会变成0，而你最终也会到达第X层。（为什么？）

如果不懂，也可以先放着。你只需要知道这么做可以到LCA的下面一层就OK了orz

请最好自己手画一棵树模拟一下整个算法的过程。

蒟蒻解释难免有错误，如果出现错误，请回复我，我将感激不尽orz

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=,OP=log2()+;
int dpt[N][];
int dep[N];
 
int gi(){
    int x=;
    char ch=getchar();
    while(ch<''||ch>'')ch=getchar();
    while(ch>=''&&ch<='')x=x*+ch-'',ch=getchar();
    return x;
}
 
int h[N],to[N*],nexp[N*],p=;
inline void ins(int a,int b){
    nexp[p]=h[a],h[a]=p,to[p]=b,p++;
}
 
void dfs(int p,int x){
    dep[x]=p;
    for(int u=h[x];u;u=nexp[u]){
        if(!dep[to[u]]){
            dpt[to[u]][]=x;
            dfs(p+,to[u]);
        }
    }
}
 
int LCA(int a,int b){
    if(dep[a]<dep[b])swap(a,b);
    for(int j=OP;j>=;j--)
        if(dep[a]-(<<j)>=dep[b])a=dpt[a][j];
    if(a!=b){
        for(int j=OP;j>=;j--)
            if(dpt[a][j]!=dpt[b][j])a=dpt[a][j],b=dpt[b][j];
        a=dpt[a][];
    }
    return a;
}
 
int main(){
    int n,q,r;
    cin>>n>>q>>r;
    int a,b;
    for(int i=;i<n-;i++){
        a=gi(),b=gi();
        ins(a,b),ins(b,a);
    }
    dfs(,r);
    for(int j=;j<=OP;j++)
        for(int i=;i<=n;i++)
            dpt[i][j]=dpt[dpt[i][j-]][j-];
    for(int i=;i<q;i++){
        a=gi(),b=gi();
        printf("%d\n",LCA(a,b));
    }
    return ;
}

为什么与X层数差最终会变成0？

假设你已经会写这个算法了。

首先我们证明，前导零不会被减去。假设与X层的层数差为x'，而你正准备往上跳y层。由于LCA的层数是X+1，而LCA往上的点它都不会跳，对吧？（反而，如果LCA往下的点，也就是层数<=X，也就是y<x'+1，它都会往上跳）所以如果y>=x'+1，那么就绝对不会往上跳。

显然，当x'的该位为0，且属于前导零，那么只需证明x'+1<=y。而这个非常易证（假设y为10000，而x'满足条件的最大值为01111）。所以保证，前导零是不会减去的。

接着我们证明，一旦枚举到了x'的第一个为1的位数，这个1绝对会被减去。按照同样的方法，假设y为10000，而x'满足条件的最小值为10000，所以y<x'+1.

两点合在一起，前导零不会减去，枚举到一个1位就减去，最终这个层数差就会变成0.证毕。