luoguP3830 [SHOI2012]随机树 期望概率 + 动态规划 + 结论

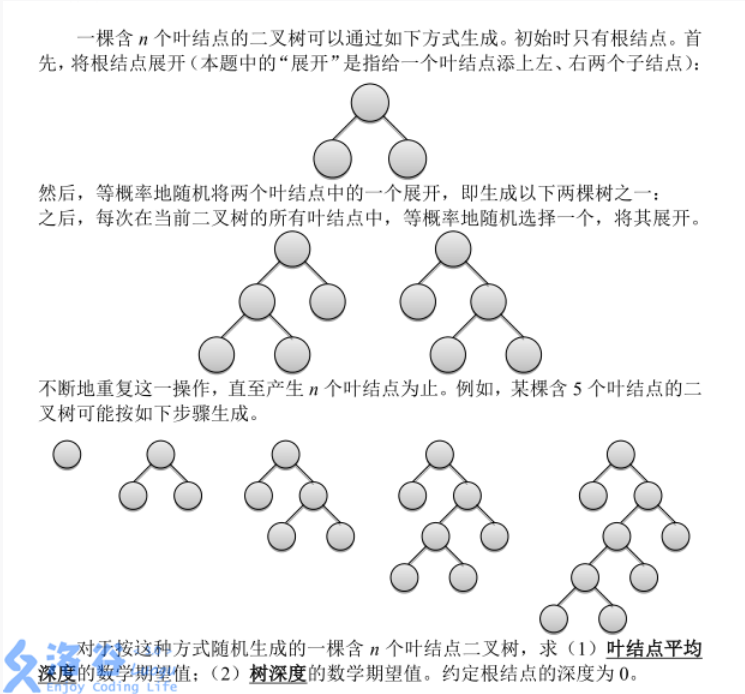
题意非常的复杂，考虑转化一下：

每次选择一个叶节点，删除本叶节点（深度为$dep$）的同时，加入两个深度为$dep + 1$的叶节点，重复$n$轮

首先考虑第$1$问，（你看我这种人相信数据绝对是最大的数据，直接$f[i][S]$表示$i$个叶子结点，深度之和为$j$的时候的概率，然后化前缀和化出来...）

对于一个深度为$x$的点，对它操作后，深度增加了$2 * (x+ 1) - x = x +2$

现在考虑平均的情况，令$f[i]$表示$i$个节点的平均深度，那么$f[i] = \frac{f[i - 1] *(i - 1) + f[i - 1] + 2}{i} = f[i - 1] + \frac{2}{i}$

其中，$f[i - 1] * (i - 1)$表示原来的总深度，$ / i$表示新的平均个数

边界为$f[1] = 0$（注意题目中深度的定义）

接着是第$2$问，考虑求解$f[i][j]$表示$i$个叶节点的树，深度为$j$的概率

那么$E(X) = \sum\limits_{i = 0}^n i * f[n][i]$

只要考虑怎么转移，自然地想到全概率公式，有

$f[i][j] = \sum\limits_{L = 1}^{i - 1} p[i][L] \sum\limits_{x = 1}^j \sum\limits_{y = 1}^j f[L][x] * f[i - L][y](x = j - 1 || y = j - 1)$

其中，$p[i][L]$表示$i$个叶子结点的树，有$L$个叶子结点落在左边的概率

同时， 注意右子树至少有$1$个叶子结点

那么，这是一个$O(n^4)$的算法

考虑进行优化，令$g[i][j] = \sum\limits_{i = 1}^j f[i][j]$

那么，现在我们的转移式变为了$f[i][j] = \sum\limits_{L = 1}^{i - 1} p[i][L] * (2 *f[L][j - 1] * g[i - L][j - 1] - f[L][j - 1] * f[i - L][j - 1])$

现在，只要求出$p[i][L]$，我们就得到了一个$O(n ^ 3)$的算法

而我们可以使用数学归纳法证明（不难）

$p[i][L] = \frac{1}{i - 1} (1 \leq L \leq i - 1)$

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

#define ri register int
#define de double
#define sid 105

int q, n;
de ans, f[sid][sid], g[sid][sid];

int main() {
    cin >> q >> n;
    if(q == ) {
        for(ri i = ; i <= n; i ++) ans += 2.0 / i;
        printf("%lf\n", ans);
    }
    else {
        f[][] = ;
        for(ri i = ; i <= n; i ++) g[][i] = f[][];
        for(ri i = ; i <= n; i ++) {
            for(ri s = ; s < i; s ++)
            for(ri L = ; L < i; L ++)
            f[i][s + ] += ( * f[L][s] * g[i - L][s] - f[L][s] * f[i - L][s]) / (i - );
            g[i][] = f[i][];
            for(ri s = ; s <= n; s ++) g[i][s] = g[i][s - ] + f[i][s];
        }
        for(ri i = ; i <= n; i ++) ans += i * f[n][i];
        printf("%lf\n", ans);
    }
    return ;
}

实际上，由于是对$E[X] = \sum\limits_{i = 1}^n i *P(X = i)$进行计数

因此，我们可以把$P(x = i)$拆成$i$份

那么，对$E[X] = \sum\limits_{i = 1}^n P(X \geq i)$计数也是可以的

然而本质没有什么改变...