sdut 2153:Clockwise（第一届山东省省赛原题，计算几何+DP）

Clockwise

Time Limit: 1000ms   Memory limit: 65536K  有疑问？点这里^_^

题目描述

Saya have a long necklace with N beads, and she signs the beads from 1 to N. Then she fixes them to the wall to show N-1 vectors – vector i starts from bead i and end up with bead i+1.

One day, Kudo comes to Saya’s home, and she sees the beads on the wall. Kudo says it is not beautiful, and let Saya make it better.

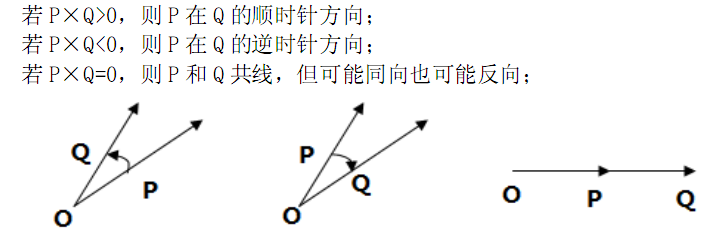
She says: “I think it will be better if it is clockwise rotation. It means that to any vector i (i < N-1), it will have the same direction with vector i+1 after clockwise rotate T degrees, while 0≤T<180.”

It is hard for Saya to reset the beads’ places, so she can only remove some beads. To saving the beads, although she agrees with Kudo’s suggestion, she thinks counterclockwise rotation is also acceptable. A counterclockwise rotation means to any vector i (i < N-1), it will have the same direction with vector i+1 after counterclockwise rotate T degrees, while 0 < T ≤ 180.”

Saya starts to compute at least how many beads she should remove to make a clockwise rotation or a counterclockwise rotation.

Since the necklace is very-very long, can you help her to solve this problem?

输入

The input consists of several test cases.
The first line of input in each test case contains one integer N (2<N≤300), which represents the number of beads.
Each of the next N lines contains two integer x and y, represents the coordinate of the beads. You can assume that 0<x,y<10000.
The last case is followed by a line containing one zero.

输出

 For each case, print your answer with the following format:
 If it is clockwise rotation without removing any beads, please print “C; otherwise if it is counterclockwise rotation without removing any beads, print “CC” instead; otherwise, suppose remove at least x beads to make a clockwise rotation and remove at least y beads to make a counterclockwise rotation. If x≤y, print “Remove x bead(s), C”, otherwise print “Removey bead(s), CC” instead.
Your output format should imitate the sample output. Print a blank line after each test case.

示例输入

3
1 1
2 2
3 3

3
1 1
2 2
1 1

4
1 1
2 2
3 3
2 2

0

示例输出

C
CC
Remove 1 bead(s), C

提示

 

来源

2010年山东省第一届ACM大学生程序设计竞赛

---

 

　　计算几何 + DP。

　　题意是给你n个点，第i个点和第i+1个点可以构成向量，问最少删除多少个点可以让构成的向量顺时针旋转或者逆时针旋转。

　　思路：

　　计算几何用的知识是求叉积和点积，这道题可以加深理解这两个计算几何基础知识点的用法。叉积的作用是判断两个向量的左右（顺逆），点积的作用是判断两个向量的前后。举个例子，假设有2个向量v1，v2，‘*’暂时代表叉积运算，‘·’暂时代表点积运算。叉积判定：如果v1*v2>0，则v1在v2的顺时针方向；如果v1*v2=0，则v1、v2共线；如果v1*v2<0，则v1在v2的逆时针方向。点积判定：如果v1·v2>0，则v1和v2都指向同一侧面；如果v1·v2=0，则v1和v2垂直；如果v1·v2<0，则v1和v2都指向相反的侧面。

　　DP是用来记录所有可能情况的最大向量数，dp[j][i]表示以向量ji（第j个点到第i个点构成的向量）为终点的最大顺时针/逆时针向量数。状态转移方程为 dp[j][i] = max{dp[k][j]+1}。

　　判断如果顺时针逆时针关系可以用叉积，如果共线再用点积判断同方向还是反方向。

 

　　注意的点：

　　1、规定顺时针的旋转范围是(0<=T<180)，逆时针的旋转范围是(0<T<=180)，也就是说如果两条向量共线的话，顺时针旋转可以同方向（T=0），不能反方向；逆时针旋转可以反方向（T=180），不能同方向。

　　2、如果删掉一定点后，顺时针旋转的最大向量数和逆时针的一样，则取顺时针的值输出。否则会WA。

　　

　　参考博客：http://blog.csdn.net/cyendra/article/details/8859274

　　代码：

 #include <iostream>
 #include <cmath>
 #include <string.h>
 using namespace std;
 #define eps 1e-10
 int dp[][];
 /********** 定义点 **********/
 struct Point{
     double x,y;
     Point(double x=,double y=):x(x),y(y) {}
 };
 Point p[];
 /********** 定义向量 **********/
 typedef Point Vector;
 /********** 点 - 点 = 向量 **********/
 Vector operator - (Point a,Point b)
 {
     return Vector(a.x-b.x,a.y-b.y);
 }
 /********** 2向量求叉积 **********/
 double Cross(Vector a,Vector b)
 {
     return a.x*b.y-b.x*a.y;
 }
 /********** 向量点积 **********/
 double Dot(Vector a,Vector b)
 {
     return a.x*b.x+a.y*b.y;
 }
 bool check1(int i,int j,int k)    //核对向量ji是否在向量kj的顺时针方向或者同方向
 {
     if(k==) return true;
     Vector v1 = p[i]-p[j];    //向量ji
     Vector v2 = p[j]-p[k];    //向量kj
     double x = Cross(v1,v2);
     if(fabs(x)<eps){    //向量ji和kj共线，判断一下两向量方向。
         double d = Dot(v1,v2);
         if(d>eps)    //顺时针可以有同方向(0≤T<180)
             return true;
         else    //反方向
             return false;
     }
     else if(x>eps){    //向量ji在向量kj的顺时针方向
         return true;
     }
     return false;
 }
 bool check2(int i,int j,int k)
 {
     if(k==) return true;
     Vector v1 = p[i]-p[j];    //向量ji
     Vector v2 = p[j]-p[k];    //向量kj
     double x = Cross(v1,v2);
     if(fabs(x)<eps){    //向量ji和kj共线，判断一下两向量方向
         double d = Dot(v1,v2);
         if(d>eps)    //同方向
             return false;
         else    //逆时针可以有反方向（0 < T ≤ 180）
             return true;
     }
     else if(x<eps){    //向量ji在向量kj的逆时针方向
         return true;
     }
     return false;
 }
 int main()
 {
     int n;
     while(cin>>n){
         if(n==) break;
         //dp[j][i]表示以向量ji（第j个点到第i个点构成的向量）为终点的最大顺时针向量数
         int i,j,k;
         for(i=;i<=n;i++)    //输入n个点
             cin>>p[i].x>>p[i].y;
         int r1=,r2=;    //最大向量数
         //dp
         memset(dp,,sizeof(dp));
         for(i=;j<=n;i++)
             for(j=;j<i;j++){
                 int Max = ;
                 for(k=;k<i;k++){
                     if(check1(i,j,k)){
                         if(dp[k][j]+>Max)
                             Max = dp[k][j]+;
                     }
                 }
                 dp[j][i]=Max;
                 if(dp[j][i]>r1)
                     r1 = dp[j][i];
             }
         memset(dp,,sizeof(dp));
         for(i=;j<=n;i++)
             for(j=;j<i;j++){
                 int Max = ;
                 for(k=;k<i;k++){
                     if(check2(i,j,k)){
                         if(dp[k][j]+>Max)
                             Max = dp[k][j]+;
                     }
                 }
                 dp[j][i]=Max;
                 if(dp[j][i]>r2)
                     r2 = dp[j][i];
             }
         if(r1==n-)    //向量数比点数少一个
             cout<<"C"<<endl;
         else if(r2==n-)
             cout<<"CC"<<endl;
         else if(r1>=r2)
             cout<<"Remove "<<n--r1<<" bead(s), C"<<endl;
         else
             cout<<"Remove "<<n--r2<<" bead(s), CC"<<endl;
         cout<<endl;
     }
     return ;
 }

Freecode : www.cnblogs.com/yym2013