[转]解读Unity中的CG编写Shader系列6——不透明度与混合

1.不透明度
当我们要将两个半透的纹理贴图到一个材质球上的时候就遇到混合的问题，由于前面的知识我们已经知道了片段着色器以及后面的环节的主要工作是输出颜色与深度到帧缓存中，所以两个纹理在每个像素上的颜色到底以怎样的形式混合在一起最后输出到帧缓存中是我们现在首要讨论的内容。

1.混合(blending)

上一篇文章中的管道环节中的“逐帧操作”环节中的一项操作就是混合操作，可见混合操作是不可编程的固定功能环节。

在混合操作中，我们将片段着色器中计算出来的颜色称之为 “源颜色”，帧缓存中对应的像素已经存在的颜色叫做“目标颜色”。混合操作就是将源颜色与目标颜色以一些选项进行结合。

既然是固定功能环节，那么这些选项我们只能选择，不能编写。

我们选择混合的选项的过程是通过以下面的等式来进行RGBA颜色的计算的:

float4 result = SrcFactor * fragment_output + DstFactor * pixel_color;

我还是用图形表达上面这个等式吧：

Unity中的Shader 通过ShaderLab语法表达的混合操作过程为：

其中这2个代号分别可以选择的选项如下表：

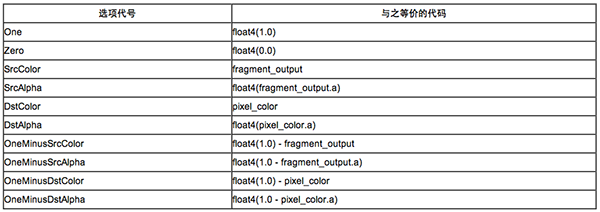
其中float4(1.0)的写法我们前面已经见过，等价于float4(1.0,1.0,1.0,1.0)

并且其中所有向量的分量区间都是[0,1]区间。
2.顺序无关的不透明度

1.加法混合