【51nod-1315】合法整数集(数位)
【思路】
既然是or操作,将数转化为二进制,数位是1,对应的数组元素+1,再将x转为成二进制,只要查找X为1的位置,将之前存放的数组数字找个最小的输出就可以了。
但是并不是所有的数都要参与or,因为有些数的位数>X,显然这些数是不用删除的,所以不用让这些数加到数组里。还有哪些数呢?当有些数的位数是1,而X对应的位数是0,这些数也是一定不用删除的。综合以上只要满足(x|xx)> x就可以参与or。
【code】
#include <bits/stdc++.h>
using namespace std;
int a[];
int main()
{
int n, m, x, c = , ans = 1e9;
cin>>n>>m;
for(int i=; i<n; i++)
{
scanf("%d", &x);
if((x|m) > m) continue;//
c = ;
while(x)
{
c++;
if(x & ) a[c]++;
x >>= ;
}
}
c = ;
while(m)
{
c++;
if(m & ) ans = min(ans, a[c]);
m >>= ;
}
printf("%d\n", ans);
return ;
}
【51nod-1315】合法整数集(数位)的更多相关文章
- 51Nod 1315 合法整数集
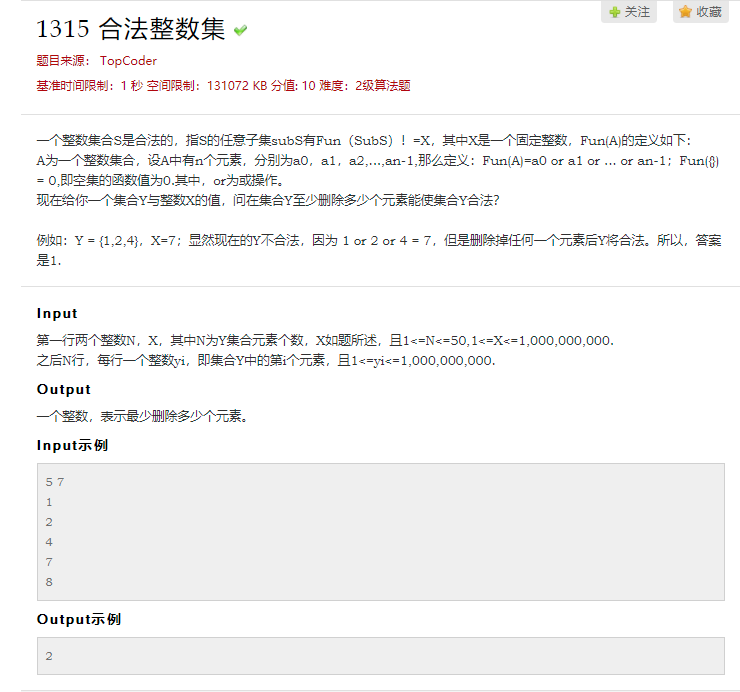
1315 合法整数集 题目来源: TopCoder 基准时间限制:1 秒 空间限制:131072 KB 分值: 10 难度:2级算法题 收藏 关注 一个整数集合S是合法的,指S的任意子集subS有Fu ...
- 疯狂位图之——位图实现12GB无重复大整数集排序
<Programming Pearls>(编程珠玑)第一章讲述了如何用位图排序无重复的数据集,整个思想很简洁,今天实践了下. 一.主要思想 位图排序的思想就是在内存中申请一块连续的空间作为 ...
- 给定一个正整数,实现一个方法求出离该整数最近的大于自身的 换位数 <把一个整数各个数位进行全排列>
"""给定一个正整数,实现一个方法求出离该整数最近的大于自身的 换位数 -> 把一个整数各个数位进行全排列""" # 使用 permu ...
- C/C++ 合法整数与字符
一.C语言中的合法整型 首先C语言中的整型有三种表示方式:十进制.八进制和十六进制.(C语言中没有表示二进制的整型) 十进制: 如 int a = 63; //一个正常的整型 八进制: 如果想用8进制 ...
- 【BZOJ2728】[HNOI2012]与非 并查集+数位DP
[BZOJ2728][HNOI2012]与非 Description Input 输入文件第一行是用空格隔开的四个正整数N,K,L和R,接下来的一行是N个非负整数A1,A2……AN,其含义如上所述. ...
- 51nod 1791 合法括号子段
有一个括号序列,现在要计算一下它有多少非空子段是合法括号序列. 合法括号序列的定义是: 1.空序列是合法括号序列. 2.如果S是合法括号序列,那么(S)是合法括号序列.3.如果A和B都是合法括号序列, ...
- 51Nod 1048 1383 整数分解为2的幂
任何正整数都能分解成2的幂,给定整数N,求N的此类划分方法的数量! 比如N = 7时,共有6种划分方法. 7=1+1+1+1+1+1+1 =1+1+1+1+1+2 =1+1+1+2+2 ...
- BZOJ2728 HNOI2012与非(并查集+数位dp)
容易发现x nand x=not x.并且使用这个性质有x and y=not(x nand y)=(x nand y)nand(x nand y).也就是说nand运算可以作为not和and运算使用 ...
- 51Nod 快速傅里叶变换题集选刷
打开51Nod全部问题页面,在右边题目分类中找到快速傅里叶变换,然后按分值排序,就是本文的题目顺序. 1.大数乘法问题 这个……板子就算了吧. 2.美妙的序列问题 长度为n的排列,且满足从中间任意位置 ...
随机推荐
- Hadoop 2.0 上深度学习的解决方案
原文连接:https://www.paypal-engineering.com/tag/data-science/ 摘要:伴随着数据的爆炸性增长和成千上万的机器集群,我们需要使算法可以适应在如此分布的 ...
- Python开篇——Python的哲学
今天奉上Python设计哲学,宣告着自己正式开始系统的学习Python The Zen of Python, by Tim Peters Beautiful is better than ugly.E ...
- Ubuntu16 安装Jira
参见:https://segmentfault.com/a/1190000008194333 https://www.ilanni.com/?p=12119烂泥:jira7.3/7.2安装.中文及破解 ...
- WCF用户名密码验证方式
WCF使用用户名密码验证 服务契约 namespace WCFUserNameConstract { [ServiceContract] public interface IWcfContract { ...
- linux之磁盘配额(quota)使用方法(转)
1.什么是quota 简单的说就是限制用户对磁盘空间的使用量. 因为Linux是多用户多任务的操作系统,许多人共用磁盘空间,为了合理的分配磁盘空间,于是就有了quota的出现. 2.quota的用途 ...
- 使用vs的时候,遇到这个:当前不会命中断点 还没有为该文档加载任何符号
一 http://stackoverflow.com/questions/2155930/fixing-the-breakpoint-will-not-currently-be-hit-no-symb ...
- UVA 1393 Highways(数学思想)
题意:给你n.m(n,m<=200),问你有多少条非水平.非垂直的直线有多少条经过至少两个点 题解:我们需要枚举的是只画一条线的矩形,对于大小a*b的矩形必须保证gcd(a,b)=1才能不重复 ...
- 【视觉基础知识】Bag of words 在图像中的应用
文章转载自:https://www.cnblogs.com/shihuajie/p/5782515.html BOW (bag of words) 模型简介 Bag of words模型最初被用在文本 ...
- Maven打包命令
mvn clean 会把原来target目录给删掉重新生成.mvn install 安装当前工程的输出文件到本地仓库,然后打包mvn clean install 先删除target文件夹 ,然后打包到 ...
- Spring boot 外部资源配置
tomcat配置访问图片路径映射到磁盘路径 首先,我在调试页面的时候发现,图片路径为: 1 /webapps/pic_son/img/1234565456.jpg 但是,tomcat中webapp ...
